HDU6610(Game 带修莫队+将区间内的值异或转化为两个前缀异或)

最新推荐文章于 2021-06-07 17:31:49 发布

Helium_wild

最新推荐文章于 2021-06-07 17:31:49 发布

阅读量341

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/qq_42576687/article/details/98211361

该博客主要介绍了如何使用带修莫队算法解决HDU6610题目的思路。题目要求在n堆石头中进行m次操作，操作包括石头位置交换，然后询问区间内石头异或值不为0的子区间数量。通过转化问题，求解等于0的子区间，利用前缀异或和进行区间匹配。在处理区间[L,R]时，需转换为[L-1,R]，并注意特殊情况如单堆石头。此外，时间复杂度优化采用了block大小为n的2/3次方。" 114742441,10554129,小学生编程挑战：随机生成加减乘除练习题,"['Java编程', '教育', '算法设计', '编程挑战', '逆波兰计算']

题目
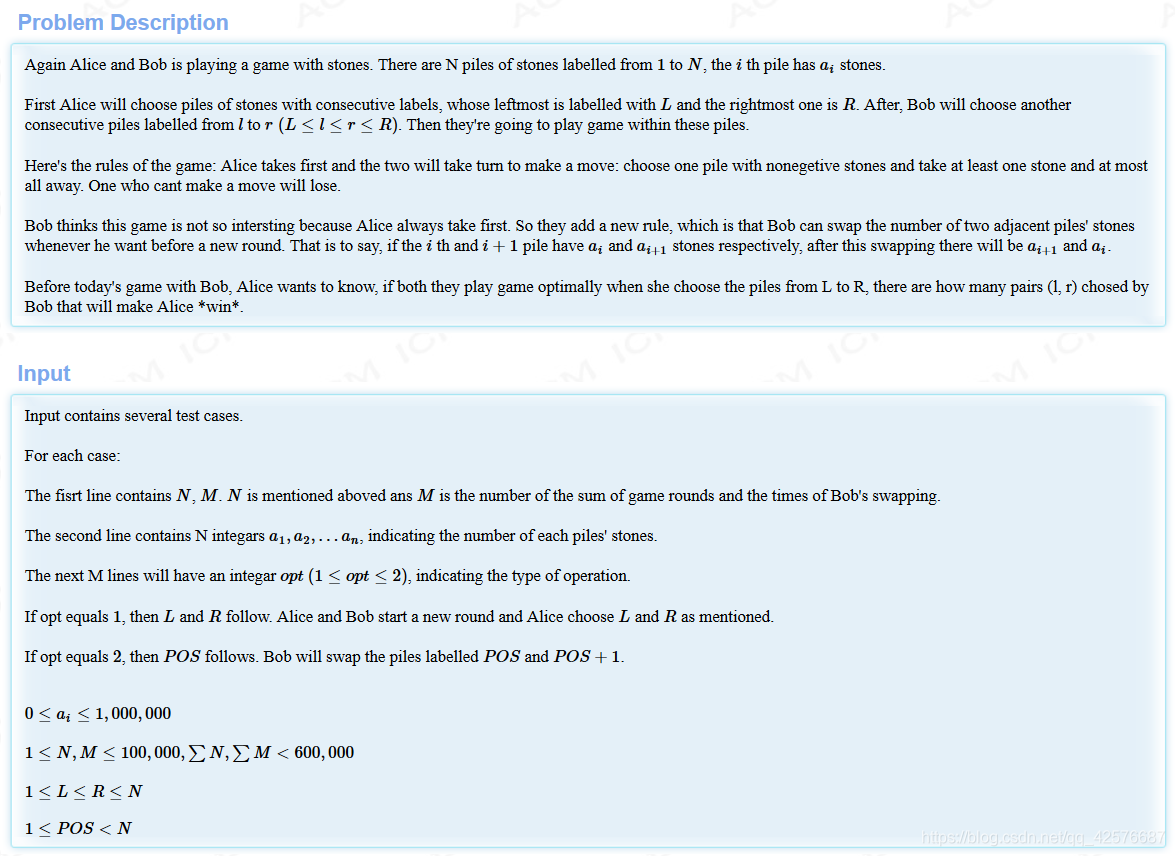
在这里插入图片描述
题意： 给你n堆石头，m次操作。操作：将x与x+1堆石头交换位置询问:[L,R]多少子区间里面的石头值异或起来不等于0.
思路： 带修莫队板子。那我们就求异或起来等于0的子区间个数。可能modify_t add del函数有一丢丢不好写! ？! 我们利用前缀异或和。若区间[l,r]满足要求则sum[r]^sum[l-1]=0，即sum[r]=sum[l-1]。所以这个题我们就转化为了区间内有多少对相同的数嘻嘻。需要注意的是每次查询区间[L,R]时我们应变成[L-1,R]。因为sum[r]=sum[l-1]这句话。再者需要注意的是，这个题好像子区间不能只取一堆(假如真的只取1堆只能这堆为0 相当于没取) 。对于时间tt的移动应该放在dexl,dexr移动之后！！再者block=pow(n,2.0/3) sqrt直接T。
emmm还有交换x x+1堆，x+1堆的sum[x+1]是不会变的。modify_t是只需要修改x+1的。这次撤回修改与添加修改都是同一个一样的函数。因为撤销修改也是x与x+1再交换回来。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define en '\n'
#define m(a,b) memset(a,b,sizeof a)
using namespace std;
typedef long long ll;
const int N=1e5+5,M=1e6+5;
int a[N],sum[N],p[N],block;
struct Query{int l,r,id,t;}q[N];
int cmp(Query x,Query y){
    if(x.l/block!=y.l/block) return x.l/block<y.l/block;
    if(x.r/block!=y.r/block) return x.r/block<y.r/block;
    return x.t<y.t;
}
ll ans[N],res;
ll bar[M];//桶
void add(int pos) {res+=bar[sum[pos]]++;}
void del(int pos) {res-=--bar[sum[pos]];}
void modify_t(int i,int t){
    int flag=q[i].l<=p[t]&&p[t]<=q[i].r;
    if(flag) del(p[t]);
    sum[p[t]]^=a[p[t]],swap(a[p[t]],a[p[t]+1]),sum[p[t]]^=a[p[t]];
    if(flag) add(p[t]);
}
int main(){
    int n,m;
    while(~scanf("%d%d",&n,&m)){
        m(bar,0);//block=sqrt(n);
        block=max(10,(int)pow(n,2./3));
        for(int i=1;i<=n;++i) scanf("%d",&a[i]),sum[i]=sum[i-1]^a[i];
        int qcnt=0,kcnt=0;
        while(m--){
            int op,x,l,r;scanf("%d",&op);
            if(op==1) scanf("%d%d",&l,&r),q[++qcnt]=(Query){l-1,r,qcnt,kcnt};//注意是l-1
            else scanf("%d",&x),p[++kcnt]=x;
        }
        sort(q+1,q+qcnt+1,cmp);
        int dexl=1,dexr=0,tt=0;res=0;
        for(int i=1;i<=qcnt;++i){
            while(dexr<q[i].r) add(++dexr);
            while(dexl>q[i].l) add(--dexl);
            while(dexr>q[i].r) del(dexr--);
            while(dexl<q[i].l) del(dexl++);
            while(tt<q[i].t) modify_t(i,++tt);
            while(tt>q[i].t) modify_t(i,tt--);
            ans[q[i].id]=(ll)(q[i].r-q[i].l)*(q[i].r-q[i].l+1)/2-res;
        }
        for(int i=1;i<=qcnt;++i) printf("%lld\n",ans[i]);
    }
}