Wishart分布及Inverse Wishart分布

申明：

        本博客仅作为博主的学习笔记，转载自  数据学习 的博主：小木 ，优快云博主：风吹草地现牛羊的马 以及 百度百科。

原文链接：

•  https://www.datalearner.com/blog/1051508471131357             ​​
•  https://baike.baidu.com/item/%E9%80%86%E5%A8%81%E6%B2%99%E7%89%B9%E5% 88%86%E5%B8%83/22820088?fr=aladdin
• https://blog.youkuaiyun.com/mch2869253130/article/details/107303472

---

---

Wishart分布

引出

为什么要用Wishart分布？

假设从一元正态分布中抽取的n个独立样本，则这些样本的方差应该服从自由度为的分布（具体介绍见如何抽取样本方差的分布）。而Wishart分布是分布在多元上的推广。因此，它可以用来描述多元正态分布样本的协方差矩阵。它在多元正态分布分布的贝叶斯推导中非常重要。

定义

角度一

角度二 

 概率密度函数

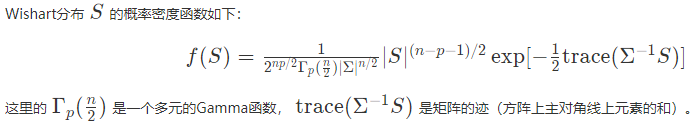
 注意：

        实际上，这个概率密度函数的具体形式很少用到，但其具有很大作用：

• Wishart分布作为 正态分布的协方差矩阵的逆的共轭先验分布，用来描述正态分布的协方差矩阵
• 当一个对称的正定矩阵是扩散张量研究正所感兴趣的随机元素的时候，这个分布也很重要

Wishart分布的命题

Wishart分布的重要作用

Conjugate Bayesian analysis of the Gaussian distribution截图部分

---

---

逆Wishart分布

逆威沙特分布会用作多变量正态分布协方差矩阵的共轭先验分布

概率密度函数

 高斯-逆Wishart分布

Conjugate Bayesian analysis of the Gaussian distribution截图部分