【Gym-101775 L】SOS【思维博弈】

题意：

长度为 $1\ast n$ 的格子，两个人轮流操作，每次往格子上放一个 $S$ 或者 $O$，一旦出现 $SOS$，则为胜。否则为平局。$(1\le n\le 1000)$

---

思路：

博弈题，不能使用 $SG$ 函数，也没有现成的博弈模型可以套用，因此是一个找规律的题目。

我们可以不断对小数据进行模拟。发现 $1～6$ 均为平局，当 $n=7$ 时，先手必胜。

先手可以在中间放一个 $S$ 将区域分成两块，接下来无论后手如何放，先手在另一端端点放一个S，则后手必输。

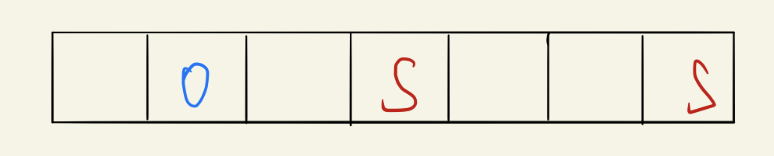
然后可以发现，当 $n\ge 7$ 且 $n$ 为奇数，则先手可以先占住 $7$ 个格子的中间，然后剩下的格子为偶数，如果后手在剩余格子中放置，则先手也在剩余格子中放置，最后后手仍然要回到先手构造的7个格子中，因此先手必胜。

但是 $n\ge 7$ 且 $n$ 为偶数，后手不一定可以构造出一个长度为 $7$ 的区域，因为先手会组织后手。

只有当 $n\ge 16$ 时，无论先手怎么放，后手都拥有一个完整的长度为 $7$ 的区间，因此 $n\ge 16$ 且 $n$ 为奇数，后手必胜。其余情况均为平。

---

总结：

博弈问题，除了固定模型与 $SG$ 函数适用的问题之外，其余博弈问题均为找规律问题，但这类找规律问题往往很难。

其基本思路一般是小数据模拟找到最基本的必胜态，再根据最基本的必胜态往外进行推广。推广的时候要善于进行构造。

在小数据部分，也常常涉及到构造，根据题意构造一些必败态，并且让后手只有进入必败态这一种选择。

观察、构造、小数据模拟大数据推广，堪称找规律博弈的三大法宝。

---

代码：

#include <bits/stdc++.h>
#define __ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define rep(i,a,b) for(int i = a; i <= b; i++)
#define LOG1(x1,x2) cout << x1 << ": " << x2 << endl;
#define LOG2(x1,x2,y1,y2) cout << x1 << ": " << x2 << " , " << y1 << ": " << y2 << endl;
#define LOG3(x1,x2,y1,y2,z1,z2) cout << x1 << ": " << x2 << " , " << y1 << ": " << y2 << " , " << z1 << ": " << z2 << endl;
typedef long long ll;
typedef double db;
const db EPS = 1e-9;
using namespace std;

int main()
{
	int _; scanf("%d",&_);
	rep(Ca,1,_){
		int n; scanf("%d",&n);
		printf("Case #%d: ",Ca);
		if(n < 7) printf("Draw\n");
		else if(n%2) printf("Panda\n");
		else if(n >= 16) printf("Sheep\n");
		else printf("Draw\n");
	}	
	return 0;
}