2019南昌邀请赛网络赛 H. Coloring Game（简单快速幂）

目录

 

【题面】

【题解】

【代码】

---

【题面】

Coloring Game

【题解】

题意：给定一个n，在2*n的网格里，从左上角到右下角有多少种走法。可以横着走也可以斜着走。

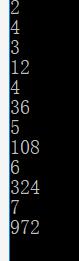
思路：往回走是没意义的，打表发现走法满足公式： ，快速幂即可。

#include <bits/stdc++.h>
using namespace std;
int sum,n;
void dfs(int x,int y)
{
    if(x<1||x>2||y<1||y>n) return;
    if(x==2&&y==n){
        sum++;
        return;
    }
    dfs(x+1,y);
    dfs(x,y+1);
    dfs(x-1,y+1);
    dfs(x+1,y+1);
}
int main()
{
    while(~scanf("%d",&n)){
        sum=0;
        dfs(1,1);
        printf("%d\n",sum);
    }
    return 0;
}

【代码】

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=1e9+7;
ll quick_pow(ll a,ll b)
{
    ll ret=1;
    while(b){
        if(b&1) ret=ret*a%mod;
        a=a*a%mod;
        b=b/2;
    }
    return ret;
}
int main()
{
    ll n; scanf("%lld",&n);
    ll ans;
    if(n==1) ans=1;
    else ans=(4*quick_pow(3,n-2))%mod;
    printf("%lld\n",ans);
    return 0;
}