【ICPC模板】σ因数和函数

最新推荐文章于 2024-06-15 12:05:53 发布

geometry visibility

最新推荐文章于 2024-06-15 12:05:53 发布

阅读量783

点赞数 1

CC 4.0 BY-SA版权

分类专栏： ACM

本文链接：https://blog.youkuaiyun.com/qq_39286680/article/details/87090864

ACM 专栏收录该内容

26 篇文章

订阅专栏

本文详细介绍了数学中因数和函数σ(n)的概念，该函数表示从1到n（包含）的所有n的因数之和。通过讨论其积性和求值公式，文章提供了一个高效的算法实现，利用欧拉线性筛素数函数和快速幂函数来计算σ(n)，并展示了完整的C++代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

含义：σ(n)表示从1到n（包含）的所有n 的因数之和。

积性：如果gcd(n, m) = 1，有σ(nm) = σ(n) * σ(m)

求值公式：

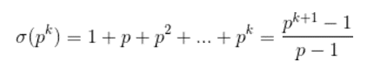
特别地：

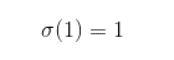
代码：

#include <iostream>

using namespace std;

const int LIM = 1e7;
int prime[LIM];
int pos;
bool notPrime[LIM];

void Euler() {
    for (int i = 2; i < LIM; i++) {
        if (!notPrime[i]) prime[pos++] = i;
        for (int j = 0; j < pos; j++) {
            int tmp = prime[j] * i;
            if (tmp >= LIM || tmp < 0) break;
            notPrime[tmp] = true;
        }
    }
}

int fastPow(int b, int p) {
    int ret = 1;
    while (p) {
        if (p & 1) ret *= b;
        b *= b;
        p >>= 1;
    }
    return ret;
}

// sigma因数和函数
int sigma(int n) {
    int ret = 1;
    for (int i = 0; i < pos && n > 1; i++) {
        int cnt = 0;
        while (!(n % prime[i])) n /= prime[i], cnt++;
        if (cnt) ret *= (fastPow(prime[i], cnt + 1) - 1) / (prime[i] - 1);
    }
    return ret;
}

int main(void) {
    Euler();
    int t, n;
    scanf("%d", &t);
    while (t--) {
        scanf("%d", &n);
        printf("%d\n", sigma(n) - n);
    }
    return 0;
}

依赖：

-欧拉线性筛素数函数

-快速幂（逐次平方法）函数