sigmoid函数

$$\sigma (x)=\frac{1}{1+e^{-x}}$$

sigmoid函数好处

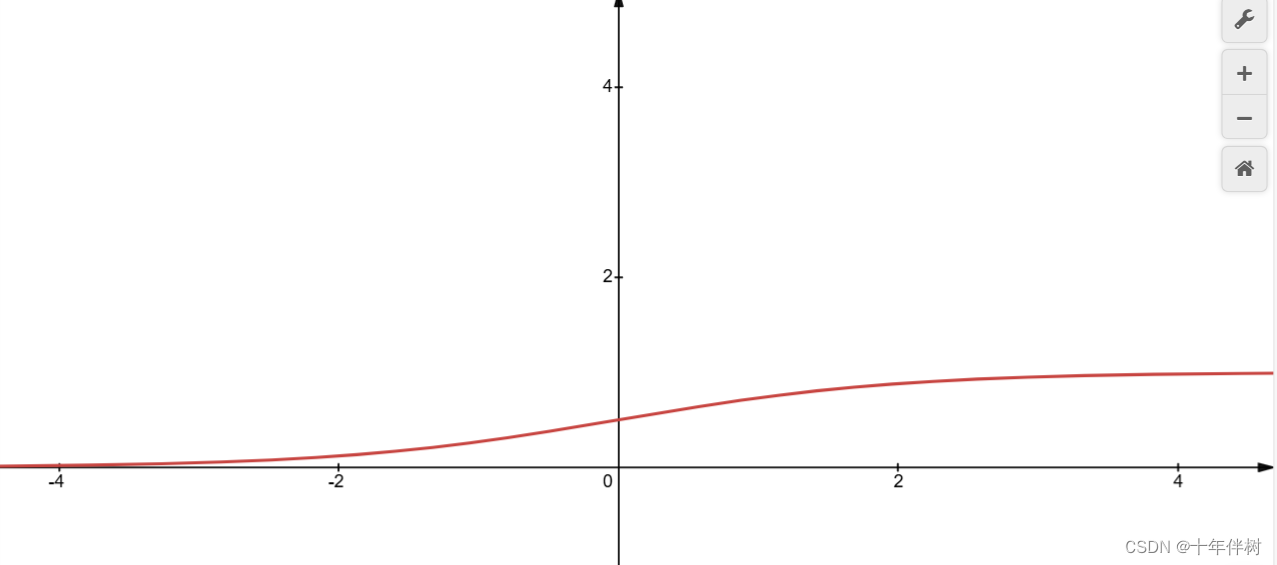
1.$\sigma (x)$的域值是[0,1] ，在(-∞, +∞)单调递增，很符合概率分布函数的特点
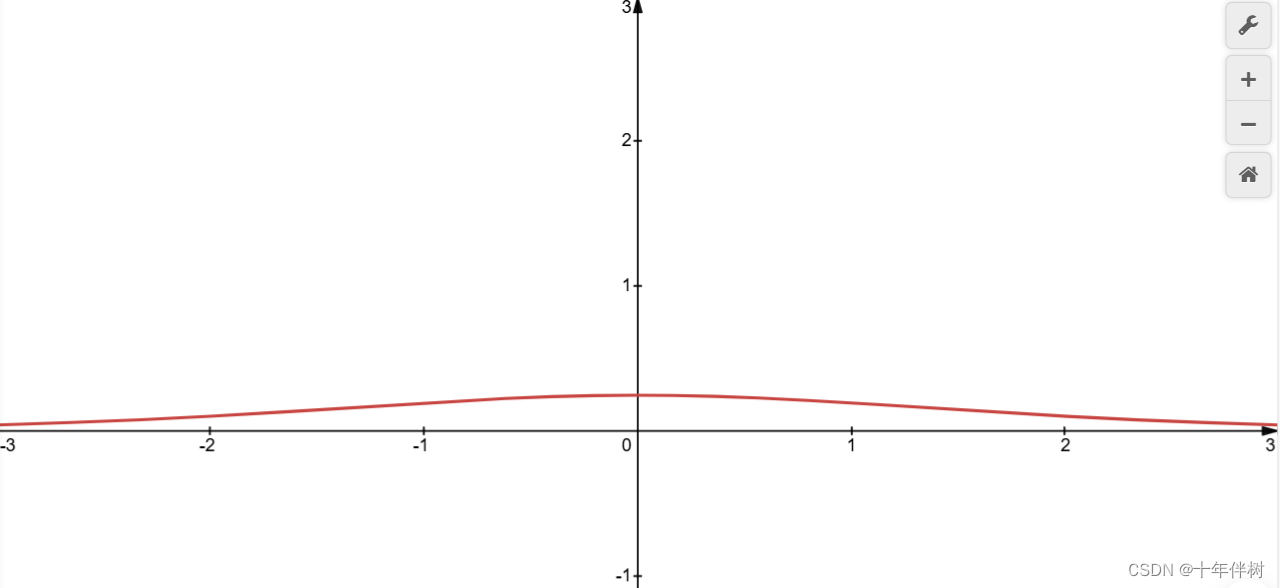
2.以$\sigma (x)$为分布函数的概率密度函数在远离零点的位置概率趋近于0，这样比较符合现实生活中的一些规律，即在一定基准线上下浮动，大部分在基准线
3.不同于高斯分布，$\sigma (x)$比较容易求导，即$\sigma (x{)}^{{}^{\prime }}=\sigma (x)(1-\sigma (x))$对计算机比较友好
4.$\sigma (x)$同样也可以伸缩变换和平移，如
$$\sigma (x)=\frac{u}{1+e^{-x}}$$
u是上限阈值

Fig. 1.1 sigmoid函数-概率分布函数

Fig. 1.2 sigmoid函数的导数-概率密度函数