目录
一元线性同余方程(Linear Congruence Equation)
中国剩余定理 (Chinese Remander Theorem, CRT)
费马大定理 (Le dernier théorème de Fermat)
费马小定理 (Fermat's little theorem)
Miller-Rabin Primality Test(米勒-罗宾随机素性测试)
Number Theory(数论)
扩展欧几里得
递归实现
代码较简短
// ret value which is gcd(a, b)
// x is coefficient of a
// y is coefficient of b
void ex_gcd(LL a, LL b, LL &r, LL &x, LL &y) {
if (!b) {r = a, x = 1, y = 0;}
else {
ex_gcd(b, a % b, r, y, x);
y -= x * (a / b);
}
}
递推实现
使用这个函数可以求解形如ax + by = gcd(a, b)方程的x和y整数解。
注意:这个gcd函数假设了b不为0,b如果为0会出现除以0的错误。另外,a如果为0,结果也将不正确。
/* ax + by = gcd(a, b) */
/* x = xpp - q * xp */
/* y = ypp - q * yp */
/* xpp 表示 x pre pre, 即x(n - 2), 其余同理 */
LL ex_gcd(LL a, LL b, LL &x, LL &y) {
LL xp, xpp, yp, ypp;
LL r, q;
q = a / b, r = a % b;
xpp = x = 0, ypp = y = 1;
if (!r) return b;
xp = x = 1, yp = y = -q;
while (true) {
a = b, b = r;
q = a / b, r = a % b;
if (!r) return b;
x = xpp - xp * q;
y = ypp - yp * q;
xpp = xp, ypp = yp;
xp = x, yp = y;
}
}
得到(0, mod]之间最小同余整数
// 介于(0, mod]的最小模mod同余整数
template <class T>
T toPositive(T x, T mod) {
x = ((x % mod) + mod) % mod;
return x ? x : mod;
}
得到[-mod, 0)之间最大同余整数
// 介于[-mod, 0)的最大模mod同余整数
template <class T>
T toNegative(T x, T mod) {
x = ((x % mod) - mod) % mod;
return x ? x : -mod;
}
一元线性同余方程(Linear Congruence Equation)
![]()
#include <iostream>
using namespace std;
typedef long long LL;
/* ax + by = gcd(a, b) */
/* x = xpp - q * xp */
/* y = ypp - q * yp */
/* xpp 表示 x pre pre, 即x(n - 2), 其余同理 */
template <class T>
T ex_gcd(T a, T b, T &x, T &y) {
T xpp, xp;
T ypp, yp;
T r = a % b, q = a / b;
if (!r) {
x = 0, y = 1;
return b;
}
xpp = 0, ypp = 1;
x = xp = 1, y = yp = -q;
while (true) {
a = b;
b = r;
q = a / b, r = a % b;
if (!r) return b;
x = xpp - q * xp, y = ypp - q * yp;
xpp = xp, ypp = yp;
xp = x, yp = y;
}
}
// 介于(0, mod]的最小模mod同余整数
template <class T>
T toPositive(T x, T mod) {
x = ((x % mod) + mod) % mod;
return x ? x : mod;
}
// 介于[-mod, 0)的最大模mod同余整数
template <class T>
T toNegative(T x, T mod) {
x = ((x % mod) - mod) % mod;
return x ? x : -mod;
}
// EVERY表示任意值都是解, NIL表示无解
enum {EVERY = -2, NIL = -1};
// 求解形如ax = b (mod c)的Linear Congruence Equaltion(线性同余方程)
// 使用ex_gcd求解ax + cy = b
LL linearCongruence(LL a, LL b, LL c) {
a = toPositive(a, c) % c;
b = toPositive(b, c) % c;
// if (!a && !b) return EVERY;
if ((!a && b) || !c) return NIL;
// else if (a && !b) return 0;
// 当a小于0时, 将符号交给x, 此时xnf为真
// 表示x Negative Flag
bool xnf = false, ynf = false;
if (a < 0) xnf = true, a = -a;
if (c < 0) ynf = true, c = -c;
b = toPositive(b, c);
// g = gcd(a, c)
LL x, y, g;
g = ex_gcd(a, c, x, y);
if (b % g) return NIL;
if (xnf) {
x = toNegative(x, c / g);
x = -x;
} else {
x = toPositive(x, c / g);
}
// b此时一定能被g整除
// 括号在一定程度上防止因为极端数据导致溢出
// 对c取模得到[0, c / g - 1]之间解,即最小正数解
return x * (b / g) % (c / g);
}
依赖:
-扩展欧几里得
-得到(0, mod]之间最小同余整数
-得到[-mod, 0)之间最大同余整数
多元一次不定方程(丢番图方程)求解
核心:
首先移项,左边仅剩下ax + by,使用扩展欧几里得求解x和y,其右侧值应当满足能够整除gcd(a, b),接着用扩展gcd求解gcd(a, b)和c的参数,c的参数z将作为中间过程的答案,而gcd(a, b)的倍数将用来给前面求过的所有结果翻倍,以此类推。
方程有解当且仅当右侧常数c能够整除gcd(a, b, c, d……)。
代码:
#include <iostream>
#include <vector>
using namespace std;
typedef long long LL;
int ex_gcd(int a, int b, int &x, int &y) {
int xp, xpp, yp, ypp;
int r, q;
q = a / b, r = a % b;
xpp = x = 0, ypp = y = 1;
if (!r) return b;
xp = x = 1, yp = y = -q;
while (true) {
a = b, b = r;
q = a / b, r = a % b;
if (!r) return b;
x = xpp - xp * q;
y = ypp - yp * q;
xpp = xp, ypp = yp;
xp = x, yp = y;
}
}
// 返回false表示无解
// 当所有元素的gcd无法整除常数c时,方程无整数解
const int LIM = 1e6 + 10;
int multi[LIM], ans[LIM], coefficient[LIM];
bool indeterEqualtion(int *coefficient, int *ans, int len, int c) {
if (len == 1) {
if (c % coefficient[0]) return false;
ans[0] = c / coefficient[0];
return true;
}
// init
int g = ex_gcd(coefficient[0], coefficient[1], ans[0], ans[1]);
for (int i = 2; i < len; i++)
g = ex_gcd(g, coefficient[i], multi[i - 1], ans[i]);
if (c % g) return false;
int sufmul = 1;
for (int i = len - 2; i; i--)
sufmul *= multi[i], ans[i] *= sufmul;
ans[0] *= sufmul;
return true;
}
int main(void) {
ios::sync_with_stdio(false);
coefficient[0] = 155;
coefficient[1] = 341;
coefficient[2] = 385;
indeterEqualtion(coefficient, ans, 3, 1);
for (int i = 0; i < 3; i++) {
if (i) cout << ' ';
cout << ans[i];
}
cout << endl;
return 0;
}
中国剩余定理 (Chinese Remander Theorem, CRT)
中国剩余定理描述的是一种求解一元线性方程同余组的方法,形如下图:
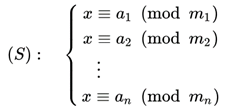
使用这一方法有一个前提是:对于任意两个模数m[i]和m[j](注:此处[]中的内容表示下标),应有gcd(m[i], m[j]) = 1,即二者互素。
中国剩余定理的核心是“构造”,它给出了一种构造此类方程组解的方法。
令M表示全体模数m[i]的乘积,用M[i]表示全体模数的乘积M除以m[i]的值(即除了第i个模数m[i]之外所有模数的乘积)。接着令t[i]表示M[i]对m[i]取模的逆元,此时有t[i] * M[i]模除m[i]后余数为1.
接着,使用a[i]乘上t[i] * M[i],得到的结果(即a[i] * t[i] * M[i])具有这样的性质:如果将它对m[i]取余,则因为t[i] * M[i]对m[i]取余是1,因此a[i] * t[i] * M[i]对m[i]取余得到a[i];如果将它对排除m[i]之外任意一个模数(后面用m[j]表示)取模,因为M[i]表示排除m[i]之后所有模数的乘积,可知m[j]是M[i]的因数,那么m[j]就可以整除a[i]*t[i]*M[i],余数为0.
根据这样的性质,将所有的a[i] * t[i] * M[i]加和就得到这个方程组的一个解,实际上它加减任意个M都是这个方程组的解。
解的通式符号表示如下:
![]()
扩展中国剩余定理 (扩展CRT)
扩展CRT问题与一般CRT问题相同,可以理解为是CRT问题的一种更加通用的解法。
相较于一般的中国剩余定理,它可以用来解决模数之间不互质的情况,同时仍然可以解决互质的情况。需要使用扩展欧几里得方法。
整体方法是合并,将多个同余式合并,直到最后只剩下一个,进行求解。
对于两个同余式:![]()
![]()
写成等式的形式,并进行联立:
![]()
移项得到①式:
![]()
当且仅当:
![]()
成立时方程有整数解k1与k2,这将作为判断不定方程组是否有解的条件。
在有解的情况下,可以将①式整理成:
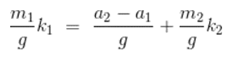
其中g = gcd(m1, m2)
这等价于:








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 1740
1740

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








