手撕算法准备

稳定的穷

已于 2022-09-18 09:16:04 修改

阅读量968

点赞数

分类专栏：面试应对笔记文章标签： java

于 2022-04-01 13:58:11 首次发布

本文链接：https://blog.youkuaiyun.com/qq_39227541/article/details/123896174

版权

面试应对笔记专栏收录该内容

18 篇文章

订阅专栏

排序算法（复杂度）

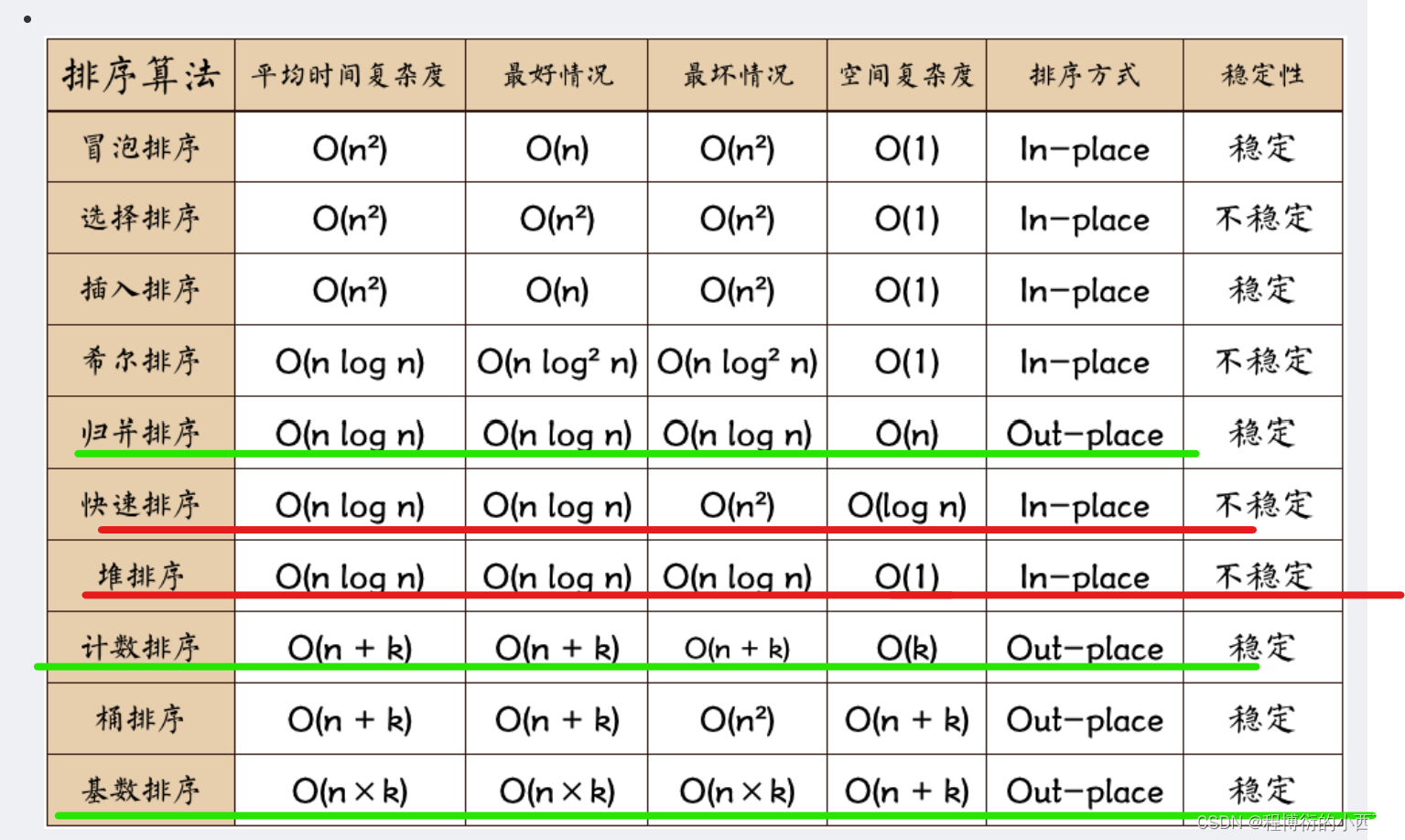
在这里插入图片描述

在这里插入图片描述
鉴别的解释

在这里插入图片描述

冒泡&&选择&&插入排序（两层for循环）

    /**
     * 冒泡排序
     * @param nums
     */
    public static void bubbleSort(int[] nums){
        int len=nums.length;
//        每一轮将最大的数逐渐移动至未排序数组的最后一个位置
//        冒泡排序的趟数
        for(int i=1;i<len;i++){
            for(int j=0;j<len-i;j++){
                if(nums[j]>nums[j+1]){
                    swap(nums,j,j+1);
                }
            }
        }
    }

    /**
     * 选择排序：进行多趟的排序，每次从未排序数组中寻找最小的数，放在开头的位置
     * @param nums
     */
    public static void selectSort(int[] nums){
        int len=nums.length;

        for(int i=0;i<len-1;i++){
            int minIndex=i;
            for(int j=i+1;j<len;j++){
                if(nums[j]<nums[minIndex]) {
                    minIndex = j;
                }
            }
            swap(nums,i,minIndex);
        }

    }


    /**
     * 插入排序：分为已排序数组和未排序数组，总是拿未排序数组的第一个元素与已排序比较插入
     * @param arr
     */
    public static void insertSort(int[] arr){
        int insert;//待插入元素的值
        int index=0;//待插入元素的当前序号---本质：次序号之前的数均是排好序的数

        //默认的第一个数已经是有序数组的一员
        for (int i = 1; i < arr.length; i++) {
            insert=arr[i];
            index=i;//这个序号之前的数已经排好序的
            //可能出现前面的数全部比要插入的数大，也就是前面的数基本所有都往后移了个位置
            boolean flag=false;
            for (int j = index-1; j >=0; j--) {
                if(arr[j]>insert){
                    arr[j+1]=arr[j];//此时需要将当前的元素往后移动
                }else{//说明本元素后面的那个空位置就是我的位置(12 45  "3"678 )
                    flag=true;
                    arr[j+1]=insert;
                    break;//一旦找到了位置就直接退出，防止数据被覆盖
                }
            }
            if(!flag){
                arr[0]=insert;//出现前面的数全部比要插入的数大，插入的数放在了头部，之前所有的数都后移了一个位置
            }
        }
    }



    public static void swap(int[] nums,int i,int j){
        int temp=nums[i];
        nums[i]=nums[j];
        nums[j]=temp;
    }

堆排序(大顶堆–用于升序排列)—数组转化为顺序存储二叉树

在这里插入图片描述

==step1:==调整堆的方法（用于将一个非叶子节点的子树的最大数移动至堆顶）
==step2:==构建一个初始化的堆（规矩建堆，方便后续，自下而上建堆，寻找第一个最大的数）
==step3：==循环调整大顶堆，将堆顶元素与未排序的最后一个位置交换，相当于每次找到一个次大值。
在这里插入图片描述

public class BigHeapSort {
    public static void main(String[] args) {
        int[] nums={6,1,1,2,7,9,10,4,5,8};
        heapSort(nums,nums.length);
        for (int num : nums) {
            System.out.println(num);
        }
    }


    public static void  heapSort(int[] nums,int len){
        //初始化构建大顶堆（自下而上，最终结束最顶端的是数组的最大的数）
        //最后一个非叶子结点对应的序号是nums.length/2-1
        for(int i=len/2-1;i>=0;i--){
            adjustHeap(nums,i,len);
        }

        //每次寻找未排序的最大数，移动至堆顶
        for(int i=len-1;i>=1;i--){
            swap(nums,0,i);//将0位置的未排序最大数，放到未排序序号的最后一个位置
            adjustHeap(nums,0,i);//确保0位置的数是未排序的最大数
        }
    }


    /**
     *
     * @param nums:需要顺序结构化的二叉树
     * @param start：开始调整的非叶子结点的序号
     * @param len：实际就是定位未排序的最后一个位置的序号
     */
    public static void adjustHeap(int[] nums,int start,int len){
        int bigIndex=start;
        //注意一个序号为k的节点的左子节点的序号：2*k+1，右子节点的序号2*k+2
        for(int k=bigIndex*2+1;k<len;k=k*2+1){
            //取左右子节点较大的那个数
            if(k+1<len && nums[k+1]>nums[k]){
                k++;
            }
            if(nums[bigIndex]<nums[k]){
                swap(nums,bigIndex,k);
                bigIndex=k;//相当于转移到了右子节点的树的后需调整过程
            }
//            else{
//                break;//实际上可以直接结束,原因初始化堆的时候是自下而上构造的，保证了一定的大小顺序性
//            }
        }
        
    }

    public static void swap(int[] nums,int i,int j){
        int temp=nums[i];
        nums[i]=nums[j];
        nums[j]=temp;
    }
}

快速排序

在这里插入图片描述
==step1:==寻找要的随机的base的序号，并将它放到最start的位置
==step2:==将小于等于base的数放在左边，大于等于base的数放在最右边（最后双指针指向的同一个数与base的start位置交换，就保证了这个相等位置的数左边都是小于等于它的数，右边都是大于等于它的数）—注意一些遍历顺序的细节
==step3:==左右两段内的数是没有顺序的，所以需要继续递归的排序子片段的数组

public class QuickSort {
    public static void main(String[] args) {
        int[] nums={6,1,1,2,7,9,10,4,5,8};
        quickSort(nums,0,nums.length-1);
        for (int num : nums) {
            System.out.println(num);
        }

    }

    public static void quickSort(int[] nums,int start,int end){
        if(start>=end){
            return;//说明已经不用排了
        }

        int indexRandom=randomIndex(nums,start,end);
        //将要作为base的数放在最左边的起始位置
        swap(nums,start,indexRandom);
        int base=start;
        int i=base;
        int j=end;
        while(i<j){
            //因为退出整个循环时，交换的base和i,所以确保最终i指向的数小于base（必须把j的循环写在前面）
            //确保退出循环时的j指向小于base的数，这样退出整个循环的时候i,j指向的同一个数也是小于base的数
            while(i<j && nums[j]>=nums[base]){
                j--;
            }
            while(i<j && nums[i]<=nums[base]){
                i++;
            }
            swap(nums,i,j);
        }

        swap(nums,i,base);//此时i==j
        quickSort(nums,start,i-1);
        quickSort(nums,i+1,end);

    }

    //寻找随机的base的序号
    public static int randomIndex(int[] nums,int start,int end){
        return new Random().nextInt(end-start+1)+start;//生成一个start-end之间的随机数
    }

    public static void swap(int[] nums,int start,int end){
        int temp=nums[start];
        nums[start]=nums[end];
        nums[end]=temp;
    }
}

归并排序（没在原数组进行排序）


public class MergerSort {
    public static void main(String[] args) {
        int[] nums={6,1,1,2,7,9,10,4,5,8};
        int[] res=mergeSort(nums);

        for (int num : res) {
            System.out.println(num);
        }
    }

//拆分数组并进行合并排序的过程
    public static int[] mergeSort(int[] arr){
        if(arr.length<2){
            return arr;//说明数组只有一个元素，直接返回
        }
        //将数组不断拆分，
        int mid=arr.length/2;
        int[] left= mergeSort(Arrays.copyOfRange(arr,0,mid));//不包括这个mid
        int[] right=mergeSort(Arrays.copyOfRange(arr,mid,arr.length));
        
        //然后最后自下而上进行往上合并
        return merge(left,right);

    }

//将两个有序数组进行合并
    public static int[] merge(int[] left,int[] right){
        int[] resMerge=new int[left.length+right.length];
        int leftlen=left.length;
        int rightlen=right.length;
        int i=0,j=0;
        for(int n=0;n<resMerge.length;n++){
            if(i>=leftlen){
                resMerge[n]=right[j];
                j++;
            }else if(j>=rightlen){
                resMerge[n]=left[i];
                i++;
            }else if(left[i]<right[j]){
                resMerge[n]=left[i];
                i++;
            }else{
                resMerge[n]=right[j];
                j++;
            }
        }
        return resMerge;
    }
}

桶排序

计数排序（桶的个数==元素取值范围）–空间复杂度大

本质：统计每个元素的值出现的次数，统计完后再依次输出（类似构造了一个hashmap数组，键为数值，值为出现的次数，之后按序输出----序号/序号加上偏移量）
在这里插入图片描述

、public class CountSort {
    public static void main(String[] args) {
        int[] nums={6,1,1,2,2,7,9,10,13,5,8,16};
        countSort(nums);
        for (int num : nums) {
            System.out.println(num);
        }
    }

    public static void countSort(int[] nums){
        int max=nums[0];
        int min=nums[0];
        for(int i=0;i<nums.length;i++){
            max=Math.max(max,nums[i]);
            min=Math.min(min,nums[i]);
        }

        int[] bucket=new int[max-min+1];
        for(int i=0;i<nums.length;i++){
            bucket[nums[i]-min]++;
        }

        int index=0;//待排序数组的填入序号
        int start=0;//桶的序号
        while(index<nums.length){
            while(bucket[start]!=0){
                nums[index]=start+min;
                bucket[start]--;
                index++;
            }
            start++;//对桶进行递增
        }
    }
}

基数排序（桶的个数==最大值的位数）–空间复杂度小，较复杂

需要进行多轮的按照基数的位置排序，每次从低到高的轮数进行基数排序
构造10个桶：分别对应数值0-9对应装的数据（注意：初始化每个桶的大小需要为原始数组的大小，比较浪费空间）+需要构造每个桶的放入数据个数的指针，实时更新
需要进行排序的整体轮数：数组中最大的数的位数

public class BaseSort {
    public static void main(String[] args) {
        int[] nums = {6, 1, 1, 2, 2, 7, 9, 10, 13, 5, 8, 16};
        baseSort(nums);
        for (int num : nums) {
            System.out.println(num);
        }

    }


    public static void baseSort(int[] nums){
        int max=nums[0];
        int len=nums.length;
        //寻找 数组中的最大值
        for (int i = 0; i < len; i++) {
            max=Math.max(max,nums[i]);
        }

        int bucketCon=(max+"").length();//最大数的位数
        int[][] bucket=new int[10][len];//需要预留足够大的空间
        int[] bucketPoint=new int[10];//实时更新每个桶的数的个数

        //一共需要bucketCount轮的排序（n=1,10,..便于计算每一位的数值）
        for(int k=0,n=1;k<bucketCon;k++,n=n*10){
            //按序入桶
            for(int i=0;i<len;i++){
                bucket[(nums[i]/n)%10][bucketPoint[(nums[i]/n)%10]]=nums[i];
                bucketPoint[(nums[i]/n)%10]++;
            }

            //按序出桶(按照各个位的0-9按序回到原来的数组位置中)
            int index=0;
            for(int i=0;i<10;i++){
                for(int j=0;j<bucketPoint[i];j++){
                    nums[index]=bucket[i][j];
                    index++;
                }
                bucketPoint[i]=0;//清零，下轮复用
            }
        }

    }
}

手写设计模式

工厂模式

public class OfferFactory {
    public Offer getOffer(String size){
        size=size.toLowerCase();
        switch (size){
            case "big":
                return new BigOffer();
            case "middle":
                return new MiddleOffer();
            default:
                return new SmallOffer();

        }

    }
}

public interface Offer {
    void getOffer();
}

public class BigOffer implements Offer{
    @Override
    public void getOffer() {
        System.out.println("你的大厂offer");
    }
}

public class MiddleOffer implements Offer{
    @Override
    public void getOffer() {
        System.out.println("你的中厂offer");
    }
}

public class SmallOffer implements Offer{
    @Override
    public void getOffer() {
        System.out.println("你的小厂offer");
    }
}

public class TestFactory {
    public static void main(String[] args) {
//        注意工厂模式一般是创建你需要的对象，但是抽象工厂会进一步创建你需要的工厂之后，在创建你需要的对象
        OfferFactory offerFactory = new OfferFactory();
        Offer offer = offerFactory.getOffer("Big");
        offer.getOffer();
    }
}

在这里插入图片描述

观察者模式

//这个是被观察的像
public class Subject {

//    肯定有一个绑定的观察者的集合，确保改变状态的时候可以通知到所有放入观察者
    private ArrayList<Observer> observers=new ArrayList<>();
    private int state;

    public int getState(){
        return state;
    }

//    注意改变状态需要通知所有放入观察者进行更新
    public void setState(int val){
        this.state=val;
        adviceObserver();
    }

    public void bindObserver(Observer observer){
        observers.add(observer);
    }

    public void adviceObserver(){
        for(Observer observer:observers){
            observer.update();
        }
    }

}

public abstract class Observer {
    protected Subject subject;
    abstract void update();
    abstract void bindSubject(Subject sub);
}


public class ExamObserver extends Observer{

    @Override
    public void update() {
        System.out.println(subject.getState()+"笔试阶段了");

    }

    @Override
    public void bindSubject(Subject sub) {
        this.subject=sub;
        subject.bindObserver(this);
    }
}


public class InterviewObserver extends Observer{
    @Override
    void update() {
        System.out.println(subject.getState()+"面试了");

    }

    @Override
    void bindSubject(Subject sub) {
        this.subject=sub;
        subject.bindObserver(this);
    }
}


public class OfferObserver extends Observer{
    @Override
    void update() {
        System.out.println(subject.getState()+"offer到了");
    }

    @Override
    void bindSubject(Subject sub) {
        this.subject=sub;
        subject.bindObserver(this);
    }
}

public class TestObserver {
    public static void main(String[] args) {
        Subject subject=new Subject();



        ExamObserver examObserver = new ExamObserver();
        examObserver.bindSubject(subject);

        subject.setState(10);
        InterviewObserver interviewObserver = new InterviewObserver();
        interviewObserver.bindSubject(subject);

        subject.setState(20);
        OfferObserver offerObserver = new OfferObserver();
        offerObserver.bindSubject(subject);

        subject.setState(30);



    }
}

在这里插入图片描述

多线程

别的一些问题，在高并发的面筋中

三个线程循环打印

Synchronized的版本

public class Synchronized3 {
    public static void main(String[] args) {
        PrintABC printABC = new PrintABC();
        int num=20;
        new Thread(new Runnable() {
            @Override
            public void run() {
                for (int i = 0; i <num ; i++) {
                    printABC.printA();
                }

            }
        }).start();


        new Thread(new Runnable() {
            @Override
            public void run() {
                for (int i = 0; i <num ; i++) {
                    printABC.printB();
                }

            }
        }).start();

        new Thread(new Runnable() {
            @Override
            public void run() {
                for (int i = 0; i <num ; i++) {
                    printABC.printC();
                }
            }
        }).start();


    }
}



//使用同一个实例变量作为锁住的公共对象
class PrintABC{
//    注意：相当于这个num的变量永远只会在synchronized的包裹内进行变换
    int num=1;

    public synchronized void printA(){
    //说明只有在num=1的时候才能实现打印的操作
        while(num!=1){
            try {
                this.wait();
            } catch (InterruptedException e) {
                e.printStackTrace();
            }
        }
        num=2;
        System.out.println("A");
        this.notifyAll();
    }


    public synchronized void printB(){
            while(num!=2){
                try {
                    this.wait();
                } catch (InterruptedException e) {
                    e.printStackTrace();
                }
            }
            num=3;
            System.out.println("B");
            this.notifyAll();
    }

    public synchronized void printC(){
        while(num!=3){
            try {
                this.wait();
            } catch (InterruptedException e) {
                e.printStackTrace();
            }
        }
        num=1;
        System.out.println("C");
        this.notifyAll();
    }
}

ReentranLock版本

public class ReentranLock3 {
    public static void main(String[] args) {
        PrintABC1 printABC1 = new PrintABC1();
        int num=20;
        new Thread(new Runnable() {
            @Override
            public void run() {
                for (int i = 0; i < num; i++) {
                    printABC1.printA();
                }
            }
        }).start();

        new Thread(new Runnable() {
            @Override
            public void run() {
                for (int i = 0; i < num; i++) {
                    printABC1.printB();
                }
            }
        }).start();

        new Thread(new Runnable() {
            @Override
            public void run() {
                for (int i = 0; i < num; i++) {
                    printABC1.printC();
                }
            }
        }).start();

    }
}

//使用同一个实例变量作为锁住的公共对象
class PrintABC1{
    //    注意：相当于这个num=1的变量永远只会在synchronized的包裹内进行变换
    int num=1;
    ReentrantLock lock=new ReentrantLock();
    Condition con1=lock.newCondition();
    Condition con2=lock.newCondition();
    Condition con3=lock.newCondition();


    public void printA(){
        lock.lock();
        try{
         //说明只有在num=1的时候才能实现打印的操作
            if(num!=1){
                con1.await();
            }
            System.out.println("A");
            System.out.println("A");
            System.out.println("A");
            num=2;
            con2.signal();

        }catch(Exception e){

        }finally {
            lock.unlock();
        }
    }

    public void printB(){
        lock.lock();
        try{
            if(num!=2){
                con2.await();
            }
            System.out.println("B");
            System.out.println("B");
            num=3;
            con3.signal();

        }catch(Exception e){

        }finally {
            lock.unlock();
        }
    }

    public void printC(){
        lock.lock();
        try{
            if(num!=3){
                con3.await();
            }
            System.out.println("C");
            num=1;
            con1.signal();

        }catch(Exception e){

        }finally {
            lock.unlock();
        }
    }
    
}

Semaphore版本（保证永远只有一个1）

public class Semaphore3 {
    public static void main(String[] args) {
        PrintABC2 printABC2 = new PrintABC2();
        int num=20;

        new Thread(()-> {
                for (int i = 0; i < num; i++) {
                    printABC2.printA();
                }
        }).start();


        new Thread(() ->{
                for (int i = 0; i < num; i++) {
                    printABC2.printB();
                }
        }).start();

        new Thread(()->{
                for (int i = 0; i < num; i++) {
                    printABC2.printC();
                }
        }).start();

    }
}


class PrintABC2{
//    注意：在0的时候会阻塞住，在1的时候可以获取锁（三个中永远的保证只有一个为1）
    Semaphore SA=new Semaphore(1);
    Semaphore SB=new Semaphore(0);
    Semaphore SC=new Semaphore(0);

    public void printA(){
        try {
            SA.acquire();
            System.out.println("A");
            SB.release();
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
    }


    public void printB(){
        try {
            SB.acquire();
            System.out.println("B");
            SC.release();
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
    }

    public void printC(){
        try {
            SC.acquire();
            System.out.println("C");
            SA.release();
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
    }

}

二叉树（看笔记）

树的笔记

二叉排序/搜索树（前序遍历的关系）

在这里插入图片描述
力扣题：判断一棵树是否是二叉搜索树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        //初始化时的上下界就是正负无穷(为啥需要Long的范围：因为会有一个Integer.Max_value的单独节点，如果使用Integer的最大最小范围：就会出现等于的情况)
        return isNodeV(root,Long.MIN_VALUE,Long.MAX_VALUE);
    }


     //注意左子树的所有节点小于本节点，右子树的所有节点大于本节点(保证本节点在符合的区间内)
     public boolean isNodeV(TreeNode cur,long lower,long upper){
         if(cur==null){
             return true;
         }

         if(cur.val<=lower || cur.val>=upper){
             return false;
         }

        //左孩子的值小于本节点的值，所以上界为本届点的值；右孩子的值大于本节点的值，所以当前的下界改为本届点的值
         return isNodeV(cur.left,lower,cur.val) && isNodeV(cur.right,cur.val,upper);

     }
}

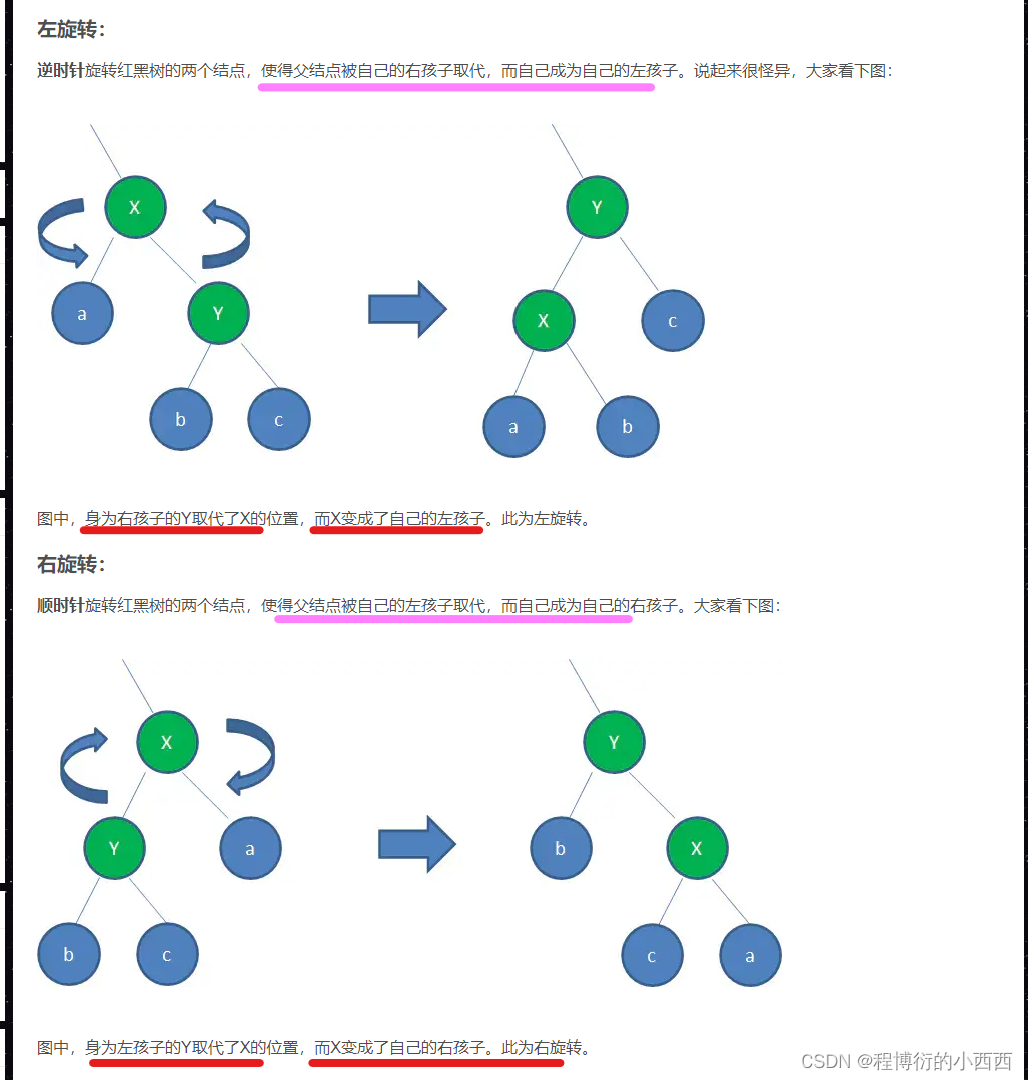
平衡树二叉树（左旋与右旋）

在这里插入图片描述

注意：双旋转AVL书，针对异常的左子树先进行左旋转，之后对整棵树进行右旋转（左旋转与右旋转的步骤还是原来相同！！！）

左旋转思想（右子树太高）

创建一个新的节点值等于当前根节点的值，将新节点的右子树设置为根节点的右子树的左子树&&新节点的左子树设置为根节点的左子树，将原本根节点的左子树的左子树设置为当前的新节点。（显然如果左旋转之后还是不满足，需要继续左旋转）
在这里插入图片描述

右旋转思想（左子树太高）

创建一个新的节点，其值等于当前根节点的值，新节点的左子树等于根节点的左子树的右子树&&新节点的右子树等于根节点的右子树，将原根节点的左子树的右子树指向新的节点

在这里插入图片描述

力扣题：判断一棵树是否是平衡二叉树AVL树
在这里插入图片描述

class Solution {
    public boolean isBalanced(TreeNode root) {
        //当且仅当树的高度大于等于0才是合法的
        return HeightAndBalance(root)>=0;
    }


    //巧妙的利用后序遍历来”高度+平衡“合二为一
    //太妙了：height=-1说明不平衡（子树不平衡的连坐父母），height>0说明高度合法
    public int HeightAndBalance(TreeNode cur){
        if(cur==null){
            return 0;//这个合法
        }

       //注意计算完了放在常量中进行判断，防止多次的计算
        int left_height=HeightAndBalance(cur.left);
        int right_height=HeightAndBalance(cur.right);

        //左右子树本身不平衡 or 本棵树不是平衡的
        if(left_height<0 || right_height<0 || 
           Math.abs(left_height-right_height)>1){
               return -1;
        }else{
            return Math.max(left_height,right_height)+1;
        }
    }
}

class Solution {


    //根据高度判断是否是平衡二叉树
    public boolean isBalanced(TreeNode root) {
            if(root==null){
                return true;
            }
            boolean cur_sit=Math.abs(len_tree(root.left)-len_tree(root.right))<=1?true:false;
            return cur_sit && isBalanced(root.left) && isBalanced(root.right); 

    }

    //计算以cur节点为根节点的每颗树的深度
    public int len_tree(TreeNode cur){
        if(cur==null){
            return 0;
        }
        return Math.max(len_tree(cur.right),len_tree(cur.left))+1;
    }
}

红黑树

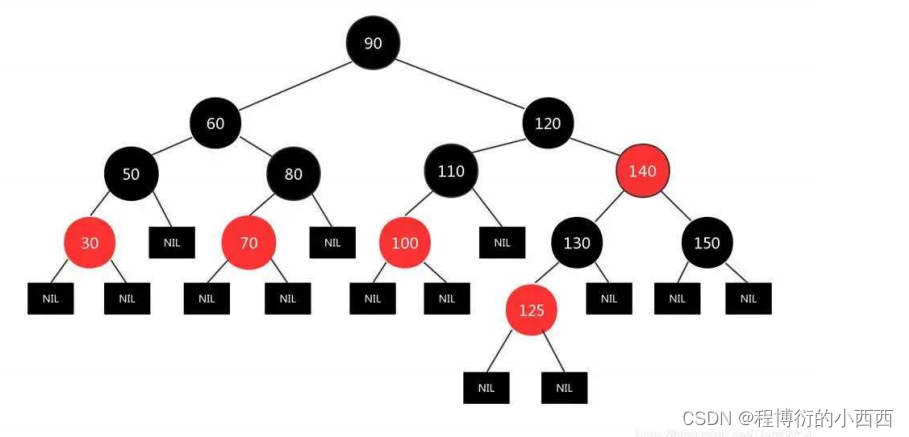
在这里插入图片描述

在这里插入图片描述

确保一个红色节点的两个子节点是黑色的节点，显然x节点不满足，所以直接变为黑色的节点

前缀树

在这里插入图片描述
抽象：关键是成员变量的构造----孩子们（可以是数组–针对字母的情况，可以是hashmap构成的）

class Trie {

    //成员变量（本层孩子+末节点的标志）
    private Trie[] children;
    private boolean isEnd;

    public Trie() {
        children=new Trie[26];
        isEnd=false;
    }
    
    public void insert(String word) {
        Trie cur=this;
        for(int i=0;i<word.length();i++){
            char c=word.charAt(i);
            int index=c-'a';
            if(cur.children[index]==null){
                cur.children[index]=new Trie();
            }
            cur=cur.children[index];
        }
        cur.isEnd=true;
    }
    
    public boolean search(String word) {
        Trie last=existPrefix(word);
        return last!=null&&last.isEnd==true ? true:false;

    }
    
    public boolean startsWith(String prefix) {
        return existPrefix(prefix)!=null?true:false;
    }

    public Trie existPrefix(String prefix){
        Trie cur=this;
        for(int i=0;i<prefix.length();i++){
            char c=prefix.charAt(i);
            int index=c-'a';
            //中途就有字符不存在，匹配不上了
            if(cur.children[index]==null){
                return null;
            }
            cur=cur.children[index];
        }

        return cur;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

在这里插入图片描述
初始化时，前缀和为0的路径已经是一个了

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

//  利用前缀和的思想进行求解
class Solution {
    public int pathSum(TreeNode root, int targetSum) {
        HashMap<Long, Integer> prefix = new HashMap<>();
        prefix.put(0L, 1);
        return dfs(root, prefix, 0, targetSum);
    }


//利用好cur一直记录到当前节点至根节点之间的路径之和（一直更新hashmap数组，注意一定要按照路径添加）
    public int dfs(TreeNode root, Map<Long, Integer> prefix, long curr, int targetSum) {
        if(root==null){
            return 0;
        }

        int ret;//统计以本节点为末尾节点的targetsum满足的路径数量

        curr=curr+root.val;

        ret=prefix.getOrDefault(curr-targetSum,0);//判断有没有那样的前缀和（寻找头节点个数）
        
        prefix.put(curr,prefix.getOrDefault(curr,0)+1);//将包含当前节点的前缀和加入map中

        //继续自顶向下递归：寻找左右节点的情况
        ret=ret+dfs(root.left,prefix,curr,targetSum);
        ret=ret+dfs(root.right,prefix,curr,targetSum);

        //为了左子树的前缀和不影响右子树的判断，将当前的节点的前缀和减一(相当于一个回溯过程)
        prefix.put(curr,prefix.getOrDefault(curr,0)-1);

        return ret;



    }
}