正交矩阵； 实对称矩阵； 为什么实对称矩阵一定可以对角化； AB=0 r(A)+r(B)＜=n 证明； 初等矩阵； 初等矩阵的逆矩阵； 矩阵的左除右除；

 

目录

正交矩阵;

实对称矩阵;

为什么实对称矩阵一定可以对角化;

AB=0 r(A)+r(B)<=n 证明;

初等矩阵;

初等矩阵的逆矩阵;

矩阵的左除右除;

---

正交矩阵;

如果：AAT=E（E为单位矩阵，AT表示“矩阵A的转置矩阵”。）或ATA=E，则n阶实矩阵A称为正交矩阵，若A为正交阵，则:

 

1)逆也是正交阵 对于一个正交矩阵来说，它的逆矩阵同样也是正交矩阵。

2)积也是正交阵 如果两个矩阵均为正交矩阵，那么它们的乘积也是正交矩阵。

3)A的各行是单位向量且两两正交

4)A的各列是单位向量且两两正交

5)(Ax,Ay)=(x,y)x,y∈R

6)|A|=1或-1

7) 

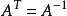
8)正交矩阵通常用字母Q表示。

实对称矩阵

如果有n阶矩阵A，其矩阵的元素都为实数，且矩阵A的