SLAM文献之-Probabilistic Degeneracy Detection for Point-to-Plane Error Minimization

背景与动机

• 点到平面误差最小化（Point-to-Plane ICP）是 LiDAR 定位与建图的核心步骤之一，却在 几何信息单一、环境退化（如隧道/平坦地面）时容易发生 退化（degeneracy）；
• 损失函数无法提供全部 6 DoF（姿态与位置）方向的约束，导致估计漂移；
• 现有做法多依赖 经验阈值 或 奇异值剔除，缺少统计一致性保障；
• 本文提出：概率建模 Hessian 噪声，评估某方向是否退化，并在 ICP 更新时适度抑制退化方向的更新，提高鲁棒性。
  *

---

摘要
几何信息不足导致的退化问题已知会严重影响基于 LiDAR 的定位与建图性能。本文提出了一种新的概率方法，用于在点到平面误差最小化过程中检测并缓解退化影响。我们从构造点到平面优化问题所使用的点与表面法线的噪声入手，对其海森矩阵的噪声进行了建模。基于此建模，我们能够量化某个方向是否发生退化的概率。

该退化检测方法被用于一个新的实时退化感知的迭代最近点（ICP）算法中，通过对退化方向的更新进行平滑衰减，实现更加鲁棒的 LiDAR 点云配准。该方法所需的参数根据 LiDAR 数据手册中提供的噪声特性进行设定。

在四组真实环境实验中对该方法进行了验证，结果表明，该方法在退化检测与影响缓解方面优于现有的最先进方法。

I. 引言

激光雷达（LiDAR）是众多同步定位与建图（SLAM）系统中的核心传感器类型 [1]–[5]。通常，系统通过迭代最近点（ICP）算法的各种变体，将当前帧的 LiDAR 点云配准到参考点云，并最小化几何代价函数 [6]。然而，在几何信息不足的环境中（例如结构自相似的隧道或圆柱形储罐）这一优化过程容易失败 [7]。在这些场景中，几何结构无法约束完整的六自由度（6-DoF）位姿，优化过程会在未被约束的方向上发生退化（degeneracy）。由于噪声可能引入虚假的约束信息，优化结果在这些方向上仍可能表现为过度自信却不准确。因此，若要实现可靠的状态估计，就必须显式地处理退化问题。

---

A. 相关工作

针对上述挑战，已有多个研究提出了不同的解决方法。文献 [8], [9] 提出了基于学习的方法来检测退化。虽然这些方法在训练完成后效果显著，但其对有标签的真实数据的依赖限制了其泛化能力。此外，较高的计算需求也使得它们难以在资源受限的系统上用于实时状态估计。

退化检测问题与基于 ICP 的配准中的协方差估计密切相关，已有解析法 [10], [11] 和数据驱动方法 [12], [13] 被提出用于该问题。然而，由于 ICP 协方差本身难以估计，因此仍需专门的退化检测方法。

开创性工作 [14] 从几何角度分析了退化问题。该方法通过设置几何代价函数 Hessian 矩阵特征值的阈值来检测退化情况，提出仅在非退化方向上更新估计的解重映射（solution remapping）技术。这一方法被多个主流 SLAM 框架采用，如 [4], [5]，并被认为是当前的技术基线。[15] 基于 [14] 扩展了适用于点到平面 ICP 的退化检测方法，并在因子图优化中引入了退化感知因子（degeneracy-aware factor），仅在非退化方向上起作用。此外，SLAM 框架 [16], [17] 也利用 Hessian 的条件数阈值来检测退化。这些方法虽然有效，但需要针对具体机器人、传感器、环境以及定位流程进行精细参数调优 [18]。

Hessian 特征值受到测量数量、加权方式、环境尺度以及传感器噪声等因素的影响，因此这些方法所需的参数难以在不同场景间泛化。[15], [19] 提出了动态参数调整方法用于改进 [14]，但这些方法仍未完全考虑特征值变化的所有来源，因此泛化能力有限。文献 [20] 所提出的可定位性指标（localizability metric）考虑了尺度因素，但该方法将 Hessian 分块处理（旋转块与平移块分别处理），因此当整体 Hessian 退化而分块未表现出退化时，可能会出现检测失败的情况。

---

B. 本文贡献

我们提出了一种通过对进入 Hessian 的噪声进行概率建模来检测退化的方法。该噪声建模被用于软退化分类（soft degeneracy classification），即通过信号与噪声之间的数量级差异，计算某个方向为有效非退化的概率。当信号至少比噪声大一个数量级时，该方向被认为是有效的。随后，我们将这种软分类用于概率退化感知的点到平面 ICP 中，在退化方向上对估计更新进行衰减处理。

由于该方法基于从一阶原理出发的概率建模，它可以显式考虑环境尺度、点权重以及测量数量等因素，并在这些维度上实现同时泛化，从而优于 [14]–[17]。基础噪声水平由用户根据点云和法线的噪声模型设置，我们依据激光雷达的数据手册来选择这些模型。因此，该方法可以明确考虑测量噪声和法线计算的不准确性。

与 [14] 类似，该方法是兼容实时处理的可插拔步骤，可无缝集成到常见的非线性最小二乘点到平面优化器中，且保持整体最坏情况的计算复杂度不变。我们将该方法集成进 SLAM 框架 [4]（该框架基于 LOAM [1] 进行 LiDAR 配准）实现实时状态估计。

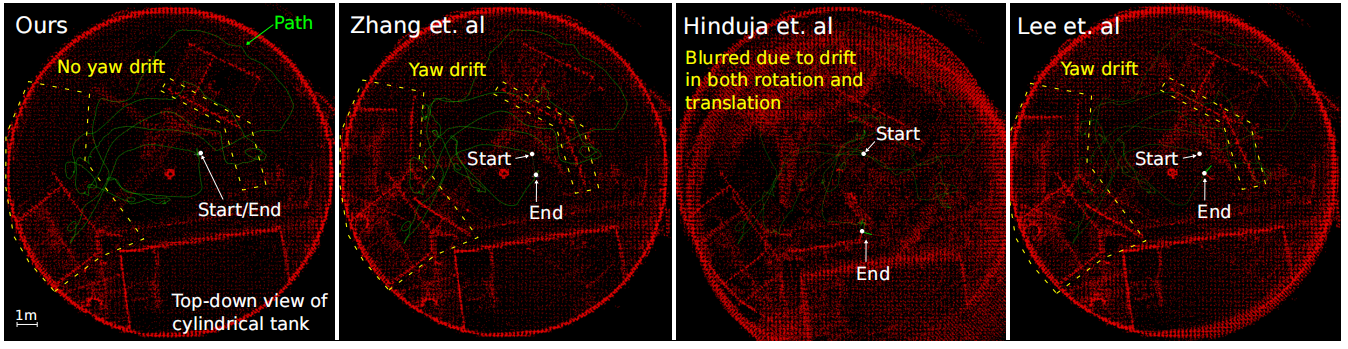
我们在四个由足式和飞行机器人在复杂环境中采集的真实数据集上验证了该方法，并与现有先进方法 [14], [15] 及近期方法 [19] 进行了对比。图 1 展示了典型的实验结果，附带的视频资料¹ 总结了方法与实验过程。

---

总体而言，本文的主要贡献如下：

1. 提出了一种适用于点到平面代价函数的新型概率建模退化检测方法，具备良好的泛化能力；
2. 提出了一种概率退化感知的点到平面 ICP 算法，用于实时 LiDAR 配准，可减弱退化方向上的噪声影响；
3. 在四个真实数据集上的实验验证了所提方法的有效性，优于已有方法 [14], [15], [19]；
4. 鉴于退化检测依赖于法线的协方差估计，我们还补充提出了一种实用的估计方法。

---

II. 预备知识与问题描述

本节将定义点到平面优化问题和噪声模型。随后，展示噪声如何在退化方向引入伪信息，从而引出问题定义。

A. 符号说明

• ∥x∥₂ 表示向量 x 的欧几里得范数。
• ∥x∥_S 表示马氏距离，其中 S 为正定矩阵。
• [a]× 表示向量 a ∈ ℝ³ 的反对称矩阵形式，满足 [a]×b = a × b，其中 × 表示向量叉乘。
• SO(3) 表示 3 阶特殊正交群。
• Exp(x) 表示如文献 [21] 中定义的指数映射。
• 矩阵以加粗的大写字母表示，如 H。H† 表示 H 的 Moore-Penrose 伪逆。I 表示单位矩阵。
• 𝒩(μ, Σ) 表示均值为 μ、协方差为 Σ 的多元正态分布。

---

B. 无噪声的点到平面优化

设有一组在激光雷达坐标系 L 中的无噪声点 $p^L\_i\in R^3$，以及对应的世界坐标系下无噪声平面 $(n\_i,d\_i)\in R^3\times R$，其中 $n\_i$ 是单位法向量，$d\_i$ 是从原点到平面的有符号垂直距离。

我们记 T = (R, t) 为激光雷达相对于世界坐标系的位姿估计，其中 R ∈ SO(3) 是旋转矩阵，t ∈ ℝ³ 是平移向量。
则点 $p^L\_i$ 在世界坐标系中的估计位置为 $p\_i=R{p}^L\_i+t$。

第 i 个点的点到平面误差为：

$$r_i(R,t)=n_i^T(R{p}_i^L+t)-d_i\text{\hspace{1em}(1)}$$

我们的目标是通过最小化点到平面的误差来求解 T：

$$\underset{R,t}{\min }\sum _{i=1}^N\rho (\Vert w_{ri}\cdot r_i(R,t){\Vert }^2)\text{\hspace{1em}(2)}$$

其中，ρ(u) 是 M-估计类的代价函数，例如标准的 L₂ 范数 $\rho (u)=u^2/2$，或者像 Geman-McClure 这样的亚二次鲁棒函数 $\rho (u)=\frac{u^2}{1+u^2}$。常见的鲁棒函数可参考文献 [22]。$w\_ri$ 是非负的标量权重。

根据文献 [23]，我们将公式 (2) 在线性化初始位姿 T 处，转换为最小二乘问题：

$$\underset{x}{\min }\sum _i\Vert J_{i}x-b_i{\Vert }_2^2\text{\hspace{1em}(3)}$$

其中：

• $J\_i=w\_i\left[\begin{array}{cc}(p\_i\times n\_i{)}^T& n\_i^T\end{array}\right]$
• $b\_i=-w\_i(n\_i^{T}p\_i-d\_i)$

优化变量 $x\in R^6$ 是李代数扰动量 $ x = [\delta r^T, \delta t^T]T$，其中 $\delta r$ 和 $\delta t$ 分别为旋转和位移扰动。

$w\_i$ 的定义为 $w\_i=w\_riw\_\rho \_i$，其中 $w\_\rho \_i$ 是由于选择代价函数而产生的误差衰减因子。
设 $u\_i=|w\_rir\_i{|}^2$，那么 $w\_{\rho \_i}^2={\rho }^{\prime }(u\_i)/u\_i$。例如，对于 L₂ 范数，$w\_{\rho \_i}^2=1$；对于 Geman-McClure，$w\_{\rho \_i}^2=(1+u\_i^2{)}^{-2}$。

通过求解以下线性系统获得最优扰动：

$$\left(\sum _i{J}_i^T{J}_i\right)x=\sum _i{J}_i^T{b}_i\text{\hspace{1em}(4)}$$

然后用指数映射更新位姿：

$$T\leftarrow \text{Exp}(x^{\ast })T$$

整个问题 (2) 可通过标准 ICP 方法求解：即在每次迭代中进行点-面关联、线性化当前位姿估计、求解最优扰动、并更新估计，直到满足终止条件。

令 H 表示优化问题的 Hessian 矩阵：

$$H=\sum _i{J}_i^T{J}_i=\sum _i{w}_i^2\left[\begin{array}{c}[p_i{]}_{\times }^T\\ I\end{array}\right]n_i{n}_i^T\left[\begin{array}{cc}[p_i{]}_{\times }& I\end{array}\right]\text{\hspace{1em}(5)}$$

退化意味着目标函数 (2) 在某些状态空间方向上不包含信息。换句话说，存在至少一个方向 $u$ 满足：

$$u^{T}Hu=0$$

此时，无噪声下扰动量的最小范数解为：

$$x^{\ast }={\left(\sum _i{J}_i^T{J}_i\right)}^{†}\left(\sum _i{J}_i^T{b}_i\right)\text{\hspace{1em}(6)}$$

对于任意退化方向 $u$，我们有 $u^T{x}^{}=0$，说明没有伪信息出现。然而在实际应用中，由于噪声，$x$ 的估计会受到伪信息干扰。

---

C. 噪声模型

我们假设点 ${\hat{p}}_i$ 受到加性高斯噪声的影响：

$${\hat{p}}_i=p_i+{ϵ}_i,{ϵ}_i\sim \mathcal{N}(0,{\Sigma }_{p_i})\text{\hspace{1em}(7)}$$

法向量被认为受到一个小的旋转扰动 ${\bar{R}}_i$ 的影响。利用小角度近似，可以写作：

$${\hat{n}}_i={\bar{R}}_i^T{n}_i\approx [I-[{\eta }_i{]}_{\times }]n_i=n_i+[n_i{]}_{\times }{\eta }_i\text{\hspace{1em}(8)}$$

其中 ${\eta }_i\sim \mathcal{N}(0,{\Sigma }_{n_i})$。所有的 ${\eta }_i$ 和 ${ϵ}_i$ 被假设为相互独立。

为了确保点、法向量以及点到平面的误差项满足高斯误差的假设，应根据需要使用鲁棒性措施，例如离群点剔除与鲁棒代价函数。关于 ICP 过程中的离群点过滤方法，请参见 [23] 中的综述。

D. 关于噪声引入的虚假信息

为了引出我们的方法，我们举例说明法向量上的噪声如何在 Hessian 中引入虚假信息。假设 ${\Sigma }_{n_i}={\sigma }_n^{2}I$，并且 ${\Sigma }_{p_i}\approx 0$。考虑法向量 ${\hat{n}}_i$ 代替 $n_i$ 后的正规方程（公式(4)）：

$$\sum _i{F}_i{\hat{n}}_i{\hat{n}}_i^T{F}_i^T\hat{x}=\sum _i{w}_i{F}_i{\hat{n}}_i{\hat{n}}_i^T(p_i-q_i)\text{\hspace{1em}(9)}$$

其中 $F_i^T=w_i\left[\begin{array}{cc}[p_i{]}_{\times }& I\end{array}\right]$，使得 $J_i={\hat{n}}_i^T{F}_i^T$。$q_i$ 是第 $i$ 个平面上的任意点。

对式 (9) 的两边应用条件期望 $\mathbb{E}[\cdot |\hat{x}]$，得到式子（10）：

$$\sum _i{F}_i\left[n_i{n}_i^T+{\sigma }_n^2(I-n_i{n}_i^T)\right]F_i^T\hat{x}=\sum _i{w}_i{F}_i\left[n_i{n}_i^T+{\sigma }_n^2(I-n_i{n}_i^T)\right](p_i-q_i)$$

我们进一步定义：

• $H_N={\sum }_i{\sigma }_n^2{F}_i(I-n_i{n}_i^T)F_i^T$
• $x_N=H_N^{†}{\sum }_i{\sigma }_n^2{w}_i{F}_i(I-n_i{n}_i^T)(p_i-q_i)$

那么，式 (10) 可重写为：

$$(H+H_N)\hat{x}=H{x}^{\star }+H_N{x}_N\text{\hspace{1em}(11)}$$

因此，我们可以预期估计扰动 $\hat{x}$ 是无噪声扰动 $x^{\star }$ 和一个偏差项 $x_N$ 的加权平均。如果 $H\gg H_N$，那么 $\hat{x}\approx x^{\star }$，这正是我们想要的情况。但另一方面，如果几何结构无法提供有效信息，使得无噪声 Hessian 在某方向 $u$ 上是退化的，即：

$$u^{T}Hu=0$$

那么 $u^T\hat{x}$ 完全来源于噪声。同样地，当 $H_N$ 在方向 $u$ 上的虚假信息 $u^T{H}_{N}u$ 超过了真实信息 $u^{T}Hu$ 时，我们也认为 $u^T\hat{x}$ 是不可靠的。

通过检测并抑制这些噪声主导信号的方向，可以降低由 $x_N$ 带来的噪声偏差。这正是我们所采用的方法。

---

E. 问题表述

基于以上讨论，本文要解决以下两个核心问题：

1. 退化方向的识别与量化：
   给定带噪声的点到平面 Hessian $\hat{H}$ 以及用于构造它的点和法向量的噪声模型，估计噪声对 $\hat{H}$ 的影响，并量化某个方向 $u$ 在 $\hat{H}$ 中是退化的概率。

2. 基于退化概率的优化改进：
   利用退化概率，减少在被认为退化的方向上噪声引起的虚假信息，从而改进点到平面的优化过程。

---

III. 方法

A. 概率退化检测（Probabilistic Degeneracy Detection）

概率退化检测的目标是量化海森矩阵（Hessian）在任意方向 $u\in {\mathbb{R}}^6$ 上退化的概率。为此，我们估计噪声对海森矩阵的影响，并评估一个信噪比（Signal-to-Noise Ratio，SNR）。

带噪的海森矩阵 $\hat{H}$ 表示为向量外积的总和：

$$\hat{H}=\sum _i{\hat{v}}_i{\hat{v}}_i^T,{\hat{v}}_i=w_i\left[\begin{array}{cc}[{\hat{p}}_i{]}_{\times }& I\end{array}\right]{\hat{n}}_i\text{\hspace{1em}(12)}$$

外积的噪声特性由其构成向量的噪声特性决定。将噪声模型（公式 (7)-(8)）代入 $\hat{v}\_i$，可得式子（13）：

$${\hat{v}}_i=v_i+w_i\underset{B_i}{\underbrace{\left[\begin{array}{cc}-[n_i{]}_{\times }[p_i{]}_{\times }[n_i{]}_{\times }& 0\\ 0& [n_i{]}_{\times }\end{array}\right]}}\left[\begin{array}{c}{\eta }_i\\ {ϵ}_i\end{array}\right]+w_i[{ϵ}_i{]}_{\times }[n_i{]}_{\times }{\eta }_i,v_i=w_i\left[\begin{array}{cc}[p_i{]}_{\times }& I\end{array}\right]n_i$$

$\hat{v}\_i$ 的期望和协方差分别为式子（14）：

$$\mathbb{E}[{\hat{v}}_i]=v_i,{\Sigma }_i=\text{cov}({\hat{v}}_i)=B_i\left[\begin{array}{cc}\mathbb{E}[{ϵ}_i{ϵ}_i^T]& 0\\ 0& \mathbb{E}[{\eta }_i{\eta }_i^T]\end{array}\right]B_i^T$$

因此，带噪海森矩阵的期望为式子（15）：

$$\mathbb{E}[\hat{H}]=\sum _i\mathbb{E}[{\hat{v}}_i{\hat{v}}_i^T]=\sum _i{v}_i{v}_i^T+\sum _i\text{cov}({\hat{v}}_i)=H+\Sigma ,\Sigma :=\sum _i\text{cov}({\hat{v}}_i)$$

也就是说，从期望上来看，H 被协方差项 $\Sigma$ 扰动了。

我们在单位向量方向 $|u|=1$ 上计算 $\hat{H}$ 的方差为：

$${\sigma }_u^2=\text{cov}(u^T\hat{H}u)=\sum _i\text{cov}(u^T{\hat{v}}_i{\hat{v}}_i^{T}u)\text{\hspace{1em}(16)}$$

由于 $\text{cov}(u^T\hat{v}\_i\hat{v}\_i^{T}u)=\text{cov}(\hat{v}\_i^{T}u{u}^T\hat{v}\_i)$，我们使用 [24] 中关于二次型方差的表达式，有：

$$\text{cov}(u^T{\hat{v}}_i{\hat{v}}_i^{T}u)=2(u^T{\Sigma }_{i}u{)}^2+4(u^T{\Sigma }_{i}u)(u^T{v}_i{)}^2\text{\hspace{1em}(17)}$$

注意，如果 $\hat{v}\_i$ 是具有单位方差的标量，那么 (15) 和 (16) 就分别对应**非中心卡方分布（non-central chi-squared distribution）**的均值与方差 [25]。

使用公式 (15)-(16) 中的期望与方差来量化某个方向上退化的可能性。由于在实际中我们无法获取真实点和法向量，我们使用其带噪版本估计 $\Sigma \_i$、$\Sigma$ 和 $\sigma \_u^2$，分别记作 $\hat{\Sigma }\_i$、$\hat{\Sigma }$ 和 $\hat{\sigma }\_u^2$。

令 $\xi \_u$ 表示方向 $u$ 上的噪声，并假设其服从高斯分布：

$${\xi }_u\sim \mathcal{N}({\hat{\mu }}_u,{\hat{\sigma }}_u^2),\text{其中}$$

$${\hat{\mu }}_u=u^T\hat{\Sigma }u\text{\hspace{1em}(18)}$$

$${\hat{\sigma }}_u^2=\sum _i\left[2(u^T{\hat{\Sigma }}_{i}u{)}^2+4(u^T{\hat{\Sigma }}_{i}u)(u^T{\hat{v}}_i{)}^2\right]\text{\hspace{1em}(19)}$$

同时，设 $a\_u=u^{T}Hu$，$\hat{a}\_u=u^T\hat{H}u$，我们有：

$${\hat{a}}_u=a_u+{\xi }_u$$

此时，$a\_u/\xi \_u$ 可被视为方向 $u$ 上的信噪比。

如第二节所述，若某一方向上的信号 $a\_u$ 显著大于噪声 $\xi \_u$，则该方向是可可靠估计的。因此，我们定义信号比噪声大 $s$ 倍的概率为：

$$p_u=\mathbb{P}(a_u\ge s{\xi }_u)=\mathbb{P}({\hat{a}}_u\ge (s+1){\xi }_u)\text{\hspace{1em}(20)}$$

关于如何选择 $s$，考虑相对误差 $e\_u^{rel}=(\hat{a}\_u-a\_u)/a\_u=\xi \_u/a\_u$。如果 $a\_u\ge s\xi \_u$，则 $e\_u^{rel}\le s^{-1}$。因此，我们设置 $s = 10$，使得目标相对误差不超过 10%。一般而言，增大 $s$ 会使退化检测更保守。

如果 $p\_u\approx 0$，我们就认为方向 $u$ 是退化的；如果 $p\_u\approx 1$，则方向 $u$ 是非退化的。

从公式 (12)-(15) 可以看出，海森矩阵中引入的噪声依赖于：

• 测量数量 $N$，
• 权重 $w\_i$，
• 点与法向的噪声（来自公式 (7)-(8)），
• 以及通过叉乘项
  $$[\hat{p}\ast i]\ast \times \hat{n}\_i$$
  体现的环境尺度。
  与先前方法 [14]–[17], [20] 不同，本文中定义的概率 $p\_u$（见公式 (20)）同时考虑了上述所有因素，实现了更全面的退化检测。

---

B. 概率退化感知的 ICP（Probabilistic Degeneracy-Aware ICP）

概率退化感知的 ICP 旨在通过减少退化方向上虚假信息的影响来改进点到平面 ICP [26]。我们将讨论限制在对标准点到平面 ICP 所做的具体修改上，更完整的 ICP 点云配准流程请参见 [23]。

类似于 [14]、[15]，我们调整了 ICP 算法的更新步骤。

作为动机，我们重新审视第 II-B 节中讨论的无噪声情形，特别是考虑矩阵 H 的 Moore-Penrose 伪逆。利用对角化表示 H = UΛUᵀ，其中 U = [u₁, ···, u₆] 是一个正交矩阵，满足 UᵀU = I，Λ = diag(λ₁, ···, λ₆)。H 的 Moore-Penrose 伪逆为 H† = UΛ†Uᵀ，其中 Λ† = diag(λ†₁, ···, λ†₆)，并且：

$${\lambda }_k^{†}=\{\begin{array}{ll}\frac{1}{{\lambda }_k},& {\lambda }_k>0\\ 0,& {\lambda }_k=0\end{array}\text{\hspace{1em}(21)}$$

当方向 uₖ 为退化方向时，对应的 λₖ 和 λₖ† 为 0。因此，使用式 (6) 中的最小范数扰动解 $x^{\star }$，可以确保退化方向保持不变，即：

$$u_k^T{x}^{\star }=0\text{当}{\lambda }_k=0。$$

为了应对噪声，我们定义了一个修改后的伪逆。假设噪声扰动下的 Hessian 为 $\hat{H}=\hat{U}\hat{\Lambda }{\hat{U}}^T$。由于噪声的存在，当 $N\ge 6$ 时，$\hat{H}$ 的所有特征值以概率 1 都不为零，因此式 (21) 便不再适用。

我们引入一个指示变量 Ik∈{1,0}I_k ∈ \{1, 0\}Ik​∈{1,0}，当方向 ${\hat{u}}_k$ 被判断为退化方向时令 $I_k=0$，否则为 1。然后，我们将式 (21) 替换为：

$${\hat{\lambda }}_k^{‡}=I_k\cdot \frac{1}{{\hat{\lambda }}_k}+(1-I_k)\cdot 0\text{\hspace{1em}(22)}$$

[14] 和 [15] 采用固定阈值的方法来确定所有特征值的退化性，即当 ${\hat{\lambda }}_k>{\lambda }_{\min }$ 时认为该方向非退化（即 $I_k=1$），这本质上是对 $\hat{H}$ 进行截断奇异值分解（SVD）[27]。

在我们的方法中，我们使用第 III-A 节提出的概率退化检测方法，为每个特征方向 ${\hat{u}}_k$ 提供其为退化方向的概率。我们对式 (22) 关于 $I_k$ 取期望值，使用式 (20) 的概率来得到：

$${\hat{\lambda }}_k^{+}={\mathbb{E}}_{I_k}[{\hat{\lambda }}_k^{‡}]={\mathbb{E}}_{I_k}\left[I_k\cdot \frac{1}{{\hat{\lambda }}_k}\right]=p_{{\hat{u}}_k}\cdot \frac{1}{{\hat{\lambda }}_k}\text{\hspace{1em}(23)}$$

这个表达式（23）平滑地反映了退化与非退化之间的过渡。令 $J^T=[J_1^T,\cdots ,J_N^T]$，$b^T=[b_1,\cdots ,b_N{]}^T$，$\hat{J},\hat{b}$ 为其含噪版本。

使用式 (23)，我们可估计扰动项为：

$${\hat{x}}^{\star }=\hat{U}P{\hat{\Lambda }}^{-1}{\hat{U}}^T{\hat{J}}^T\hat{b}\text{\hspace{1em}(24)}$$

其中 $P=\text{diag}(p_{{\hat{u}}_1},\cdots ,p_{{\hat{u}}_6})$。

从最小二乘的角度来看，这等价于在点到平面代价函数中降低信息量，并在 $p_{{\hat{u}}_k}<1$ 的方向上引入零先验。为更清楚地理解，考虑 $\hat{J}=\hat{V}\hat{S}{\hat{U}}^T$，其中 ${\hat{S}}^T\hat{S}=\hat{\Lambda }$，并定义：

$$W^{1/2}=\hat{V}\cdot \text{diag}(P^{1/2},I_{N-6})\cdot {\hat{V}}^T\text{\hspace{1em}(25)}$$

我们要最小化如下代价函数：

$$\Vert W^{1/2}\hat{J}\hat{x}-W^{1/2}\hat{b}{\Vert }_2^2+\Vert (I-P{)}^{1/2}{\hat{\Lambda }}^{1/2}{\hat{U}}^T\hat{x}{\Vert }_2^2\text{\hspace{1em}(26)}$$

其最小值解为满足下式的 $\hat{x}$：

$$\hat{U}[P\hat{\Lambda }+(I-P)\hat{\Lambda }]{\hat{U}}^T\hat{x}={\hat{J}}^T\hat{J}\hat{x}=\hat{U}P{\hat{U}}^T{\hat{J}}^T\hat{b}\text{\hspace{1em}(27)}$$

左乘 $({\hat{J}}^T\hat{J}{)}^{-1}={\hat{H}}^{-1}$ 可得与式 (24) 相同的解。

矩阵 $W$ 实际上放大了点到平面误差的协方差。而式 (26) 中的零先验则是一个 Tikhonov 正则项 [27]，它通过在退化方向上惩罚扰动幅度来解决原始优化问题的病态性。

从最小二乘解释出发，我们可估计扰动解 ${\hat{x}}^{\star }$ 的信息矩阵（即协方差的逆）为：

$${\hat{\Lambda }}_{\hat{x}}=\frac{1}{{\sigma }_r^2}\hat{U}P\hat{\Lambda }{\hat{U}}^T\text{\hspace{1em}(28)}$$

其中 ${\sigma }_r^2$ 是点到平面残差的方差估计。注意，在公式 (28) 中我们忽略了正则项的信息。当 $p_u=0$ 时，$u^T{\hat{\Lambda }}_{\hat{x}}u=0$，反映了在退化方向上缺乏信息（即方差趋于无穷）。

该方法总结如下算法 1 所示。此算法成功地降低了来自退化方向的虚假信息影响，具体表现为若 $p_{{\hat{u}}_k}\approx 0$，则 ${\hat{u}}_k^T{\hat{x}}^{\star }\approx 0$，而非退化方向（$p_{{\hat{u}}_k}\approx 1$）则保持不变。相比于标准点到平面 ICP，每次更新增加的计算复杂度为 $O(N)$，主要来自对每个方向 $k=1,\dots ,6$ 计算 ${\hat{\mu }}_{{\hat{u}}_k},{\hat{\sigma }}_{{\hat{u}}_k},p_{{\hat{u}}_k}$。因此，该算法的最坏情况复杂度与标准点到平面 ICP 相同，适用于实时应用。

---

算法 1：退化感知 ICP 的更新步骤

输入：

{p^i,n^i,d^i,wri,Σpi,Σni}i=1,...,N \{ \hat{p}_i, \hat{n}_i, \hat{d}_i, w_{ri}, Σ_{p_i}, Σ_{n_i} \}_{i=1,...,N} {p^​i​,n^i​,d^i​,wri​,Σpi​​,Σni​​}i=1,...,N​

输出：

$${\hat{x}}^{\star }$$

1. 计算 Hessian 矩阵 $\hat{H}$ 及右侧向量 ${\sum }_i{\hat{J}}_i^T{\hat{b}}_i$

2. 对 Hessian 进行对角化分解：$\hat{H}=\hat{U}\hat{\Lambda }{\hat{U}}^T$

3. 对每个方向 $k=1,\dots ,6$，计算 ${\hat{\mu }}_{{\hat{u}}_k},{\hat{\sigma }}_{{\hat{u}}_k},p_{{\hat{u}}_k}$

4. 计算更新量：

   $${\hat{x}}^{\star }\leftarrow \hat{U}P{\hat{\Lambda }}^{-1}{\hat{U}}^T\sum _i{\hat{J}}_i^T{\hat{b}}_i$$

5. 返回 ${\hat{x}}^{\star }$

---

C. 法向量的协方差估计

为了在实际中使用我们的退化感知 ICP 算法，我们必须估计法向量的协方差。这里我们提供一种直接的方法来实现这一点。

设 Qi={q^il}l=0,…,NiQ_i = \{\hat{q}_{il}\}_{l=0,\ldots,N_i}Qi​={q^​il​}l=0,…,Ni​​ 是用于估计第 $i$ 个法向量的 $N_i$ 个点的集合。假设每个点 ${\hat{q}}_{il}$ 都受到各向同性的高斯噪声影响，

$${\hat{q}}_{il}=q_{il}+{ϵ}_{il},{ϵ}_{il}\sim \mathcal{N}(0,I{\sigma }_i^2)\text{\hspace{1em}(29)}$$

所有的 ${ϵ}_{il}$ 被认为是相互独立的。令 ${\bar{\hat{q}}}_i$ 表示点集 $Q_i$ 的经验均值。该点集的经验协方差为：

$${\hat{C}}_i=\frac{1}{N_i-1}\sum _l({\hat{q}}_{il}-{\bar{\hat{q}}}_i)({\hat{q}}_{il}-{\bar{\hat{q}}}_i{)}^T\text{\hspace{1em}(30)}$$

法向量估计 ${\hat{n}}_i$ 是通过取协方差矩阵 (30) 的最小特征值所对应的特征向量得到的，正如最初在 [28] 中提出的那样。我们通过考虑一个相关的最小二乘问题来对每个 ${\hat{n}}_i$ 的协方差进行估计。设 ${\hat{n}}_i={\hat{R}}_i{e}_z$ 为我们对第 $i$ 个法向量的估计，其中 ${\hat{R}}_i\in SO(3)$ 是某个旋转矩阵，$e_z=[0,0,1{]}^T$。

${\hat{R}}_i$ 是下面这个非线性最小二乘问题的最优解：

$$\underset{R_i\in SO(3)}{\min }\sum _l{\Vert ({\hat{q}}_{il}-{\bar{\hat{q}}}_i{)}^T{R}_i{e}_z\Vert }^2=\frac{N_i-1}{N_i}{\sigma }_i^2\text{\hspace{1em}(31)}$$

等价形式为：

$$\underset{R_i\in SO(3)}{\min }\frac{1}{{\sigma }_i^2/N_i}{\Vert {\hat{C}}_i^{1/2}{R}_i{e}_z\Vert }^2$$

对上述优化问题进行对角化，即将协方差矩阵表示为 ${\hat{C}}_i={\hat{R}}_i{\hat{\Lambda }}_i{\hat{R}}_i^T$，其中 ${\hat{\Lambda }}_i=\text{diag}({\hat{\lambda }}_{i1},{\hat{\lambda }}_{i2},{\hat{\lambda }}_{i3})$，特征值按从大到小排列，并且 ${\hat{R}}_i\in SO(3)$。可以证明 ${\hat{R}}_i$ 是问题 (31) 的最优解。

我们使用线性化优化问题的 Hessian 来估计协方差。对旋转矩阵进行小角度近似线性化 $[I+[{\nu }_i{]}_{\times }]R_i$，得到在 $R_i={\hat{R}}_i$ 处的雅可比矩阵：

$${\hat{J}}_{n_i}=-{\hat{C}}_i^{1/2}[{\hat{n}}_i{]}_{\times }\sqrt{\frac{1}{{\sigma }_i^2/N_i}}\text{\hspace{1em}(32)}$$

对应的 Hessian 为：

$${\hat{J}}_{n_i}^T{\hat{J}}_{n_i}=\frac{1}{{\sigma }_i^2/N_i}{\hat{R}}_i\text{diag}({\hat{\lambda }}_{i2},{\hat{\lambda }}_{i1},0){\hat{R}}_i^T\text{\hspace{1em}(33)}$$

其伪逆即为法向量 ${\hat{n}}_i$ 的协方差估计：

$${\hat{\bar{\Sigma }}}_{{\hat{n}}_i}=({\hat{J}}_{n_i}^T{\hat{J}}_{n_i}{)}^{†}={\hat{R}}_i\frac{{\sigma }_i^2}{N_i}\text{diag}\left(\frac{1}{{\hat{\lambda }}_{i2}},\frac{1}{{\hat{\lambda }}_{i1}},0\right){\hat{R}}_i^T\text{\hspace{1em}(34)}$$

符合直觉的是，当点集 $Q_i$ 在正交于法向量 ${\hat{n}}_i$ 的方向上分布较窄时，法向量的不确定性更大。由于法向量限定在单位球面上，其在方向 ${\hat{n}}_i$ 上的方差为零。

可以证明式 (34) 等价于：

$${\Sigma }_{{\hat{n}}_i}=[{\hat{n}}_i{]}_{\times }\frac{{\sigma }_i^2}{N_i}{\hat{C}}_i^{-1}[{\hat{n}}_i{]}_{\times }^T$$

为了与之前的噪声模型 (8) 一致，我们采用如下形式的估计：

$${\hat{n}}_i\approx n_i+[{\hat{n}}_i{]}_{\times }{\eta }_i,{\eta }_i\sim \mathcal{N}(0,\frac{{\sigma }_i^2}{N_i}{\hat{C}}_i^{-1})\text{\hspace{1em}(35)}$$

估计法向量及其协方差的计算复杂度为 $\mathcal{O}(N_i)$，但协方差估计 (35) 本身仅增加了 $\mathcal{O}(1)$ 的额外开销。因此，协方差估计是表面法向量估计过程中的一个计算代价低廉的副产品。

我们还利用该协方差估计进行异常值剔除。根据公式 (34)，最坏情况下的方差 ${\max }_{\Vert u{\Vert }^2=1}{u}^T{\hat{\bar{\Sigma }}}_{{\hat{n}}_i}u$ 为：

$${\sigma }_{{\hat{n}}_i}^2=\frac{{\sigma }_i^2}{N_i}\frac{1}{{\hat{\lambda }}_{i2}}$$

若满足 ${\sigma }_{{\hat{n}}_i}^2>{\sigma }_{n,\text{max}}^2$，则将法向量 ${\hat{n}}_i$ 判定为异常值，其中 ${\sigma }_{n,\text{max}}^2>0$ 是用户设定的阈值。

IV. 实验

本文提出的方法在四个数据集上进行了评估，这些数据集使用了足式机器人和空中机器人，并处于具有挑战性的环境中。

---

A. 实现与参数选择

第 III 节中的方法被集成到了 CompSLAM 框架中 [4]。该框架在处理 LiDAR 数据时依赖于 LOAM 方法 [1]。我们对 LOAM 的建图模块进行了如下调整：

1. 用算法 1 替换了 LOAM 中的 ICP 更新步骤；
2. 仅使用平面特征；
3. 使用第 III-C 节的方法估计每个法向量的协方差。

对于协方差大于 σₙ²^max = 0.1² 的特征（即 σ̂ₙ²ᵢ > σₙ²^max），将其视为离群点并剔除。算法 1 的所有输入都以局部 LiDAR 坐标系表示。我们使用伴随变换（详见 [21]）将计算出的局部扰动转换为世界坐标系中的扰动。LOAM 的里程计模块被绕过，LiDAR 建图所需的先验信息由外部里程计源提供。

我们在同一框架下实现了文献 [14]、[15] 中的先进方法以及近期方法 [19]，以作对比。文献 [14] 的方法需要一个样本数据集来进行参数调优，其参数按照 [14] 中的方法为每个平台调优一次。而我们的方法仅根据 LiDAR 数据表为每个平台选择一次参数。

实验 1、3 和 4 的数据集缺乏真实轨迹，因此我们为所有实验提供了定性结果，并仅在实验 2 中给出定量评估。

B. 实验 1 - 瑞士鲁姆朗（Rümlang）建筑工地

我们展示了本文方法应对旋转与平移退化（degeneracy）情况的能力。

Rümlang Construction Site 数据集由 ANYbotics 的 ANYmal C 足式机器人 [29] 在瑞士 Rümlang 地区采集。机器人在建筑工地中的一个开阔区域内移动，并在图 2 中 A 和 B 两个位置原地旋转。当可见信息仅来自地面平面时，沿地面平面的平移和绕地面法向的旋转将处于欠约束状态。机器人搭载的是 Velodyne VLP-16 LiDAR（10 Hz）。若使用 LiDAR 的完整 360° 视场（FOV），scan-to-map ICP 仅会轻微受到退化影响。因此，为了使用该数据集更好地研究退化情形，我们将激光雷达的水平视场人为缩减至 180°，以增加估计难度。

我们使用足式机器人的里程计作为 LiDAR 建图模块的先验信息来源。根据 Velodyne VLP-16 的参数表，我们设置：

1. 各点使用各向同性且均匀的噪声模型，$\Sigma \_p\_i=\sigma \_p^{2}I$，其中 $\sigma \_p=1$ cm；
2. 在法向协方差估计过程中设置 $\sigma \_i=1$ cm。

参数完全依据理论原理选取，未在该数据集上进行实验性调参。而文献 [14] 中的方法，我们根据实验调参设定 $\lambda \_\text{min}=24$。

结果可视化如图 2 所示，定性总结见表 I。与其他方法在退化区域出现明显漂移不同，我们的方法未出现此类漂移。

---

C. 实验 2 - 瑞士 Seemühle 矿井

我们展示了本文方法在一个平移退化环境中的泛化能力，平台与实验 1 相同。

Seemühle Mine 数据集由 ANYbotics 的 ANYmal C 机器人在瑞士一个废弃矿井中采集。机器人在一个结构重复的隧道中往返运动。在大部分隧道段中，纵向平移处于退化状态（不可观）。

我们在该实验中使用 Velodyne VLP-16 LiDAR（10 Hz）全 360° 视场。此外，使用一台正前方朝向的 0.4 MP 单色灰度相机（20 Hz）和 IMU（200 Hz），来自 Sevensense Robotics 的 Alphasense 开发套件。通过 ROVIO [30] 实现视觉-惯性里程计，用于提供 LiDAR 建图模块的先验信息。真实轨迹通过文献 [20] 中的方法生成。使用文献 [31] 的工具计算估计轨迹相对于真值的绝对位姿误差（APE）与相对位姿误差（RPE）。

由于 LiDAR、机器人平台与整体配准流程与实验 1 相同，我们在实验 2 中继续沿用相同参数。对于文献 [14]，由于视场加倍，我们将阈值加倍为 $\lambda \_\text{min}=48$。

结果可视化如图 3 所示，定性与定量评估结果分别汇总在表 I 和表 II 中。我们的方法与 [15] 在非隧道段（即隧道前后）轨迹上的 APE 表现相当，且未出现明显的退化导致的漂移。而 [14] 和 [19] 的较高 APE 源于图 3 所示的退化导致的平移漂移。我们的算法在整体 APE 表现中最低，并且无需更改参数即可从实验 1 泛化至实验 2。若给予文献 [14] 的方法以数据集级别的调参优势（调至 $\lambda \_\text{min}=150$），其定性表现才可与我们的方法相当。

---

表 I：退化引起的漂移的定性评估

实验编号	数据集	本文方法	Zhang [14]	Hinduja [15]	Lee [19]
1	Rümlang 建筑工地	✓	×	×	×
2	Seemühle 矿井	✓	×	✓	×
3	Relyon 工业现场	✓	×	×	×
4	Fyllingsdalen 隧道	✓	×	✓	×

注：✓ 表示未发生退化引起的漂移，× 表示发生漂移。

V. 结论

在复杂环境中进行可靠的基于 LiDAR 的定位与建图，识别和处理退化问题至关重要。本文提出了一种新的概率方法，用于在点到平面误差最小化问题中检测退化情形，并提出了一种概率退化感知的迭代最近点（ICP）算法。

在四个真实世界的复杂环境实验中，该方法在应对退化影响方面优于现有的先进方法。由于其基于一阶原理的建模方式，本文方法相比基线方法具有更简便的参数选择过程和更强的泛化能力。