动态规划（一）

前言

因为快要找工作了，最近一直在刷算法题，在做算法题时遇到了不少关于动态分布的问题。以前接触过关于动态规划的问题不多，这让我很头疼，在看了些文档和教学视频后对此有了一部分的理解。这里我通过博客的方式来将我的心得分享出来，来记录我的成长。

什么是动态规划？

动态规划程序设计是对解最优化问题的一种途径、一种方法，而不是一种特殊算法。不像搜索或数值计算那样，具有一个标准的数学表达式和明确清晰的解题方法。动态规划程序设计往往是针对一种最优化问题，由于各种问题的性质不同，确定最优解的条件也互不相同，因而动态规划的设计方法对不同的问题，有各具特色的解题方法，而不存在一种万能的动态规划算法，可以解决各类最优化问题。

斐波那契数列

今天先举一个简单的例子来接触动态规划。
斐波那契数列大家很熟悉，第n个数等于第n-1和第n-2个数之和，f(n)=f(n-1)+f(n-2)，我们一般编程时会首先想到用递归的方法解决。如下：

// C#实现
static void Main()
{
	Console.WriteLine("请输入你要求第几个数：");
    int num = int.Parse(Console.ReadLine());
    if (num <= 0)
        Console.WriteLine(num);
    else
        Console.WriteLine(result(num));
    Console.Read();
}
static int result(int num)
{
	if (num == 1 || num == 2)
		return 1;
	return result(num - 1) + result(num - 2);
}

但是这样写有个问题，时间复制度太大，为O(2^n)，如果要求的数很大就会很吃时间和资源，为什么会这样呢？请看下面的图：

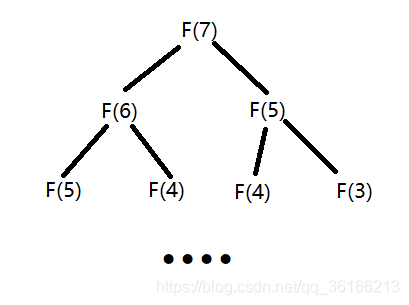
如上图所示，在运算过程中F(5)的运算存在重复运算的现象，这样运算时间就会乘2，F(4)、F(3)也存在相同的问题，运算时间不断乘2，最终时间复制度会达到O(2^n)。很明显已经计算过的不需要再次进行运算了，我们可以在把计算过的值在内存中保留一份，这样当我们再次要用到它时直接从内存中调出来，就可以节省时间，时间复制度便只有O(n)。

自顶而下

static void Main()
{
	Dictionary<int, int> index_num = new Dictionary<int, int>();
	Console.WriteLine("请输入你要求第几个数：");
	int num = int.Parse(Console.ReadLine());
	if (num <= 0)
		Console.WriteLine(num);
	else
		Console.WriteLine(result(num, index_num));
	Console.Read();
}
static int result(int num, Dictionary<int, int> index_num)
{
	int num1, num2;
	if (num <= 2)
		return 1;
	if (index_num.ContainsKey(num - 1))
		num1 = index_num[num - 1];
	else
	{
	 	num1 = result(num - 1, index_num);
		index_num.Add(num - 1, num1);
	}
	if (index_num.ContainsKey(num - 2))
		num2 = index_num[num - 2];
	else
	{
		num2 = result(num - 2, index_num);
		index_num.Add(num - 2, num2);
	}
	return num1 + num2;
}

但是上面这段代码用的还是递归的方法，自顶到下来计算，那我们为何不自底到上的来进行计算呢？这也是动态分布的核心思想。

自底而上

static void Main()
{
	Console.WriteLine("请输入你要求到第几个数：");
	int num = int.Parse(Console.ReadLine());
	if (num <= 1)
		Console.WriteLine(num);
	else
	{
		int[] index_num = new int[num + 1];
		index_num[0] = 0;
		index_num[1] = 1;
		for (int i = 2; i < num + 1; i++)
			 index_num[i] = index_num[i - 1] + index_num[i - 2];
		for (int i = 1; i < num + 1; i++)
			Console.WriteLine(index_num[i]);
	}
	Console.Read();
}

从上面的例子可以看到自顶向下的方式的动态规划其实包含了递归，而递归就会有额外的开销的；而使用自底向上的方式可以避免。