回溯算法
实际上就是一个决策树的遍历过程:
- 路径:就是已经做出的选择
- 选择列表:就是你当前可以做的选择
- 结束条件:就是到达决策树底层,无法再做选择的条件
回溯算法的框架(伪代码)
result = []
def backtrack(路径,选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径,选择列表)
撤销选择
解题思路
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例:
输入:s = “abc”
输出:[“abc”,“acb”,“bac”,“bca”,“cab”,“cba”]
解题思路
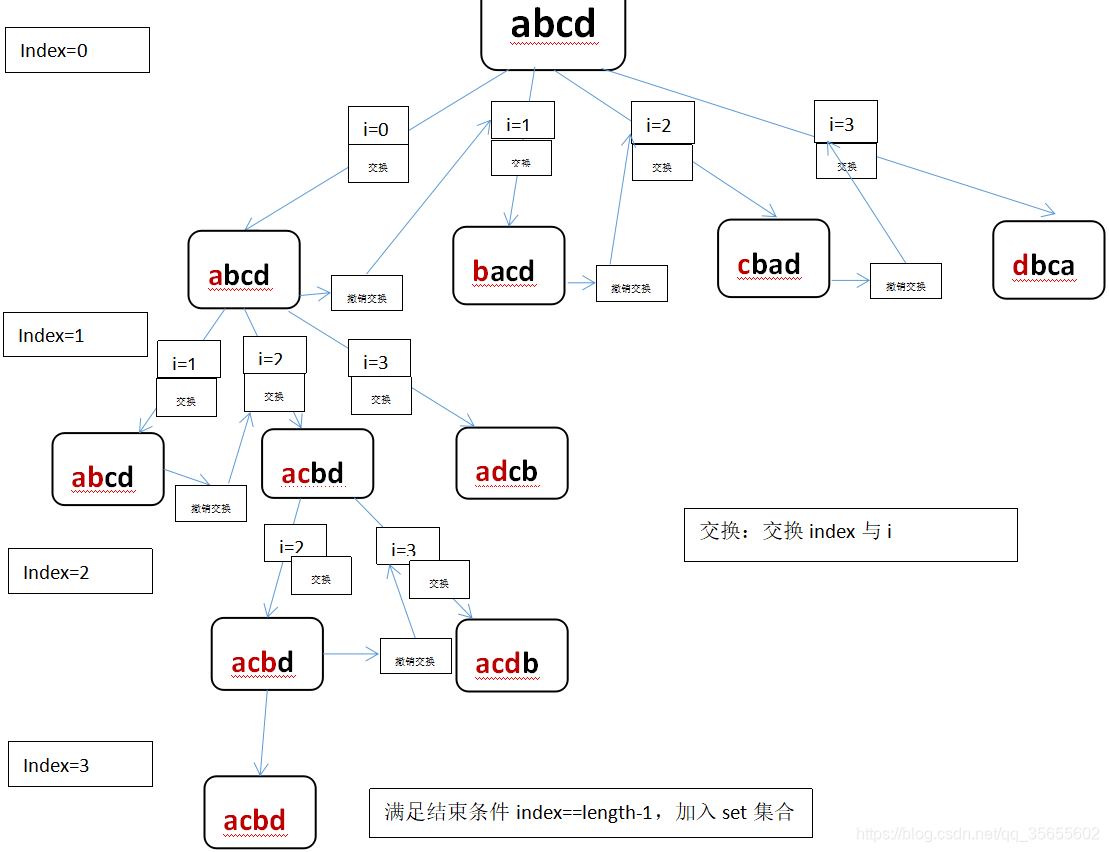
回溯法题目无非就是穷举所有可能,我们对字符串中的字符进行两两交换,可以得到所有结果,难点在于,有些字符会重复出现,所以这样得到的字符串也会重复。
要去重复,可以用set容器来存储得到的结果,最后返回结果集的数组形式即可。
class Solution_38_1 {
public String[] permutation(String s) {
Set<String> res = new HashSet<>();
char[] C = s.toCharArray();
backtrack(0,C,res);
//遍历集合,将答案放入数组中进行输出
String[] ans = new String[res.size()];
int i = 0;
for (String str : res) {
ans[i++] = str;
}
return ans;
}
private void backtrack(int index, char[] S, Set<String> res) {
if (index == S.length - 1){//结束判断条件
res.add(String.valueOf(S));
return;
}
for(int i = index;i<S.length;i++){//可选择的方案
swap(index,i,S);//做出选择
backtrack(index + 1,S,res);//进行下一步
swap(index,i,S);//撤销选择
}
}
private void swap(int i, int j, char[] C) {//数组元素的交换
char temp = C[i];
C[i] = C[j];
C[j] = temp;
}
}








 本文介绍了如何使用回溯算法解决剑指 Offer 38 题目,即找出字符串的所有排列。通过建立决策树并遍历,避免重复,利用 set 存储唯一结果,最终返回排列数组。
本文介绍了如何使用回溯算法解决剑指 Offer 38 题目,即找出字符串的所有排列。通过建立决策树并遍历,避免重复,利用 set 存储唯一结果,最终返回排列数组。
















 174
174

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








