1、各种变换之间的区别与联系
前面已经推导过几种傅里叶变换,现在将傅里叶变换与拉普拉斯变换、Z变换联系与区别以图示方式来概括表示。
如下所示

1.1 傅里叶变换FT到离散傅里叶变换DTFT
现附上FT变换公式(公式中ω是物理频率Ω)

DTFT即在FT基础上时间离散,t->nTs,ΩTs=ω,对t求积分变为对n序列求和。
DTFT需要满足绝对可和的条件,Σ|x[n]|<∞。DTFT变换如下

从CT到DTFT变换频谱变化如下

此处注意Ω和ω的含义与区别。下面介绍几个频率概念。
模拟频率f:每秒经历多少个周期,单位Hz,即1/s;
模拟角频率Ω:每秒经历多少弧度,单位rad/s;
数字频率ω:每个采样点间隔之间的弧度,单位rad。
数字频率与模拟频率相互转化:ω=2*π*f/fs。
通常所说的频率,在没有特别指明的情况下,指的是模拟频率f,其单位为赫兹(Hz),或者为1/秒(1/s),数学
符号用f来表示。这是因为现实世界中的信号大多为模拟信号,频率是其重要的物理特性。以赫兹表示的模拟频
率表示的是每秒时间内信号变化的周期数。如果用单位圆表示的话,如图所示,旋转一圈表示信号变化一个周
期,则模拟频率则指的是每秒时间内信号旋转的圈数。

模拟角频率,数学符号常用Ω来表示,其单位为弧度/秒(rad/s)。从单位圆的角度看,模拟频率是每秒时间内信号旋
转的圈数,每一圈的角度变化为2pi的弧度。
数字频率更准确的叫法应该是归一化数字角频率,其单位为弧度(rad),物理意义是相邻两个采样点之间所变化的
弧度数,数学符号常用ω表示,ω=2pi*f/fs(rad) ,fs为采样频率
模拟频率通过采样后变为数字频率。
例如:
模拟频率f: cos(2π*f*t)
模拟角频率Ω: cos(Ω*t);
对模拟信号进行抽样后t=n*Ts,其中Ts为抽样周期,Ts=1/fs,fs为抽样频率。 把t=n*Ts回带入式子中,这时cos(Ωt)就变成了cos(Ω*Ts*n),此时的角频率称为数字角频率ω,ω=Ω*Ts,即
数字频率ω:cos(Ω*Ts*n)=cos(ωn) [Ts为采样间隔时间]。
关系:
Ω=2π*f;ω =Ω*Ts。
因此上图中信号的DTFT,即采样后信号周期Ts对应数字角频率为ω=Ω*Ts=2π/Ts*Ts=2π。也就是说单位圆中的2π
对应采样频率。
1.2离散傅里叶变换到Z变换
我们从离散时间傅里叶变换DTFT开始讲述Z变换的区别与联系。
DTFT需要满足绝对可和的条件,Σ|x[n]|<∞。但是如果不满足绝对可和的条件,则乘一个指数函数a^(-n),
a为(满足收敛域的)任意实数,则x[n]*a^(-n)的DTFT为

a·e^(jω)是一个极坐标形式的复数,我们把这个复数定义为离散信号的复频率,记为Z,则Z变换公式为
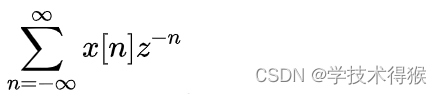
当a=e^(α)时,此时Z=a·e^(jω)=e^(α+jω)
当a=1时,此时Z=a·e^(jω)=e^(jω)即为DTFT变换。 与DTFT建立关系
Z变换解决了不满足绝对可和条件的离散信号,变换到频率域的问题,同时也同样对“频率”的定义进行了扩充。
DTFT的Z变换模值往往都是1, 同样一般在工程应用时,Z变换模值往往也都是1,在单位圆中进行分析。因此,
Z变换与离散时间傅里叶变换(DTFT)的关系是:当z的模为1时,x[n]的Z变换即为x[n]的DTFT。
1.2.1 DTFT的Z变换

DTFT的变换公式,此时Z=e^(jω)可知,e^(jω)是一个单位圆,因此DTFT就是频域转换成一个单位圆,且根据模
拟频率与数字频率的转换关系,2π对应采样周期。n表示信号在频域以不同倍数的采样频率进行周期延拓,通俗来
说就是有n个单位圆。DTFT的Z变换应为一个螺旋的周而复始的一个单位圆。类似一个弹簧。如下所示






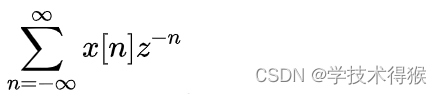









 本文详细探讨了傅里叶变换、拉普拉斯变换与Z变换之间的区别与联系,从FT到DTFT,再到Z变换,以及FT到拉普拉斯变换和拉普拉斯变换到Z变换的过程。重点介绍了脉冲响应不变法和双线性变换法在s域到z域转换中的应用,并分析了Z变换在系统稳定性和幅频特性上的工程应用。
本文详细探讨了傅里叶变换、拉普拉斯变换与Z变换之间的区别与联系,从FT到DTFT,再到Z变换,以及FT到拉普拉斯变换和拉普拉斯变换到Z变换的过程。重点介绍了脉冲响应不变法和双线性变换法在s域到z域转换中的应用,并分析了Z变换在系统稳定性和幅频特性上的工程应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










