正则化（岭回归、lasso回归）、归一化、标准化、离散化、白化、权重、学习率

最新推荐文章于 2024-07-17 00:14:30 发布

遨游的菜鸡

最新推荐文章于 2024-07-17 00:14:30 发布

阅读量1k

点赞数

分类专栏：深度学习文章标签：机器学习

本文链接：https://blog.youkuaiyun.com/qq_34405401/article/details/119578189

版权

深度学习专栏收录该内容

7 篇文章

订阅专栏

本文深入探讨了正则化技术，包括L1（Lasso回归）和L2（岭回归）如何影响模型的过拟合，以及它们在参数稀疏性和大小上的区别。权重衰减和学习率衰减也被讨论，解释了它们在优化过程中的作用。L1正则化倾向于产生稀疏权重矩阵，而L2正则化使参数小以避免过拟合。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

正则化、归一化、标准化、离散化、白化

https://www.bilibili.com/read/cv10712991

1.介绍

正则化的本质可以定义为我们对训练算法所做的任何改变，以减少泛化误差，而不是训练误差。有许多正则化策略。有的对模型进行了额外的约束，如对参数值进行约束;有的对目标函数进行了额外的约束，可以认为是对参数值进行了间接约束或软约束。如果我们小心地使用这些技术，就可以提高测试集的性能。
在实践中使用的主要正则化技术有:
L1 Regularization
L2 Regularization
Data Augmentation
Dropout
Early Stopping
(Online)Label Smooth
在这篇文章中我们首先关注L1正则化、L2正则化、以及易和L2正则化搞混的权重衰减、以及易和权重衰减搞混的学习率衰减。

2.lasso回归（L1）、岭回归（L2）、ElasticNet回归

正则化(Regularization) 是机器学习中对原始损失函数引入额外信息，以便防止过拟合和提高模型泛化性能的一类方法的统称。也就是目标函数变成了原始损失函数+额外项，常用的额外项一般有两种，称作L1正则化和L2正则化，或者L1范数和L2范数（实际是L2范数的平方）。
L1是模型各个参数的绝对值之和；
L1会趋向于产生少量的特征，而其他的特征都是0，产生稀疏权重矩阵；
稀疏性：稀疏性，说白了就是模型的很多参数是0。通常机器学习中特征数量很多，例如文本处理时，如果将一个词组（term）作为一个特征，那么特征数量会达到上万个（bigram）。在预测或分类时，那么多特征显然难以选择，但是如果代入这些特征得到的模型是一个稀疏模型，很多参数是0，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，即使去掉对模型也没有什么影响，此时我们就可以只关注系数是非零值的特征。这相当于对模型进行了一次特征选择，只留下一些比较重要的特征，提高模型的泛化能力，降低过拟合的可能。

L1(lasso回归)：
$L 1$ 正则化与 $L 2$ 正则化的区别在于惩罚项的不同:
$\operatorname{loss} =\min \left(\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{i}\right)-y^{i}\right)^{2}+\lambda \sum_{j=1}^{n}|\theta|\right]\right)$
$L 1$ 正则化表现的是 $\theta$ 的绝对值, 假设模型就只有 $w_{1}$ 和 $w_{2}$ 两个参数， $J_{0}$ 为原始的损失函数，那么化简后可以表示为：
$J=J_{0}+\lambda\left(\left|w_{1}\right|+\left|w_{2}\right|\right)$
那么求最小化 $J_0$ 的过程可以画出等值线，同时 $L_1$ 正则化的函数在二维平面上是菱形，最后在图上表示如下：
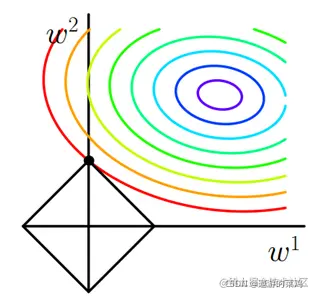
在这里插入图片描述
惩罚项 $L_1$ 表示为图中的黑色棱形，随着梯度下降法的不断逼近，与棱形第一次产生交点，而这个交点很容易出现在坐标轴上。这就说明了L1正则化容易得到稀疏矩阵。

使用场景：
正则化(Lasso回归)可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0，从而增强模型的泛化能力。对于高纬的特征数据,尤其是线性关系是稀疏的，就采用正则化(Lasso回归),或者是要在一堆特征里面找出主要的特征，那么正则化(Lasso回归)更是首选了。

L2是模型各个参数的平方和的开方值。
L2会选择更多的特征，这些特征都会接近于0，当最小化||w||时，就会使每一项趋近于0，防止过拟合。
拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是抗扰动能力强。

简化L2正则化的方程:
$J=J_{0}+\lambda \sum_{w} w^{2}$
$J_{0}$ 表示原始的损失函数, 咱们假设正则化项为: $L=\lambda\left(w_{1}^{2}+w_{2}^{2}\right)$
我们已知圆形的方程: $x-a)^{2}+(y-b)^{2}=r^{2}$
其中 $(a, b)$ 为圆心坐标， $r$ 为半径。那么经过坐标原点的单位元可以写成: $x^{2}+y^{2}=1$ ，正和 $L 2$ 正则化项一样。同时, 机器学习的任务就是要通过一些方法 (比如梯度下降) 求出损失函数的最小值。
此时我们的任务变成在 $L$ 约束下求出 $J_{0}$ 取最小值的解。
求解 $J_0$ 的过程可以画出等值线。同时 $L 2$ 正则化的函数 $L$ 也可以在 $w_1和w_2$ 的二维平面上画出，如下图:
在这里插入图片描述
L表示为图中的黑色圆形，随着梯度下降法的不断逼近，与圆第一次产生交点，而这个交点很难出现在坐标轴上。

这就说明了L2正则化不容易得到稀疏矩阵，同时为了求出损失函数的最小值，使得w1*和w2无限接近于0，达到防止过拟合的问题。
使用场景：
只要数据线性相关，用LinearRegression拟合的不是很好，需要正则化，并且数据并不是线性稀疏时，可以考虑使用岭回归(L2)。

ElasticNet回归:
ElasticNet综合了L1正则化项和L2正则化项，以下是它的公式:

$\min \left(\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{i}\right)-y^{i}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]+\lambda \sum_{j=1}^{n}|\theta|\right)$

ElasticNet回归的使用场景：
ElasticNet在我们发现用Lasso回归太过(太多特征被稀疏为0),而岭回归也正则化的不够(回归系数衰减太慢)的时候，可以考虑使用ElasticNet回归来综合，得到比较好的结果。

2.1 为什么参数稀疏一定程度上会避免过拟合？（L1）

因为参数的稀疏，在一定程度上实现了特征的选择。一般而言，大部分特征对模型是没有贡献的。这些没有用的特征虽然可以减少训练集上的误差，但是对测试集的样本，反而会产生干扰。稀疏参数的引入，可以将那些无用的特征的权重置为0.

2.2 为什么参数越小代表模型越可避免过拟合？（L2）

越是复杂的模型，越是尝试对所有样本进行拟合，包括异常点。这就会造成在较小的区间中产生较大的波动，这个较大的波动也会反映在这个区间的导数比较大。
只有越大的参数才可能产生较大的导数。因此参数越小，模型就越简单。

2.3 L1使参数稀疏、L2使参数小的原因？

L1会使矩阵稀疏以及L2会使参数值偏小的原因：https://blog.youkuaiyun.com/jinping_shi/article/details/52433975；
https://www.cnblogs.com/zingp/p/10375691.html
https://www.huaweicloud.com/articles/e7cd628c86b1ba0a80b87b632432626f.html

3 权重衰减与L2的区别

首先权重衰减和L2并不能画等号，权重衰减只是一种思路，L2是一种具体方法，但是L2可以实现权重衰减，因此L2也常常被用来做权重衰减。

3.1 首先看下权重衰减是什么?

L2正则化是在目标函数中直接加上一个正则项，直接修改了我们的优化目标。
权值衰减是在训练的每一步结束的时候，对网络中的参数值直接裁剪一定的比例，优化目标的式子是不变的。比如每次对权重固定乘以0.8。
在使用朴素的梯度下降法（SGD）时二者是同一个东西，因为此时L2正则化的正则项对梯度的影响就是每次使得权值衰减一定的比例。
但是在使用一些其他优化方法（基于自适应梯度）的时候，就不一样了。比如说使用Adam方法时，每个参数的学习率会随着时间变化。这时如果使用L2正则化，正则项的效果也会随之变化；而如果使用权值衰减，那就与当前的学习率无关了，每次衰减的比例是固定的。因此，L2正则化导致具有较大权值参数或梯度振幅的权重被L2正则化的程度小于使用权重衰减时的情况；而权重衰减因为是按固定比例缩小，因此无论是在SGD还是梯度自适应算法下，权重衰减的程度都是一样的。并且，由于Adam是自适应梯度算法，因此Adam带了L2正则化反而可能导致效果不佳；除此之外，由于具有动量的SGD在深度学习库中实现了L2正则化，因此在对L2正则化有益的任务中，带有动量的SGD反而要比Adam表现要好。
https://www.zhihu.com/question/268068952/answer/536344621
https://cloud.tencent.com/developer/news/631893

3.2 然后L2为什么可以实现权重衰减？

https://blog.youkuaiyun.com/program_developer/article/details/80867468

在这里插入图片描述

4. 学习率衰减

https://blog.youkuaiyun.com/program_developer/article/details/80867468
https://www.huaweicloud.com/articles/f27e2440aac07aaf3acc9d9c72606422.html
在训练模型的时候，通常会遇到这种情况：我们平衡模型的训练速度和损失（loss）后选择了相对合适的学习率（learning rate），但是训练集的损失下降到一定的程度后就不在下降了，比如training loss一直在0.7和0.9之间来回震荡，不能进一步下降。如下图所示：

在这里插入图片描述
遇到这种情况通常可以通过适当降低学习率（learning rate）来实现。但是，降低学习率又会延长训练所需的时间。
学习率衰减（learning rate decay）就是一种可以平衡这两者之间矛盾的解决方案。学习率衰减的基本思想是：学习率随着训练的进行逐渐衰减。
学习率衰减基本有两种实现方法：
线性衰减。例如：每过5个epochs学习率减半。
指数衰减。例如：随着迭代轮数的增加学习率自动发生衰减，每过5个epochs将学习率乘以0.9998。
其他衰减算法在公众号中。
Pytorch学习率衰减介绍：https://zhuanlan.zhihu.com/p/69411064