点击上方“3DCVer”,选择“星标”
干货第一时间送达
本文由知乎作者lowkeyway授权转载,不得擅自二次转载。
原文链接:https://zhuanlan.zhihu.com/p/90122194
在特征点检测的路上,注定要越走越远。但也渐渐触及到了传统CV的核心,如果之前看到好多内容都是星星点点,那么最近的内容就是组合这些散落的繁星,真正落实成能够解决实际问题的美丽图案。
为什么要引入SIFT?
明确目的
不管是Harris还是Shi-Tomas,角点检测检测即便做得再优化,也总是有不可克服的缺点:
对尺度很敏感,不具有尺度不变性
需要设计角点匹配算法
咱们虽然从Harris一路过来,但是要理解这两个缺点,还是有有一些潜在的共识。不管是Harris还是SIFT,再复杂的算法在理解之前一定要不断提醒自己目的是什么?
目的是寻找图像中的特征点!
所有的算法中做的努力都是为了更好的实践这一目标。
什么是特征点?
那么问题是,什么是特征点呢?简单的说就是你感兴趣的点。从人的视角逻辑:比如我们怎么识别人跟人的区别?眼睛、鼻子、嘴巴就是良好的特征点;我们如何识别良品和次品?物体的轮廓就是良好的特征点;在传统CV中,就是要让计算机用它们自己的方式模拟识别宏观上的特征点。
如果让计算机来做人脸识别,来做良品检测,那么首要的就是要让计算机找到对应的特征点,而且是显著的具有良好特性的特征点。什么良好特性呢?比如局部不变性:
尺度不变性:人类在识别一个物体时,不管这个物体或远或近,都能对它进行正确的辨认,这就是所谓的尺度不变性。

旋转不变性:当这个物体发生旋转时,我们照样可以正确地辨认它,这就是所谓的旋转不变性。

再识Harris
我们用这两个“良好”去检验Harris,很容易得到Harris不具备尺度不变性(空间缩放后角点数量、相对位置会变化),但是具备旋转不变性(旋转后的角点还是角点,但是要识别两张旋转图像之间的关系,需要独立设定角点匹配算法)。
从原理上讲就是图片缩放前后的相关矩阵不相似,导致求解特征点会不同。
(如果有读者是算法专家,可以帮忙写一篇数学推导,下面是我搜到的一篇文章)
https://blog.youkuaiyun.com/kxuehen/article/details/40313669
拯救尺度不变性
好了,有问题就会有人解决。
1999年Lowe提出了SIFT(Scale-invariant feature transform,尺度不变性特征变换)特征检测算法,并于2004年对其完善总结。其应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对。
在没有诞生深度神经网络的image net比赛中,SIFT一直都是霸榜的存在。在特征点检测的传统CV算法中,SIFT也是No1的引用。
需要注意的是:此算法有其专利,专利拥有者为英属哥伦比亚大学。
SIFT确立的特征点不会因为视角的改变(尺度变化和旋转变化)、光照的变化(亮度变化)、噪音的干扰(噪声干扰)而消失,比如角点、边缘点、暗区域的亮点以及亮区域的暗点。这样如果两幅图像中有相同的景物,那么这些稳定点就会在两幅图像的相同景物上同时出现,这样就能实现匹配。
迫不及待了,SIFT怎么做到的?
SIFT的实现
先提醒自己,我们的目的是什么?寻找图像中的特征点,良好特征点!
实现SIFT,可以分成如下几个步骤。
构建高斯多尺度金字塔
为了解决尺度敏感问题,最正常的思路就是在多尺度下做运算。然后,要解决多尺度问题,首先就要搞清楚什么是尺度空间?以及单尺度下该怎么构建?
1、首先,要做的是要创建一个尺度空间。
单尺度空间在宏观上可以理解成在相同位置观察到的世界,至于你有没有带眼睛无所谓;从数字图像微观理解就是在相同分辨率下的图片,至于你有没有做锐化、没有有做模糊无所谓。
多尺度空间在宏观上可以理解成在不同位置观察到的世界,当然也同是否带眼睛无关;从数字图像微观理解就是在不同分辨率下看相同的图片,当然也与锐化、模糊无关。
有这个理解就够了。Lowe告诉我们,在单尺度空间下要有6张图片。(为什么是6张的建议值,这里先Mark一下,后面会提到),就像下图:
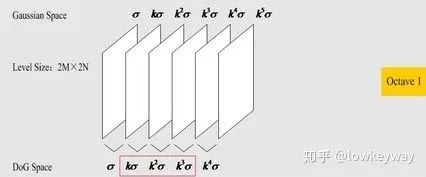
这六张图从左到右,分别是原图(论文中的第一层实际上是把原图的分辨率提高了4倍 2M*2N)经过方差为 、
、
、
、
、
的高斯滤波后的图片,即从左到右图片应该越来越模糊。
算法规定(第一层):
的取值为1.6
的取值为
(
,S表示需要得到多少个高斯金字塔层数,这里是3)
如果要用公式精确表示这里的一张图:
其中
是二维高斯模糊的算子。
是原图
表示卷积,即做了高斯模糊
表示处理后的照片
2、然后,做这一层的DoG
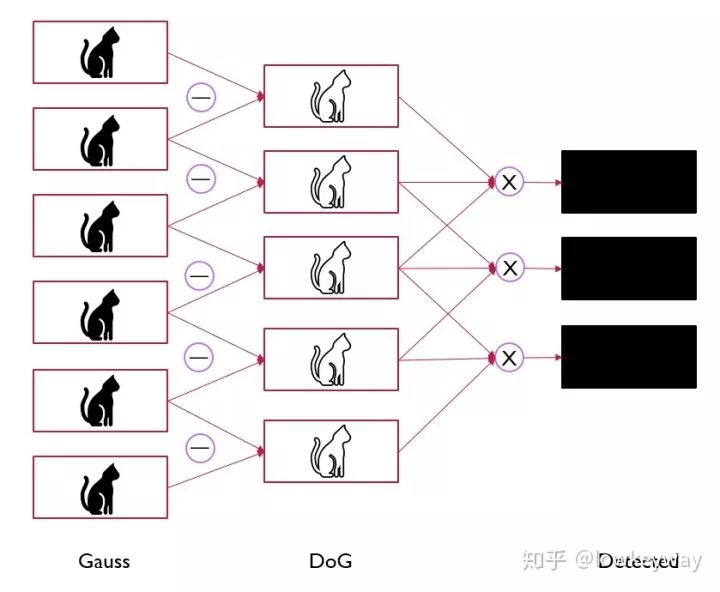
高斯模糊咱们之前有聊过(而且不止一次),问题是,我们的现在要做的是特征值检测,做不同程度的高斯模糊有什么用呢?

看,不同期望的高斯模糊后的图片差值,是不是就有了一个物体的轮廓?轮廓是什么?哈哈,最原始的特征出现了!!!
用数学公式表示:
它就形象的被称为difference of gaussian(DOG)
我们知道,一个空间尺度上有6张图片。每相邻的两张图片之差就会产生一张DoG, 所以总共可以产生5幅DoG:
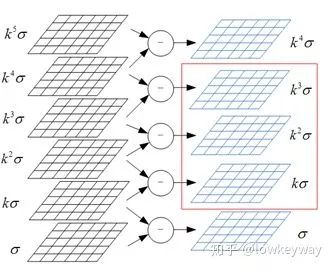
3、最后, 构建金字塔空间
如果说我们构造不同高斯模糊图片是为了获得带有特征值的DoG图片,那么下一步就该不忘初心,想一想怎么解决尺度不变性。
Binggo!对,就是拿金字塔把特征值拓展到多分辨率上。
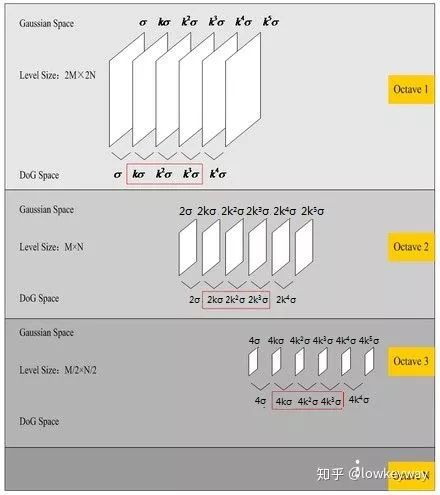
相同分辨率的照片组成一个尺度空间,每个尺度空间由6张递增高斯模糊处理的照片构成;
根据金字塔原理,把尺度空间拓展到3个,称为高斯金字塔的组数。
这里需要解释几个名词和关键变量:
高斯金字塔的组数(Octave):即尺度空间的个数。
S(Scale?):表示一个尺度空间(也就是金字塔的一组)挑选出来做特征值搜索的图片个数(也即层数)。
系数
高斯模糊的期望序列
,
表示是高斯金字塔的第几组。
多尺度空间构建好后,就可以得到DoG的多尺度空间:
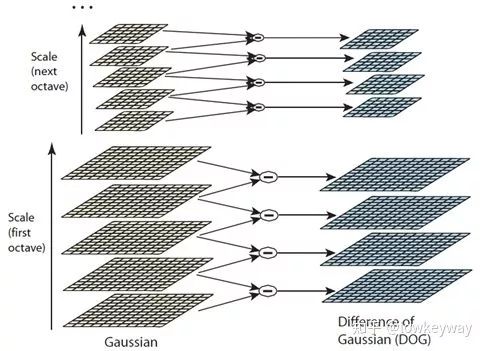
番外篇:这些图片有没有让你想起了想起了拉普拉斯金字塔?
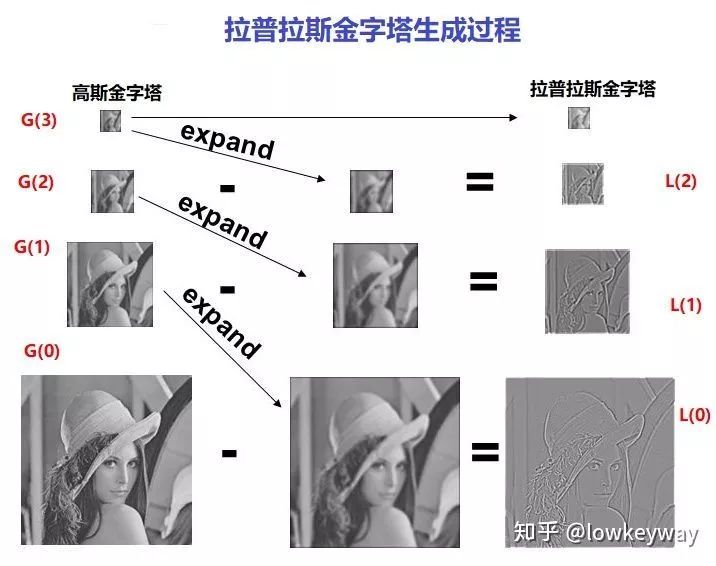
检测尺度空间的极值点
我们拿到了一组多空间下的带有特征值Dog金字塔,但是轮廓信息并不是我们的最终目的,我们想要的是特征点,那下一步怎么办呢?Lowe说由轮廓的线变成点,那就找极值点吧。
1、 首先,我们要找到金字塔中一组的极值点。
怎么找呢?暴力解决!一幅DoG图像,从左到右,从上到下依次轮询每个点,让目标点跟它周围的8邻域的8个点比较,除此之外,我们每一层不是还生成了5幅DoG图像吗?同时也让目标点跟它相邻Scale的DoG图像做三维的空间比较。
如下图,这样一个目标点就会同周边26个点比较。
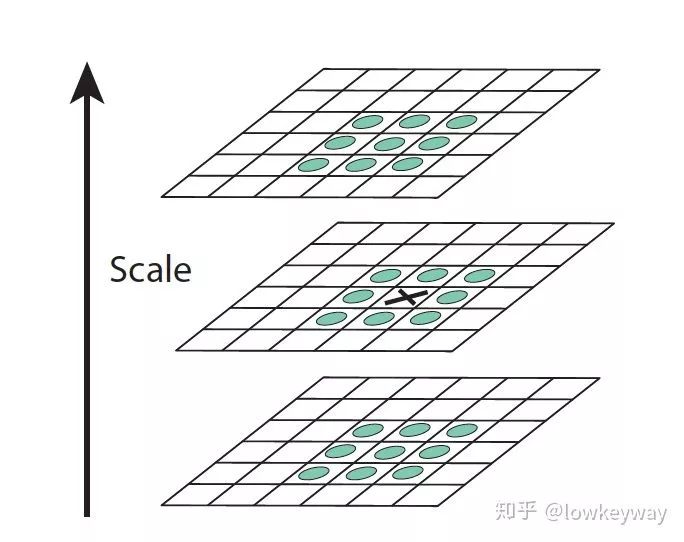
如果一个点经过如此比较后,确实是这26个点中的极大或极小值,就认为该点是图像在该尺寸下的极值点。
可以想象,如果一个空间有6张图,那么产生5张DoG,到这里就只有3张可供选择的特征点了(以内顶层和底层无法凑够26个点),这也是S=3的由来!
2、然后,把它拓展到多尺度空间
其实,拓展这件事情很好做,只要在不同的尺度空间(金字塔的不同组)做一遍相同的事情就OK了,这也是保证多尺度不变性的关键。
但是,有一个隐藏的坑:怎么保证最终得到的特征点满足尺度空间的连续性?
答案就在构建金字塔的时候一个尺度空间并不是拿原图直接做分辨率缩放,然后再依次做高斯模糊的,而是取上一张的倒数第3张图像隔行采样后作为下一组的第一张图像!
我们从逻辑上想:
6张图片要减去倒数第一张变成了5张DoG,5张DoG里面倒数第一张又不能参与特征值的提取,是不是本尺度空间的关键信息点都是倒数第三张?如果为了保证下一个尺度空间的特征值连续,是不是应该以该图作为基准点做缩放?
从公式上推导:
我们知道对于尺度空间第o组,第s层的图像,它的尺度为 ,其中,
,那么我们从第0组开始,看它各层的尺度。
第0组:
第1组:
我们只分析2组便可以看出,第1组的第0层图像恰好与第0组的倒数第三幅图像一致,尺度都为 ,所以我们不需要再根据原图来重新卷积生成每组的第0张图像,只需采用上一层的倒数第3张来降采样即可。
另一个角度考虑,如果我们把它们的中间三项取出来拼在一起,则尺度为: 正好连续!!这一效果带来的直接的好处是在尺度空间的极值点确定过程中,我们不会漏掉任何一个尺度上的极值点,而是能够综合考虑量化的尺度因子。
做完这两个步骤后,应该就可以在原图上画出来极值点坐标了示意图了:
精确定位极值点
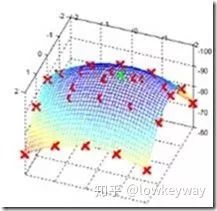
嗯,不错。极值点检索完毕后是不是大功告成了?Lowe说还不够完美。原因是我们求得的极值点的搜索是在离散空间中进行的,检测到的极值点并不是真正意义上的极值点。比如上图中红色的叉标记图像中的像素,但是真正的极值点是绿色的位于像素间的点
1、 首先,我们要明确为什么要对定位后的极值点再做精确定位。
下图显示了一维信号离散空间得到的极值点与连续空间的极值点之间的差别。利用已知的离散空间点插值到连续空间极值点的方法叫子像元插值。
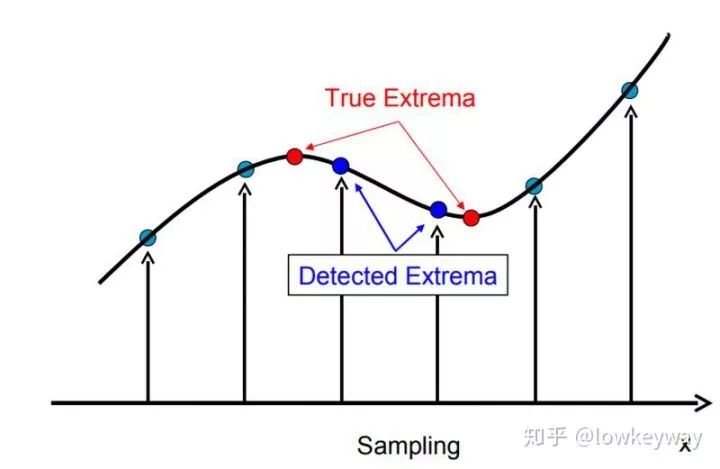
2、 其次,再探讨一下如何精确。
利用已知的离散空间点插值得到的连续空间极值点的方法叫做子像素插值(Sub-pixel Interpolation)为了提高关键点的稳定性,需要对尺度空间DoG函数进行曲线拟合。利用DoG函数在尺度空间的Taylor展开式(拟合函数)为:
其中 ,求导并让方程等于零,可以得到极值点的偏移量为:
通过对x求偏导并将结果置为零,我们可以简单地计算出方程的极值,从而得到子像素特征点的位置,这些子像素点可以增加匹配和算法稳定性的机率。
若子像素点与近似特征点间的偏移量大于0.5,则按照偏移近似特征点的方向相应改变(移动)特征点,然后再把该点当做近似特征点,重复该操作((Lowe算法里最多迭代5次),直到子像素点与近似特征点间的偏移量小于等于0.5。
得到最终候选点的精确位置与尺度 ,将其代入公式求得
,求其绝对值得
。如果其绝对值低于阈值的将被删除。
3、 删除边缘效应
为了得到稳定的特征点,只是删除DoG响应值低的点是不够的。由于DoG对图像中的边缘有比较强的响应值,而一旦特征点落在图像的边缘上,这些点就是不稳定的点。一方面图像边缘上的点是很难定位的,具有定位歧义性;另一方面这样的点很容易受到噪声的干扰而变得不稳定。
一个平坦的DoG响应峰值往往在横跨边缘的地方有较大的主曲率,而在垂直边缘的方向有较小的主曲率。而主曲率可以通过2×2的Hessian矩阵H求出:
上式中, 值可以通过求取邻近点像素的差分得到。
的特征值与
的主曲率成正比例。我们可以避免求取具体的特征值,因为我们只关心特征值的比例。令
为最大的特征值,
为最小的特征值,那么,我们通过
矩阵直迹计算它们的和,通过
矩阵的行列式计算它们的乘积:
如果 为最大特征值与最小特征值之间的比例,那么
,这样便有
上式的结果只与两个特征值的比例有关,而与具体特征值无关。当两个特征值相等时, 的值最小,随着
的增加,
的值也增加。所以要想检查主曲率的比例小于某一阈值
,只要检查下式是否成立:
Lowe在论文中给出的 。也就是说对于主曲率比值大于10的特征点将被删除。
这一堆东西真是晦涩,不过他的物理所用就是滤除大部分边缘,去找真正的关键信息。
角点?不全是,角点关注的是两个特征值的大小,这里关注的是两个特征值的比值。主要是去除DoG局部曲率非常不对称的像素。
选取特征点方向
好了,到这一步,我们已经完成了特征点的筛选,并且通过高斯金字塔的设计实现了尺度不变性。接下来,就该去搞定旋转不变性了。
这里的旋转不变性跟咱们角点自带的旋转不变性有一些不同。Harris的角点不变性靠的是旋转后,该是角点的地方还是角点,所以对于整张图对应的所有角点这个尺度看,它是具备旋转不变性的。但是SIFT中,我们希望给每个特征点赋值一个方向,这样,对于单个特征点来说,不管是如何缩放、旋转,这个方向作为它的一个属性都不会变。
了解了我们的目的,下一步就是要实现它,给每个特征点附加一个方向属性。
1、 首先,要明确什么是特征点的方向?
还记得Harris怎么判断角点、边缘、团点的吗?对,对某一方向求偏导。同理,特征店的方向也可以通过选取特征点周边图像,求梯度方向和大小。
求得的最显著的梯度大小付给该特征点,就称为了该特征点的方向!
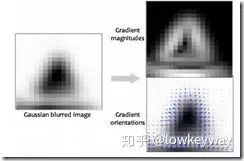
2、 然后,想办法求特征点的方向。
采集其所在高斯金字塔图像3σ邻域窗口内像素的梯度和方向分布特征。梯度的模值和方向如下:
L为关键点所在的尺度空间值,按Lowe的建议,梯度的模值m(x,y)按 的高斯分布加成,按尺度采样的3σ原则,邻域窗口半径为
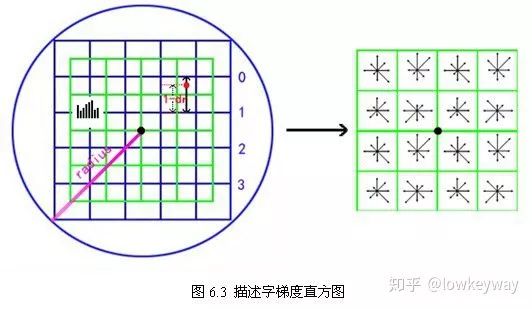
在完成关键点的梯度计算后,使用直方图统计邻域内像素的梯度和方向。梯度直方图将0~360度的方向范围分为36个柱(bins),其中每柱10度。如图所示,直方图的峰值方向代表了关键点的主方向,(为简化,图中只画了八个方向的直方图)。
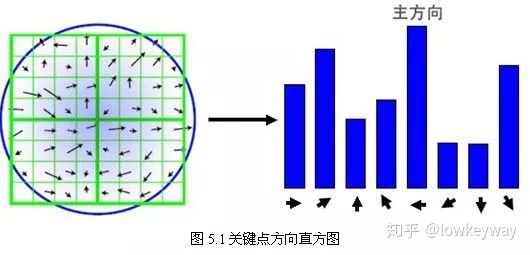
直方图的峰值则代表了该关键点处邻域梯度的主方向,即作为该关键点的方向;其他的达到最大值80%的方向可作为辅助方向。
为了增强匹配的鲁棒性,只保留峰值大于主方向峰值80%的方向作为该关键点的辅方向。因此,对于同一梯度值的多个峰值的关键点位置,在相同位置和尺度将会有多个关键点被创建但方向不同。仅有15%的关键点被赋予多个方向,但可以明显的提高关键点匹配的稳定性。实际编程实现中,就是把该关键点复制成多份关键点,并将方向值分别赋给这些复制后的关键点,并且,离散的梯度方向直方图要进行插值拟合处理,来求得更精确的方向角度值,
至此,将检测出的含有位置、尺度和方向的关键点即是该图像的SIFT特征点。
生成关键点描述子
完美...了吗?
金字塔保证特征点的空间不变性, 严格删选保证了特征点的准确性, 方向信息保证了特征点的旋转不变性。我们如何把所有信息作为属性附加给关键点呢?
1、 首先,要了解为什么要给关键点增加描述子
通过上面的步骤,对于每一个关键点,拥有三个信息:位置、尺度以及方向。接下来就是为每个关键点建立一个描述符,用一组向量将这个关键点描述出来,使其不随各种变化而改变,比如光照变化、视角变化等等。这个描述子不但包括关键点,也包含关键点周围对其有贡献的像素点,并且描述符应该有较高的独特性,以便于提高特征点正确匹配的概率。
2、 然后,考虑如何增加
SIFT描述子是关键点邻域高斯图像梯度统计结果的一种表示。通过对关键点周围图像区域分块,计算块内梯度直方图,生成具有独特性的向量,这个向量是该区域图像信息的一种抽象,具有唯一性。
表示步骤如下:
1) 确定计算描述子所需的图像区域
特征描述子与特征点所在的尺度有关,因此,对梯度的求取应在特征点对应的高斯图像上进行。将关键点附近的邻域划分为d*d(Lowe建议d=4)个子区域,每个子区域做为一个种子点,每个种子点有8个方向。每个子区域的大小与关键点方向分配时相同。
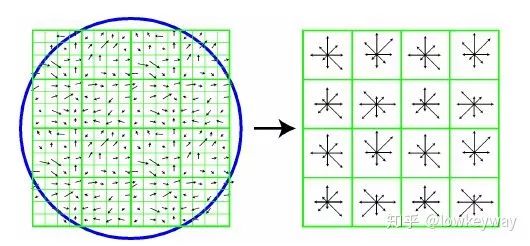
每一个小格都代表了特征点邻域所在的尺度空间的一个像素 ,箭头方向代表了像素梯度方向,箭头长度代表该像素的幅值。然后在4×4的窗口内计算8个方向的梯度方向直方图。绘制每个梯度方向的累加可形成一个种子点。
2) 将坐标轴旋转为关键点的方向,以确保旋转不变性
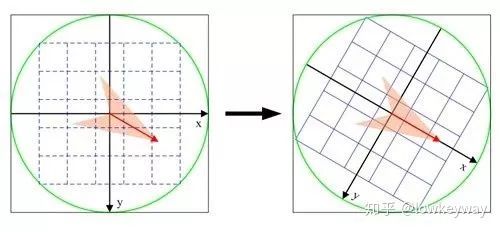
3) 将邻域内的采样点分配到对应的子区域内,将子区域内的梯度值分配到8个方向上,计算其权值
其中a,b为关键点在高斯金字塔图像中的位置坐标。
4) 插值计算每个种子点八个方向的梯度
5) 归一化
如上统计的4*4*8=128个梯度信息即为该关键点的特征向量。特征向量形成后,为了去除光照变化的影响,需要对它们进行归一化处理,对于图像灰度值整体漂移,图像各点的梯度是邻域像素相减得到,所以也能去除。
6) 向量门限
描述子向量门限。非线性光照,相机饱和度变化对造成某些方向的梯度值过大,而对方向的影响微弱。因此设置门限值(向量归一化后,一般取0.2)截断较大的梯度值。然后,再进行一次归一化处理,提高特征的鉴别性。
7) 排序
按特征点的尺度对特征描述向量进行排序。
这群科学家,真让人头大。对于工程狗,其实就一张图:
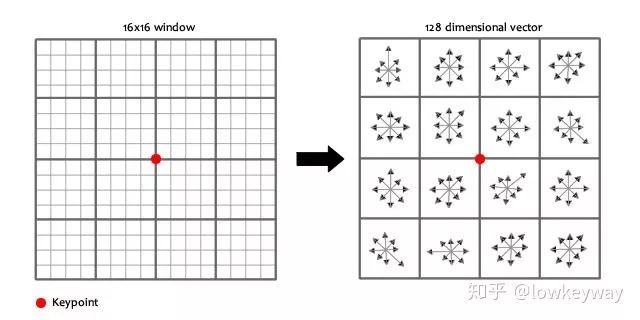
在每个4*4的1/16象限中,通过加权梯度值加到直方图8个方向区间中的一个,计算出一个梯度方向直方图。这样就可以对每个feature形成一个4*4*8=128维的描述子,每一维都可以表示4*4个格子中一个的scale/orientation. 将这个向量归一化之后,就进一步去除了光照的影响。
SIFT有什么用?
我们了解过如何用SIFT生成特征点,有了这些特征点后,我们就可以做匹配了!
如何匹配?
1、 首先还是要对图片生成特征点
一张图经过SIFT算法后,会得到多个特征点,每个特征点有128维的描述子属性。那么,匹配特征点都简单多啦!
生成了A、B两幅图的描述子,(分别是k1*128维和k2*128维),就将两图中各个scale(所有scale)的描述子进行匹配,匹配上128维即可表示两个特征点match上了。
2、 然后考虑怎么匹配
当两幅图像的SIFT特征向量生成后,下一步我们采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。取图像1中的某个关键点,并找出其与图像2中欧式距离最近的前两个关键点,在这两个关键点中,如果最近的距离除以次近的距离少于某个比例阈值,则接受这一对匹配点。降低这个比例阈值,SIFT匹配点数目会减少,但更加稳定。
写代码的时候才想起来,SIFT是在xfeatures2d模块里面的,而我们现在还在用官方编译好的opencv_world410d.dll, 而且还有专利问题没有解决。这些都需要我们自己编译OpenCV的源代码以及三方扩展库。配置自己的环境。做了一篇环境配置的教程,分享一下:
https://zhuanlan.zhihu.com/p/90810839
C++
#include <opencv2/opencv.hpp>
#include <opencv2/xfeatures2d.hpp>
#include <iostream>
using namespace cv;
using namespace cv::xfeatures2d;
using namespace std;
int main(int argc, char** argv) {
Mat cat = imread("cat.png");
Mat smallCat = imread("smallCat.png");
imshow("cat image", cat);
imshow("smallCat image", smallCat);
auto detector = SIFT::create();
vector<KeyPoint> keypoints_cat, keypoints_smallCat;
Mat descriptor_cat, descriptor_smallCat;
detector->detectAndCompute(cat, Mat(), keypoints_cat, descriptor_cat);
detector->detectAndCompute(smallCat, Mat(), keypoints_smallCat, descriptor_smallCat);
Ptr<FlannBasedMatcher> matcher = FlannBasedMatcher::create();
vector<DMatch> matches;
matcher->match(descriptor_cat, descriptor_smallCat, matches);
Mat dst;
drawMatches(cat, keypoints_cat, smallCat, keypoints_smallCat, matches, dst);
imshow("match-demo", dst);
waitKey(0);
return 0;
}


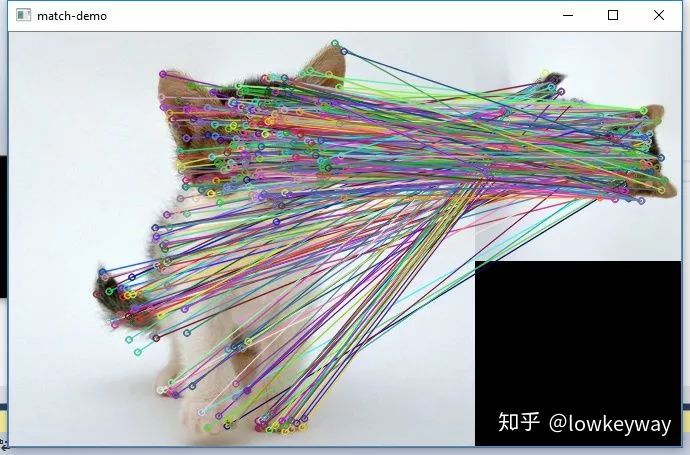
参考:
https://blog.youkuaiyun.com/u010440456/article/details/81483145
https://www.cnblogs.com/ronny/p/4028776.html
本文仅用做学术分享,如有侵犯版权,请联系作者,会自行删文。
重磅!3DCVer-学术交流群已成立
欢迎加入我们公众号读者群一起和同行交流,目前有3D视觉、CV&深度学习、SLAM、三维重建、点云后处理、自动驾驶、CV入门、医疗影像、缺陷检测、行人重识别、目标跟踪、视觉产品落地、视觉竞赛、车牌识别等微信群,请扫描下面微信号加群,备注:”研究方向+学校/公司+昵称“,例如:”3D视觉 + 上海交大 + 静静“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进去相关微信群。原创投稿也请联系。

▲长按加群

▲长按关注我们























 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








