算法学习笔记

学习多是一件美事啊

已于 2023-10-12 15:12:51 修改

阅读量243

点赞数

CC 4.0 BY-SA版权

文章标签：算法学习笔记

于 2023-10-08 16:33:02 首次发布

本文链接：https://blog.youkuaiyun.com/qq_28601023/article/details/133603533

文章目录

前言
一、最小树形图
二、DFS树
三、无向图的割顶
四、强连通分量
五、支配集、独立集、覆盖集
六、最大网络流
总结

前言

记录学习中遇到的难点

一、最小树形图

出自《图论的算法与程序设计》 $P 27$ 步骤 $3$ 只告诉了我们性质没有证明，现做笔记如下：
把环收缩 $C_i$ 收缩成点 $U_i$ 还是很好理解的，但是在收缩后的图中为什么要改变收缩点为终点的边的权值？

记原图为 $D_0$ ，收缩后的图记为 $D_1$ 。

首先如果要构成树形图，那么必然不能有圈，因此我们必然要在圈 $C_i$ 上去掉一条弧，不妨设被去掉的弧叫做 $A_t$ ，而 $A_t$ 原来指向的顶点是 $V_s$ ，此时 $V_s$ 没有前继了，这样 $V_s$ 就不能称为树形图的节点了，因为树形图上除了根 $V_1$ ，其他节点都有前继。

所以我们必须从指向 $U_i$ 的众多弧中选择一条，并且这条弧在展开 $U_i$ 后也要指向 $V_s$ ，不妨设这条弧就是 $A_k$ ，在 $D_1$ 中对这些弧的权值做调整： $L_{D_1}(A_k)=L_{D_0}(A_k)-L_{D_0}(A_t)$ 。那么如果 $D_1$ 中选择 $A_k$ 作为树形图的弧，那么无论是在 $D_1$ 中观察，还是在展开圈 $C_i$ 中观察（展开后要取掉 $A_t$ ），总的权值相同，这一点很重要因为我们可以把 $D_0$ 上的最小树形图问题转化到 $D_1$ 上的最小树形图问题。

如果我们在 $D_1$ 中找到了根节点为 $V_1$ 的最小树形图，那么把 $U_i$ 展开，也就是在 $D$ 中加入 $D_1$ 中选择的最优的 $A_k$ ，然后再 $C_i$ 中去掉对应的 $A_t$ 。就可以得到 $D_0$ 中的最小树形图。
我们从 $D_0$ 破圈成树形图的各种操作来看待上述说法：
1. $D_0$ 中的最小树形图还需要去掉了圈 $C_i$ 中的弧 $A_p$ 再加入指向 $U_i$ 的弧 $A_q$ ，但是 $L_{D_0}(A_q)-L_{D_0}(A_p)\ge0$ ，显然会导致总权值增加。
2.并且由于在 $D_1$ 中我们的算法选择了 $min\{L_{D_1}(A_k)\}$ ，因此 $L_{D_0}(A_k)-L_{D_0}(A_t)\le L_{D_0}(A_q)-L_{D_0}(A_p)$ ，如果不选 $A_k$ 加入而去选 $A_q$ 加入，那么总的权值一定会增加的。
3.我们之加入 $A_k$ 并去掉 $A_t$ ，显然已经能够得到一棵树形图。

第二点书上提到如果 $D_1$ 中没有 $V_1$ 为根的最小树形图，那么 $D_0$ 中也不会有。
如果 $D_1$ 中没有最小树形图只能说明 $V_1$ 不能延某条路径道道某节点，该节点要么是缩点 $U_i$ ，要么是普通节点（ $D_0$ 有的点），无论如何从 $D_0$ 的角度看就是 $V_1$ 到某节点通不了。

这样就理解了算法的原理，主要有三个要点：
1.缩点后在新图上指向 $U_i$ 的弧要进行权值调整
2.如果新图找不到最小树形图则原图也找不到
3.如果新图找到了最小树形图则通过上面的展开步骤可以得到原图的最小树形图

二、DFS树

出自《图论的算法与程序设计》 $4.2$ 节，感觉DFS树的概念非常重要。
图的DFS是仿照树的先序遍历顺序去访问每一条边 $(U, W)$ 的。加入我们已经访问了顶点 $U$ ，现在正在访问 $U$ 的儿子 $W$ 并且 $W$ 以前还未访问过，则 $(U, W)$ 就是树枝。在DFS过程中顶点和树枝构成树，叫做DFS树。

一般为了处理一些问题，我们按照每个顶点第一次访问到的顺序给顶点一个顺序索引叫做： $df n [U]$ 。

图在DFS过程中除了会产生树枝以外还有一些被访问的边是非树枝的边。
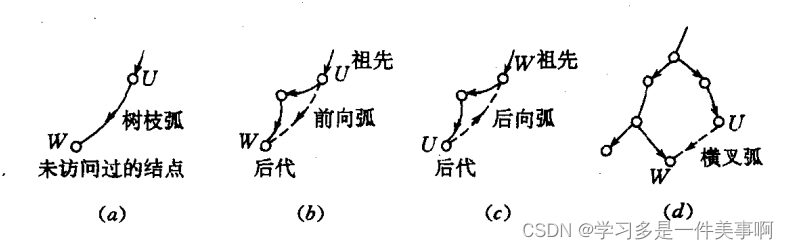
在这里插入图片描述
有向图的DFS过程只能产生四种类型的弧：树枝、前向弧、后向弧、横叉弧。
$(a)$ 如果访问了 $U$ ，紧接着访问了 $U$ 的儿子 $W$ ，并且 $W$ 未被访问过，则 $(U, W)$ 是DFS树的树枝，显然 $df n [W] > df n [U]$ 。
$(b)$ 如果访问了 $U$ ，后来遍历了 $U$ 的一棵子树，并且子树中包含 $W$ （不为根节点），如果在未来的某个时刻从 $U$ 开始找新子树遍历的时候发现了 $U$ 的儿子 $W$ （从图角度看），我们会发现 $W$ 已经被访问多了，此时 $(U, W)$ 不能说是树枝，只能就叫做前向弧，此时也有 $df n [W] > df n [U]$ 。
$(c)$ 如果访问了 $W$ ，后来正在遍历 $W$ 的一棵子树，并且子树中包含 $U$ （不为根节点），在对 $U$ 进行DFS搜索时，发现 $U$ 的一个儿子是 $W$ （从图的角度看），此时 $(U, W)$ 是后向弧，此时 $df n [W] < df n [U]$ 。
$(d)$ 如果已经访问了某顶点，后来先遍历了一棵子树，该子树包含 $W$ （不为根节点），再后来正在遍历令一棵子树，该子树包含 $U$ （不为根节点），在对 $U$ 进行DFS搜索时发现 $U$ 的一个儿子是 $W$ （从图的角度看），则 $U$ 和 $W$ 没有直系亲属关系，弧 $(U, W)$ 被称为横叉弧，此时 $df n [W] < df n [U]$ 。

根据我们DFS先序遍历的顺序， $(d)$ 中的横叉弧只能是从 $U$ 指向 $W$ 的。

并且可以想到如果图是无向图的话是不可能存在横叉弧的情况的。
无向图的DFS过程只能产生三种类型的弧：树枝、前向弧、后向弧。也就是如果无向图中有边 $(U, W)$ ，则 $U$ 和 $W$ ，必有一个是祖先一个是后代，无向图的DFS树中不会产生图 $(d)$ 的情况。

三、无向图的割顶

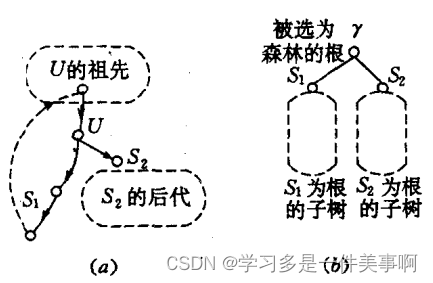
在这里插入图片描述

如果 $U$ 是割顶，则：
1.如果 $U$ 是根节点，则只要它的儿子多于一个就一定是割顶
2.如果 $U$ 不是根节点，则如果它有一棵子树，该子树中没有到 $U$ 的祖先的后向边，那么 $U$ 也是割顶

无向图中判断是不是后向边非常容易，从DFS树可以看出只要 $df n [W] < df n [U]$ 那么 $(U, W)$ 就是后向边。

设函数 $L O W (S)$ 表示在DFS树上，顶点 $S$ 以及 $S$ 的后代通过后向边能够返回的最早的祖先（每个顶点可用 $df n$ 标记），显然在DFS树上要返回祖先只能通过后向边。

从 $(a)$ 可以看到，如果 $U$ 有一个儿子 $S$ 使得 $LOW(S)\ge dfn[U]$ ，那么 $S$ 以及 $S$ 的后代无法返回比 $U$ 更早的祖先，那么 $U$ 就是割顶了。

我们想要在DFS过程中更新个点的 $L O W$ ，它的递归结构如下：
$LOW(U)=\left\{ \begin{align} &&dfn[U]&&第一次访问U,\\ &&min\{LOW(U),dfn[W]\}&&检测到后向边(U,W),\\ &&min\{LOW(U),LOW(S)\}&&U的所有儿子S均处理完之后, \end{align} \right.$
对于顶点 $U$ ，如果在程序执行过程中，一旦某个儿子 $S$ 使得 $LOW(S)\ge dfn[U]$ 就可以判断 $U$ 是割顶，不用等到所有的儿子的 $L O W (S)$ 值都出来。然后接着继续进行DFS，直到对根节点DFS完成之后才停止算法，这样就找出了全部的割顶了。

书上开始用了一个式子： $LOW(U)=min\{dfn[U],LOW[S],dfn[W]\}$ ，我们在完整的DFS树上来理解这件事：

首先 $U$ 是自己的祖先，然后 $U$ 通过儿子们能够回到的最早祖先是 $L O W [S]$ ， $U$ 通过后向边 $(U, W)$ 能够返回的祖先是dfn[W]，在里面找一个 $df n$ 号最小的祖先就是能够返回的最早的祖先了。另外 $df n [U]$ 也是必须的，比如 $U$ 无法通过后两个途径返回祖先，那么只好让 $L O W (U) = df n [U]$ ，总不能乱写吧， $L O W (U)$ 也有可能被其他顶点递归调用呢。

如果想要输出块，则可以这样处理，每个顶点再第一次访问的时候都入栈，如果出现了 $LOW(S)\ge dfn[U]$ ，则 $U$ 是割顶：
1.如果 $U$ 不是根节点，则把儿子 $S$ 以及儿子上面的顶点（其实就是以 $S$ 为根的DFS树中成块的部分）作为块弹出，可以附加上割顶 $U$ 指示是通过哪个割顶分割得到的块。每个儿子都可以这样处理。
2.如果 $U$ 是根节点，则把它的每个儿子 $S$ 以及栈中 $S$ 以上的节点一同依次弹出可以附加上割顶 $U$ 作为指示。

四、强连通分量

每一个强连通分量在DFS树上看都是以最小 $df n$ 开始的节点为根节点 $r_i$ 的树。

该树在这个强连通分量中，因此树上的某个顶点 $U$ 一定能够通过树枝、前向弧、后向弧、横叉弧返回到树根 $r_i$ 上。

假设某强连通分量在DFS树上以 $r_i$ 为根节点，用 $L O W L I N K (U)$ 表示 $U$ 能够在DFS树上返回的 $df n$ 最小顶点的 $df n$ 值。那么如果从 $r_i$ 开始做DFS，DFS返回后必然会发现 $LOWLINK(r_i)=dfn[r_i]$ 。

书上用 $LOWLINK(U)=min\{dfn[U],dfn[W]\}$ ，其中 $W$ 表示在DFS树上从 $U$ 及其后代出发能够返回的 $df n$ 最小的顶点。

其递归定义如下：
$LOWLINK(U)=\left\{ \begin{align} &&dfn[U]&&第一次访问U,\\ &&min\{LOWLINK(U),dfn[W]\}&&检测到当前树中后向弧(U,W),\\ &&min\{LOWLINK(U),dfn[W]\}&&检测到当前树中横叉弧(U,W),\\ &&min\{LOWLINK(U),LOWLINK(S)\}&&U的所有儿子S均处理完之后, \end{align} \right.$
当前树意思是，已经找到的连通分量已经输出，后续正在DFS的个点形成的树。

算法通过弹栈的方式输出强连通分量，这里理解一下：
首先想一下，我们正在对某根节点 $r_i$ 进行DFS，每一个顶点再进行DFS前就进行入栈，如果先前已经对某点 $T$ 进行了DFS，并且返回时发现 $L O W L I N K (T) = df n [T]$ ，则栈中会弹出若干顶点，一致直到 $T$ 弹出为止，其实这些弹出的点就是以 $T$ 为根的连通分量。

所以要保证 $(U, W)$ 到底是在当前正在搜索的树中，只需要看 $W$ 在堆栈中的顶点就可以了。

这里说法可能还有些疑问，归纳假设一下：假设问题的规模小于连通分量 $T$ ，的时候上面的弹栈操作总能给出连通分量，首先当 $T$ 进行完DFS时有 $L O W L I N K (T) = df n [T]$ ，代表 $T$ 经过后代能够返回到 $T$ ，如果 $T$ 的子树中如果有节点不能返回 $T$ 怎么办呢？其实不用担心，假设 $T$ 中还包含不能到达 $T$ 的点，它们必定属于其他的强连通分量，树 $T$ 包含这些强连通分量的生成树，不妨设某连通分量的根为 $T^{'}$ ，那么 $T^{'}$ 的DFS完之后一定有 $L O W L I N K (T ’) = df n [T^{'}]$ ，此时连通分量 $T^{'}$ 的规模小于连通分量 $T$ 的规模，因此弹栈直到 $T^{'}$ 被弹出就等价于输出了强连通分量 $T^{'}$ 。这时候会不会把强连通分量 $T$ 中的顶点带出来了呢？如果是那样那么两连通分量就属于同一连通分量了，和假设矛盾了。因此到 $T$ 的DFS完成之前，就已经把不在强连通分量 $T$ 中的点弹出了，所以到弹 $T$ 的时候弹出的顶点就是强连通分量 $T$ 了。当问题的规模降到一个顶点的时候显然成立，因此做法是正确的。

还有一个问题，在DFS的过程中来找后向弧和横叉弧有没有问题，其实因为这两种弧都要求 $df n [W] < df n [U]$ ，所以访问新的顶点 $U$ 的时候只需要检查先前已经访问过点 $W$ 即可。

五、支配集、独立集、覆盖集

书上 $P 54$ 页只给出了支配集的两个性质：

1.若图 $G$ 中无零次顶点，则存在一个支配集 $D$ ，使得 $G$ 中除去 $D$ 后的其他顶点构成也是支配集。

说明一下这个事情：不妨设图 $G$ 是连通的，那么 $G$ 中存在生成树，祖宗（根节点）涂上黑色，二代目涂上白色，三代目涂上黑色……，则黑色点集合和白色点集合就是两个满足要求的支配集。

2.若图 $G$ 中无零次顶点， $D_1$ 为极小支配集，则 $G$ 中除去 $D_1$ 后其他顶点构成一个支配集。

为了叙述方便我们用 $V (G)$ 表示 $G$ 的顶点集合
证明：假设 $V(G)-D_1$ 不是支配集，那么在 $D_1$ 中至少存在一点 $x$ ，它不和 $V(G)-D_1$ 中的点相连，但是我们注意到这样的 $x$ 必须连接在 $D_1$ 的其他点上的，否则由于它和 $V(G)-D_1$ 是不相连的，那么这个 $x$ 在图 $G$ 上就是孤立的（零次顶点了）。由于 $x$ 连接在 $D_1$ 的其他点上的，显然 $D_1$ 去掉 $x$ 之后还是支配集，因此 $V(G)-D_1$ 必须是支配集。

然后书上莫名其妙地给出了计算所有极小支配集的布尔运算公式：
$\begin{align} \varphi(V_1,V_2,\cdot,V_n)=\prod_{i=0}^n \left(V_i+\sum_{U\in N(V_i)}U\right) \end{align}$
然后我一脸懵逼，然后查看了资料，原来是这样理解的：
其中的累加号表示对所有 $V_i$ 的邻接点求和，这里的求和就是或运算，乘积就是与运算。把公式按照布尔运算展开成与或式，则每一个乘积项代表是一个极小支配集。
选取 $V_i$ 表示为 $V_i=1$ ，不选 $V_i$ 表示为 $V_i=0$ 。
比如某个图有四个顶点，并且我们按照公式计算得到：
$\begin{align} \varphi(V_1,V_2,V_3,V_4)=V_1V_2+V_2V_3V_4 \end{align}$
然后我们指导要使 $\varphi(V_1,V_2,V_3,V_4)=1$ 则有两种组合可以选择： ${V_1,V_2\},\{V_2,V_3,V_4\}$
这样就可以得到所有的极小支配集。

但是那么为什么这样做就是合理呢？
为了叙述方便，我们令 $\varphi_i=V_i+\sum_{U\in N(V_i)}U$ ，则公式简写为 $\varphi=\prod_{i=0}^n \varphi_i$ 。
假设我们已经选取了一个点集 ${V_i\}$ 满足 $\varphi=1$ 的要求，不失一般性取图 $G$ 中的点 $V_j\notin\{V_i\}$ ，如果 $V_j$ 和点集 ${V_i\}$ 间没有边相连，那么 $\varphi_j$ 中就不包含点集 ${V_i\}$ ，带入 ${V_i\}$ 由于 $\varphi_j=0$ ，所以 $\varphi=0$ ，这样就和假设矛盾了。所以所有使得 $\varphi=1$ 的组合 ${V_i\}$ 都是支配集。
同样假如我们选中点集 ${V_i\}$ ，但 $\varphi=0$ ，那么至少有一个 $\varphi_j=0$ ，等于是说 $\varphi_j$ 中的点和我们选中的点集 ${V_i\}$ 之间没有连接，这样的话点集 ${V_i\}$ 显然就不是支配集了。
所以我们知道了： $\varphi=1\Longleftrightarrow \{V_i\}$ 是支配集。
最后从公式最后整理出来的与或式可以看出：任选一个乘积项将使得 $\varphi=1$ ，但乘积项中的点如果去除其中一个顶点（该顶点的值取 $0$ ）则 $\varphi=0$ ，因此乘积项就是极小支配集。

书上 $P 58$ 也给出了独立集、支配集、覆盖集之间的关系：

1. $I$ 是极大独立集 $\Longleftrightarrow$ $I$ 是独立支配集。
极大独立集为 $I$ 中，不在 $I$ 中的点必然连接到 $I$ 上（否则加入这些点就能构成更大的独立集），所以 $I$ 也是一个支配集，又 $I$ 是独立的，因此 $I$ 就是独立支配集。
反过来如果 $I$ 是支配集，点 $x\in V(G)-I$ 一定是通过边连接到 $I$ 中的，因此 $I+\{x\}$ 中有和 $x$ 邻接的顶点，但是加入 ${x\}$ 就破坏了原来的独立性，因此 $I$ 又是极大独立集。

2. $I$ 是独立集 $\Longleftrightarrow$ $V (G) - I$ 就是覆盖集。
显然如果 $I$ 是独立集，则对于 $I$ 的任意点 ${x\}$ 要么连接到 $V (G) - I$ 中，要么孤立，也就是说所有说图 $G$ 中的所有的边都是都和 $V (G) - I$ 中的点相关，因此 $V (G) - I$ 是覆盖集。
反过来 $V (G) - I$ 是覆盖集，所以所有的边至少有一个端点在 $V (G) - I$ 中，因此任意一条边不能两个端点都在 $I$ 中，也就是 $I$ 是独立集的意思。

3. $I$ 是极大（最大）独立集 $\Longleftrightarrow$ $V (G) - I$ 是极小（最小）覆盖集。
首先由性质 $2$ 可以看出 $V (G) - I$ 已经是覆盖集，由 $1$ 可知 $I$ 同时也是支配集，所以存在边 $(x, y)$ ，其中 $x\in I$ ， $y\in V(G)-I$ 。显然去掉 $V (G) - I$ 中的点 $y$ 则 $V (G) - I$ 没有点能够成为 $(x, y)$ 端点。因此 $V (G) - I$ 就是极小覆盖集。
反过来由 $2$ 可以看出 $I$ 是独立的，又 $V (G) - I$ 是极小覆盖集，如果在 $V (G) - I$ 中去掉一点 $x$ 后，就存在有一条边 $(x, y)$ 就不以 $V(G)-I-\{x\}$ 中的点为端点，也就是存在一条边它的两个端点都在 $I+\{x\}$ 中，也就是 $I$ 加入点 $x$ 之后有了相邻点，此时就它不是独立集了，因此 $I$ 是极大独立集。
我们就得到了： $I$ 是极大独立集 $\Longleftrightarrow$ $V (G) - I$ 是极小覆盖集。括号中的最大怎么解释呢？由于 $I$ 和 $V (G) - I$ 中顶点个数总和等于图 $G$ 顶点个数，因此如果 $I$ 的顶点数取最大等价于 $V (G) - I$ 的顶点数取最少，反之亦然。
这样就证明了这条性质。

4.极大独立集必为极小支配集。
极大独立集 $I$ 一定是支配集，并且是独立的，因此 $I$ 中的任意顶点 ${x\}$ 和 $I-\{x\}$ 中的顶点没有边连接，即 $I-\{x\}$ 不是支配集，也就是 $I$ 是极小支配集。

5.如果 $I$ 是独立集，则 $I$ 是极大独立集 $\Longleftrightarrow$ $I$ 极小支配集等价。
这个可以由性质 $1$ 和性质 $4$ 结合看出来。

然后书上又是给出了一个极小覆盖集的公式：
$\begin{align} \varphi(V_1,V_2,\cdot,V_n)=\prod_{i=0}^n \left(V_i+\prod_{U\in N(V_i)}U\right) \end{align}$
注意最里面是连乘号。

我们仿照极小支配集的思路来理解以下公式，极小这个事情显然可以通过最后的与或式来说明的，这里就不啰嗦了。我们来证明这个 $\varphi=1$ 等价于选取的点集 ${V_i\}$ 是极小覆盖。
同样我们记 $\varphi_i=V_i+\prod_{U\in N(V_i)}U$ ，那么公式简写为 $\varphi=\prod_{i=0}^n \varphi_i$ 。
假设我们选取了点集 ${V_i\}$ ，并且使得 $\varphi=1$ ，假设有一条边 $V_j,V_k)$ 没有被覆盖，则 $V_j,V_k$ 不属于点集 ${V_i\}$ ，那么 $\varphi_j$ 中的 $\prod_{U\in N(V_j)}U=0$ ，因为 $V_k$ 是 $V_j$ 的邻接点，乘积就包含了 $V_k$ ，而 $V_k\notin\{V_i\}$ ，即 $V_k=0$ ，同理有 $V_j=0$ ，因此 $\varphi_j=0$ ，这就导致 $\varphi=0$ ，和假设矛盾了。因此使得使得 $\varphi=1$ 的点集 ${V_i\}$ 一定是极小覆盖。
同样假如我们选中点集 ${V_i\}$ ，但 $\varphi=0$ ，那么至少有一个 $\varphi_j=0$ ，等于是说 ${V_i\}$ 不包含 $V_j$ ，且 $V_j$ 的邻接点中至少有一个顶点 $V_k$ 不属于 ${V_i\}$ ，因此 $V_j,V_k)$ 两个端点都不属于 ${V_i\}$ ，因此 ${V_i\}$ 不是覆盖集。
所以我们知道了： $\varphi=1\Longleftrightarrow \{V_i\}$ 是覆盖集。

六、最大网络流

比较困惑的地方在于，流 $F$ 是网络 $D$ 的一个流，如果不存在 $V_s$ 到 $V_t$ 的关于 $F$ 的可改进路 $P$ ，那么 $F$ 一定是一个最大流？
首先必要性是显然的，如果 $F$ 是最大流一定不能再改进，也就不可能找到可改进路 $P$ 了。

充分性的证明比较困难，需要系统学习一下切割的知识。

把图 $G$ 中的点分成两个阵营，一个包含原点 $V_s$ 记为 $S$ ，一个包含汇点 $V_t$ 记为 $T$ ，显然两则互补即： $\bar S=T$
从 $S$ 到 $T$ 的弧的集合就叫做一个割，简记为： $K = (S, T)$
定义割的容量：
$c(K)=\sum_{a\in K} c(a)$
如果网络流为 $f$ ，而整个网络流的值为 $f_{s,t}$ ，而 $(S, T)$ 是网络的一个割，则有：
$f_{s,t}=\sum_{a\in (S,T)} f(a)-\sum_{a'\in (T,S)}f(a')$
通常也简记为： $f_{s,t}=f (S,T)-f (T,S)$
它的意义很直观，就是流到汇点那边的流量的减去流回源点这边的流量=净流量。
下面来证明一下：
由流函数 $f$ 的性质：
$f[V_s,V(G)]-f[V(G),V_s]=f_{s,t}$
$f[V_i,V(G)]-f[V(G),V_i]=0$ ，其中 $V_i不为源点和汇点$
$f[V_t,V(G)]-f[V(G),V_t]=-f_{s,t}$
在割 $K = (S, T)$ 中有：
$\sum_{V_k\in S}\{f[V_k,V(G)]-f[V(G),V_k]\}=f_{s,t}$
简记为： $f[S,V(G)]-f[V(G),S]=f_{s,t}$ 。
由于 $V(G)=S\cup \bar S$ ，所以 $f[S,V(G)]=f(S,S)+f(S,\bar S)$ ，
同理 $f[V(G),S]=f(S,S)+f(\bar S,S)$ ，所以有：
$f(S,\bar S)-f(\bar S,S)=f_{s,t}$ ，这个式子就是我们要的结论： $f_{s,t}=f (S,T)-f (T,S)$ 。
显然如果对于任意一个割 $K = (S, T)$ 的容量来看， $(T,S)\le c(K)$
于是得到一个推论： $f_{max}\le c_{min}(K)$

最大流最小割定理：
这个就非常重要了，它的意思是 $f_{max} = c_{min}(K)$ 。
假设 $f$ 是一个最大流，我们来通过它定义各个割，采用逐步生成的方法来构造 $S$ 。
首先 $V_s\in S$ ，这样 $S$ 就不是空集了，然后对于顶点 $i\in S$ ，如果 $f (i, j) < c (i, j)$ 或者 $f (j, i) > 0$ ，则把 $j$ 加入到 $S$ 中。

理解一下这件事情，首先从无向图的观点看所有的加入点都能通过一系列的边连通到点 $V_s$ ，并且每一次 $S$ 向外拓展必然是加入了一条不饱和的弧（ $f (i, j) < c (i, j)$ 代表了弧的方向是从 $S$ 指向外面的，而 $f (j, i) > 0$ 反映弧是从外面指向 $S$ 的）。

显然 $V_t\notin S$ ，否者按照前面扩展 $S$ 的方式，随着 $S$ 的扩张就会出现一条从 $V_s$ 到 $V_t$ 的路，并且这条路上的弧
都是不饱和的弧，因此就出现了一条可改进路，这样 $f$ 就不是最大流了。

所以 $V_t\in \bar S$ ，所以 $(S,\bar S)$ 构成了一个割。
我们考察一条边从 $S$ 到 $\bar S$ 的边 $V_i,V_j)$ ，如果 $f(V_i,V_j)<c(V_i,V_j)$ ，那么按照 $S$ 的生成方法就有 $V_j\in S$ ，这样就矛盾了，因此必须有 $f(V_i,V_j)=c(V_i,V_j)$ 。
同理我们考察一条边从 $\bar S$ 到 $S$ 的边 $V_j,V_i)$ ，如果 $f(V_j,V_i)>0$ ，那么又会导致 $V_j\in S$ ，这样就矛盾了，因此必须有 $f(V_j,V_i)=0$ 。

因此对于最大流 $f$ 必有 $f_{s,t}=c(S,\bar S)$ ，先前我们知道了 $f_{max}\le c_{min}(K)$ ，现在我们来看总是可以取一些特殊的割使得最大流等于这个割，因此我们立刻就知道了，刚才构造的割其实是最小割，并且我们有： $f_{max}= c_{min}(K)$ 。

现在我们来看可改进路和最大流的充分关系了。
假设经某算法的操作得到了流 $f$ ，并且目前已经找不到可改进路了，此时我们按照定理证明过程中那样构造 $S$ ，那么显然 $V_t\notin S$ ，否则按照上面的推理就会出现可改进路。而定理的证明其实就是通过构造 $S$ 直接得到最小割 $c_{min}(K)$ ，因此此时的流 $f=c_{min}(K)$ ，根据定理这个流就是最大流。