符号间干扰(ISI)
模拟调制系统中,对于引起信号接受质量降级的主要因素,均强调了加性高斯白噪声干扰,对于数字基带传输还有一个会导致接收误码的重要因素是码间或符号间干扰(ISI)。其主要原因是,表示编码符号的窄脉冲波形系列的每一个脉冲需要很宽的信道带宽,而有限带宽的信道传输对于信号脉冲限带后,原来发送的这些信号脉冲必然在时域流散,它们会大大超越发送时的码元时间。相邻脉冲会在信道中互相拖尾混叠,在接收判决时,就可能导致误码。
+-----------+ +------------+ +---------------------+ +-----------+ +----------------+ +--------------+
| 信息源 | -> | 编码器 | -> | 脉冲成形滤波器 | -> | 信道 | -> | 接收滤波器 | -> | 采样判决 |
+-----------+ +------------+ +----------------------+ +-----------+ +----------------+ +--------------+
Source Bits: The original digital data (binary sequence).
Encoder: Adds redundancy for error correction (e.g., convolutional, LDPC).
Pulse Shaping Filter: Shapes the digital pulses to limit bandwidth and reduce ISI (commonly Root Raised Cosine (RRC) filter).
Channel: The transmission medium, which may add noise (AWGN), fading, or other impairments.
Receiver: Receives the signal, applies a matched filter (often matched to the transmit pulse shape), and samples at symbol rate.
Sampler & Decoder: Samples the filtered signal and decodes the bits, possibly using error correction.
Output Bits: The recovered digital data
+---------------------------------+ +-----------------+ +--------------------------+
| 脉冲成形滤波器 | -> | 信道
| -> | 接收滤波器
|
+---------------------------------+ +-----------------+ +--------------------------+
脉冲成形滤波器 和匹配滤波器
可以改善由于带宽限制导致的ISI, 但是由于
是未知的,或者信道为时变特性,传输信号会或多或少的残留不规则的拖尾。如多径衰落和非线性导致的信号幅度与相位的非线性失真,这里统称为残留ISI。因此需要对信号进行均衡处理。
均衡主要用于消除残留的码间干扰,通过对整个传输系统进行补偿。
单载波传输系统抗符号间干扰
定义 输出信号的波形形状为 ,则 传输系统不存在ISI 的条件应该满足的时域必要条件为:
这里为 为采样周期,
应该表示各个码元的抽样时刻,
表示当前抽样时刻,通过控制所有抽样时刻的拖尾实现避免ISI.
在频域分析其充分条件,
定义 为
的傅里叶变换,
为 抽样后离散序列
的傅里叶变换。
(证明见附一)
对于抽样时刻(m = 0)的频谱应为, 则
上述为奈奎斯特第一准则。
如果速率为Rb 的二进制序列的传输系统相应,以间隔 Tb = 1/Rb 进行定时抽样的频谱为常数,则无码间干扰。
可以看出,以上可以分为两种情况
(1) 信道响应频谱是带宽为 的理想低通特性,
,
如下图,当定时抽样后,将是一系列方波频谱,弥合成一条幅度为Tb的水平线。
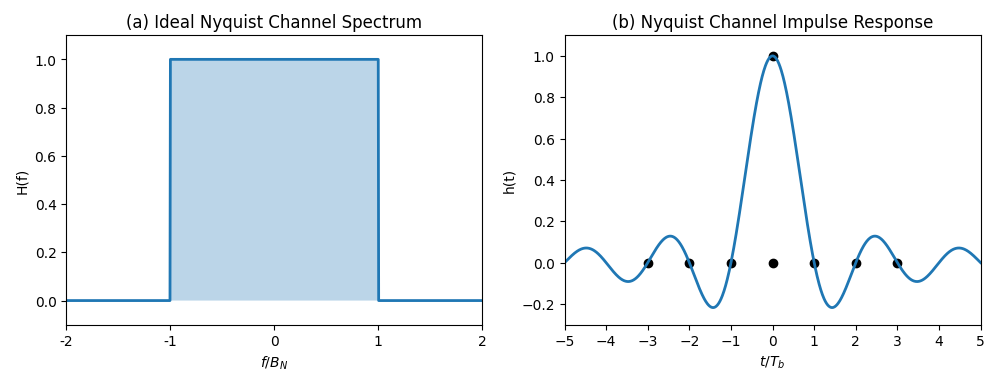
(2) 为了克服上述理性信道的不可实现性,将带宽 扩展至
,并满足无ISI 条件, 则,
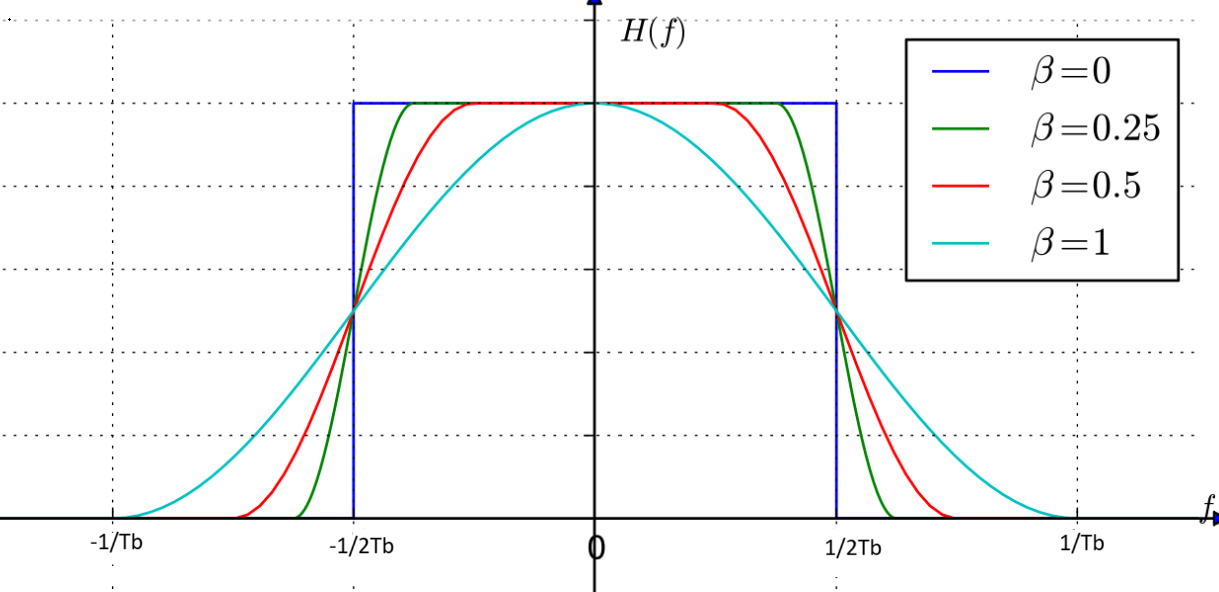
当 时,以Rb 抽样的频谱序列必然具有重叠性,则如果要满足重叠之和等于常数Tb,则需要满足互补对称的滚降特征的信号响应的频谱,如图中除去蓝线之外的线。我们将这种频谱特征成为升余弦频谱,这种函数形式包括平坦部分和滚降部分。
从图中可以看出,为保证互补对称性我们要求 滚降部分 线性映射到弦的半周期 [0, π];则余弦的系数
应保证
,则
,
同时将余弦函数平移 保证在
点处互补对称。 函数的形式可以表示为:
前面关于奈奎斯特准则消除符号间干扰,是以发送,信道和接收三者的滤波特性综合视为广义信道的基础上进行考虑的,在实际系统设计时,虽然对于广义信道的滤波特性很难估计,但是仍需要设计脉冲成形滤波器,使信号本身具有良好抗ISI的特性,增加系统ISI的鲁棒性。
OFDM 系统中的抗符号间干扰
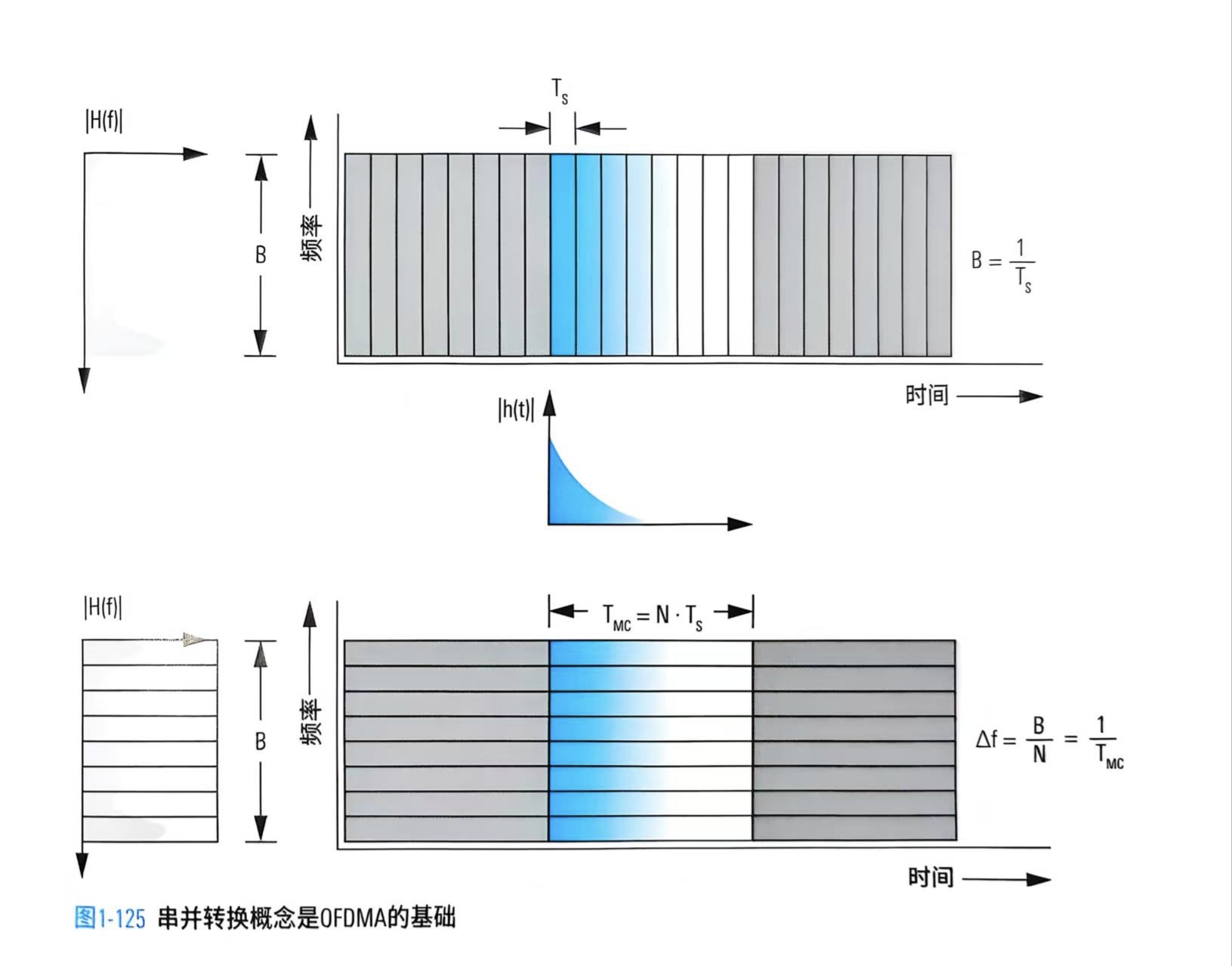
相对于上述单载波传输系统,OFDM系统为多载波传输系统,对于OFDM 调制符号本身而言,
其串并转换使其把并行的数据符号映射到窄带的频率子载波上,而不是将复杂的数据符号作为连续的时域信号发送。各个子载波上的符号长度增加,单个子载波的占用带宽很小,多载波占用的总带宽仍然很宽(仍为B),此时信道可以被当做平坦衰落而非频率选择性衰落。因此OFDM 符号本身具有一定的抗ISI的特性,
在实际的OFDM 系统中,发送端OFDM 符号生成是以快速傅里叶的逆变换实现的,其公式为
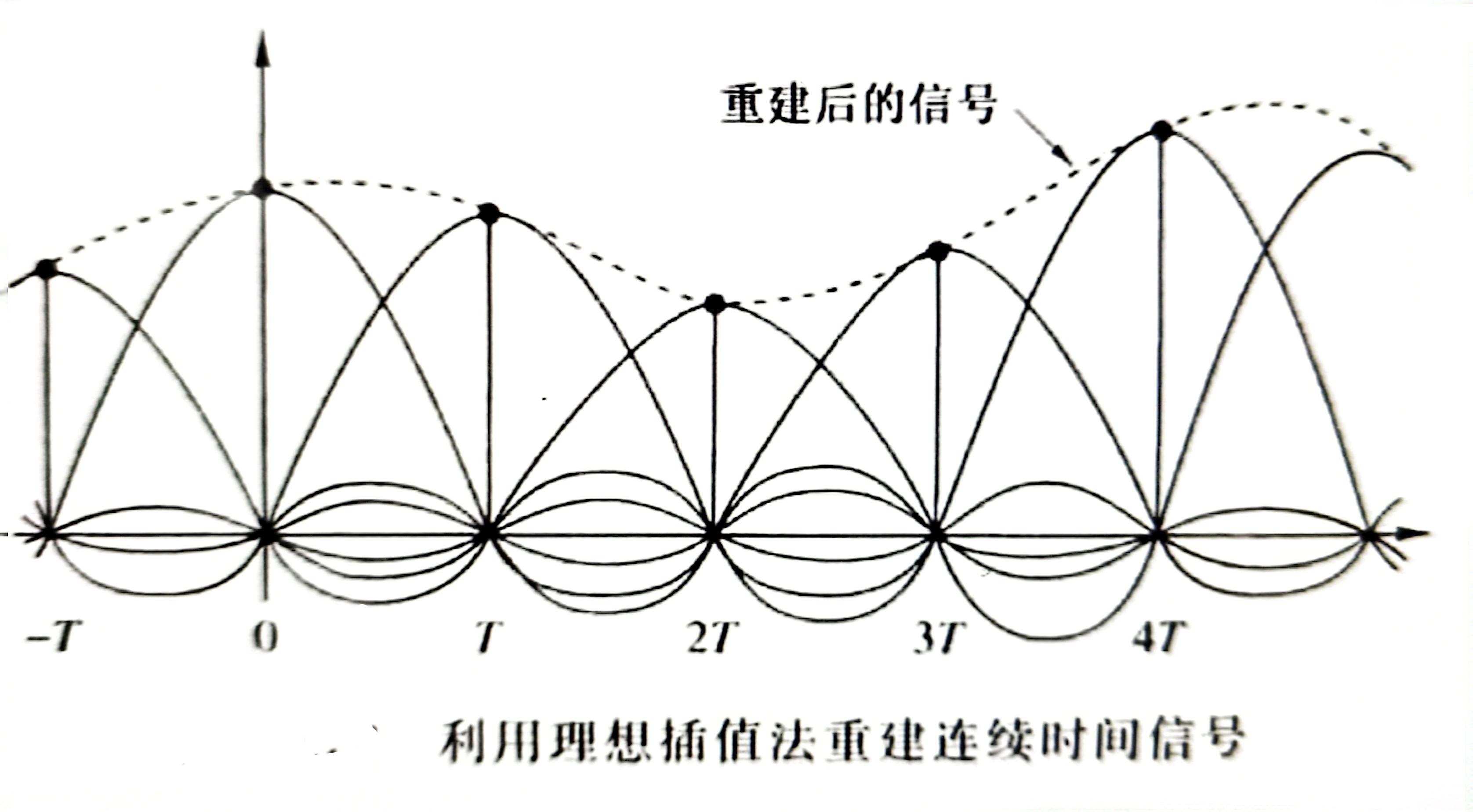
我们可以简单的运用数字域DFT 来生成OFDM符号,但是如果我们要在空口模拟信道中,需要进行模拟信号的重建,如附二,理想的信号重建需要无限长的sinc 函数,但是在实际情况中无法做到,当信号被截断为有限时长后,其频谱会发生变化。这种截断相当于将信号与一个矩形窗函数相乘,有限时长信号的频谱会变成原无限长信号频谱与sinc函数的卷积,从而使频谱主瓣加宽、旁瓣出现,超出理想带宽,造成频谱泄漏 ,如下图。
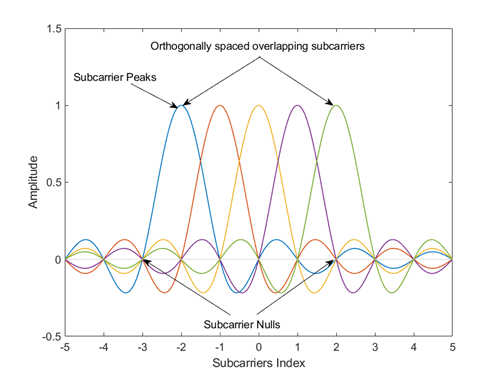
这种情况不只限于OFDM 系统中而是会发生在所有的数字信号的模拟重建的场景,此时频谱泄漏在发送端成为影响OFDM 信号质量的主要因素,因此在实际的OFDM传输系统中一定会加保护带宽。脉冲成型滤波器的主要作用不再是抗ISI,而是抑制带外辐射。而脉冲成型滤波器的设计不当,还会导致ISI。
在OFDM系统中,一种方法是插入空时段既保护间隔,这种方法有助于解决ISI的问题,但是由此产生的开关特性,会对功放的PAPR 产生负面影响,此外此方式还难以保持同步,OFDM 系统选择了另一种方案,称为(CP-OFDM),通过添加循环前缀(CP)来消除由于多径效应引起码间干扰。
信道均衡
在实际系统中,对于发送成形,接收滤波器等设计未必完善,对于信道真实特性缺乏真实了解,传输信号或多或少的会有残留的不规则波形拖尾,导致ISI影响,如多径衰落特性,加上非线性造成信号幅度与相位的非线性失真,也都是产生ISI的因素,统称为残留ISI,因此需要对接收信号进行均衡处理。
均衡主要是用于消除残留的码间干扰,对信道或整个传输系统特性进行补偿。实现均衡的方法根据不同的均衡算法来实现,通过自适应均衡实时的探测信道变化,来动态的进行补偿,常用的算法诸如迫零均衡算法,最小均方误差算法和递归最小二乘算法。
具体的均衡算法在后续篇章介绍。
附一: 信号采样频谱特性
该积分区间可以划分为无限多个宽度为1/Tb的区间之和
在
到
的值 与
在区间
到
的值相同,因此,
为周期为
的周期函数 , 根据DTFT 逆变换
这里是数字角频率 其和真实的频率之间的关系为
,
进一步 推算为
比较(1)和 (2)式
得
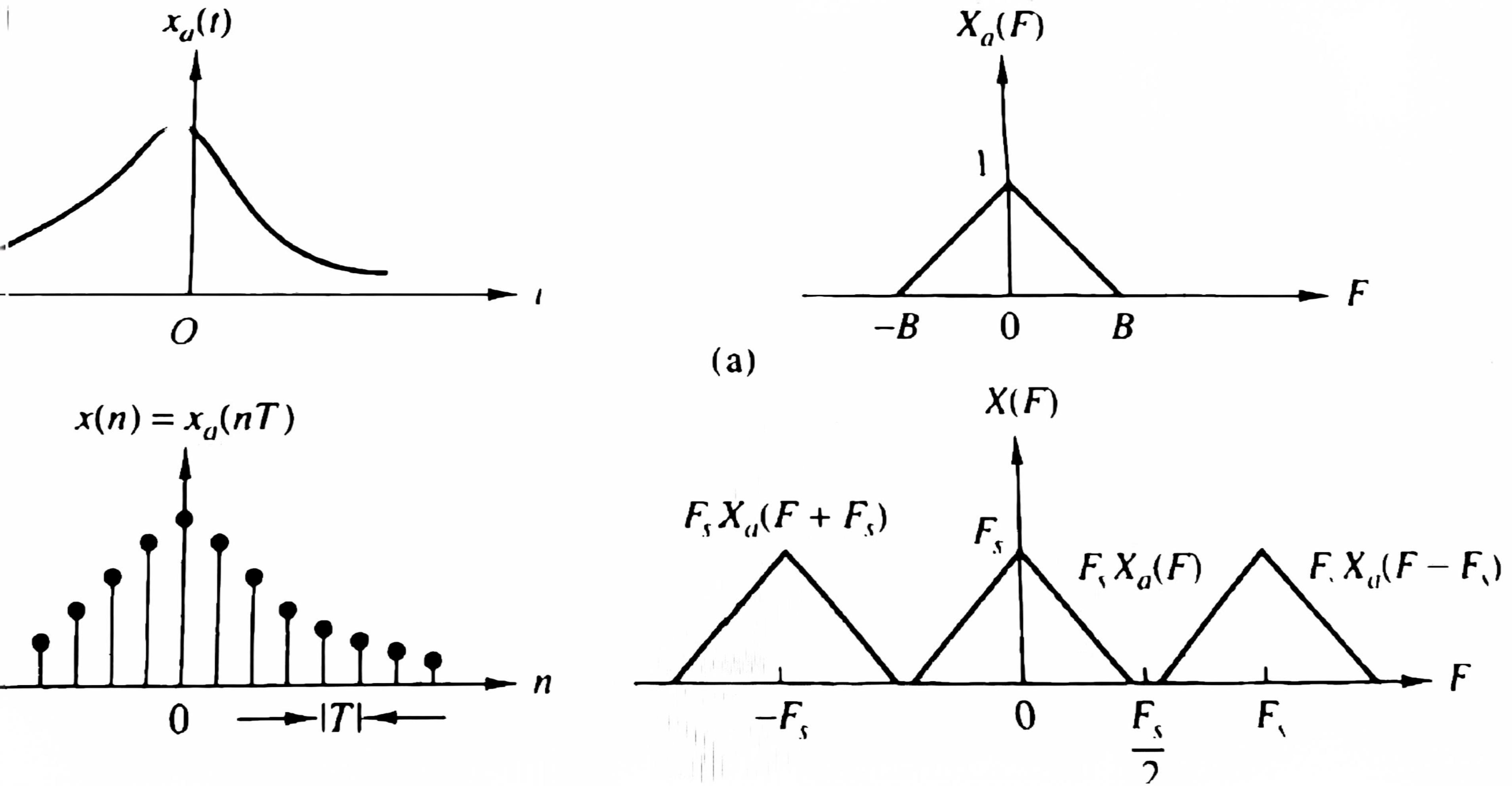
附二:信号重建
DTFT 逆变换为
由(1)和 (2)推得:






















 2947
2947

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








