线性均衡-峰值失真准则（迫零均衡滤波器）

最新推荐文章于 2025-10-06 09:59:38 发布

原创最新推荐文章于 2025-10-06 09:59:38 发布 · 482 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#算法

通信原理专栏收录该内容

6 篇文章

订阅专栏

峰值失真被简单定义为均衡器输出端的最坏情况码间干扰。使这一性能指标最小化的过程被称为峰值失真准则。我们首先考虑在均衡器具有无限多个抽头的情况下最小化峰值失真，然后再讨论横向均衡器跨度为有限时间的情况。

我们注意到，具有冲激响应的离散时间线性滤波器模型与具有冲激响应的均衡器级联后，可等效为一个具有冲激响应的单一滤波器：

即是与的卷积。假设均衡器有无限多个抽头，其在第 k 个采样时刻的输出可表示为

式中的第一项代表期望符号的缩放版本。为方便起见，我们将 q₀归一化为 1。第二项是码间干扰，该干扰的峰值被称为峰值失真，表达式为：

因此，D (c) 是均衡器抽头权重的函数。

对于具有无限多个抽头的均衡器，可以选择抽头权重使得 D (c) = 0，即对于除 n=0 外的所有 n，都有 qn=0，也就是说，码间干扰可以被完全消除。实现这一目标的抽头权重值由以下条件确定：

取 z 变换，可得

$Q(z) = C(z)F(z) = 1$

其中，C (z) 表示的 z 变换。需要注意的是，传递函数为 C (z) 的均衡器其实就是线性滤波器模型 F (z) 的逆滤波器。换言之，要完全消除码间干扰，需要使用 F (z) 的逆滤波器，我们将这种滤波器称为迫零滤波器。下图展示了带迫零均衡器的信道框图。

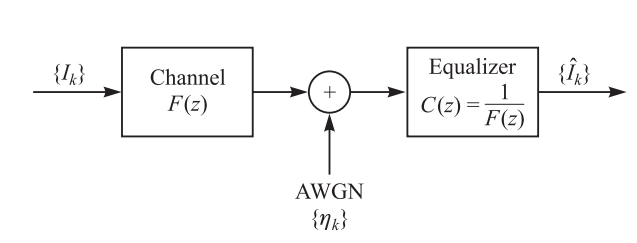
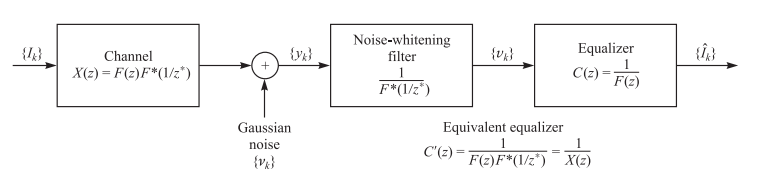
具有传递函数的与白化滤波器与具有传递函数的迫零均衡器级联后，形成一个等效的迫零均衡器，其传递函数为：

该组合滤波器的输入是来自匹配滤波器的采样序列，其输出仅包含受加性零均值高斯噪声干扰的期望符号。组合滤波器的冲激响应为：

完全消除码间干扰的无限抽头均衡器的性能可以用其输出端的信噪比来表示。为了数学计算方便，我们将接收信号能量归一化为 1。这意味着 q₀=1，且 | I_k|² 的期望值也为 1。此时，信噪比就是均衡器输出端噪声方差 σₙ² 的倒数。

从图中可以观察，噪声白化滤波器的输入前会经过模拟滤波器匹配输入信号并采样,对匹配滤波器输出采样分析，为获取最大SNR, 匹配滤波器的冲击响应

则匹配滤波器的输出为 $r_k = \int_{-\infty}^{\infty} h^*(t)h(t + kT) dt$ ，同时需要满足无码间干扰条件 $R(z) * C ^{'} (z)= 1$ ，可以得到 $x_k = \int_{-\infty}^{\infty} h^*(t)h(t + kT) dt$ 。

由Parseval 定理可以得到：

进一步推导：

同时

$x_k= \int_{-\pi/T}^{\pi/T}{X(e^{jwT})}e^{jwkT}dw$

则得

$X(e^{jwT})= \left( \sum_{n=-\infty}^{\infty} \left| H\left( \omega + \frac{2\pi n}{T} \right) \right|^2 \right)$ （1）

白噪声在等效均衡器的输入的功率谱密度为

输出则为

噪声变量的方差为

（2）

由（1）和（2）得到均衡器的 SNR 为

$\gamma_{\infty} = \frac{1}{\sigma_n^2} = \left( \frac{TN_0}{2\pi} \int_{-\pi/T}^{\pi/T} \frac{d\omega}{X(e^{j\omega T})} \right)^{-1}$

$=\left( \frac{T^2 N_0}{2\pi} \int_{-\pi/T}^{\pi/T} \frac{d\omega}{\sum_{n=-\infty}^{\infty} |H(\omega + 2\pi n/T)|^2} \right)^{-1}$

从以上的公式推理可以观察到

如果折叠频谱 $\left( \sum_{n=-\infty}^{\infty} \left| H\left( \omega + \frac{2\pi n}{T} \right) \right|^2 \right)$ 在某个频点 $w_0$ 处为零（即信道存在频谱零点），为满足“迫零”条件 $(C'(z) = \frac{1}{X(z)})$ ，均衡器需要引入无限大的增益，以补偿信道衰减。