机器学习技法 作业四

1 计算一次前向加一次后向的总计算次数。网络结构641，前向63+41次，后向4（w2的梯度）+3（隐藏层的delta）+3*6（w1的梯度），一共47次。

2 36个隐藏层，每个有一个单元的时候系数最少。46个。要说为啥这样最少也说不上来为啥，大致就是每一层的系数需要相乘，每一个要乘的项越小最后结果越小吧。或者可以编程遍历所有情况计算。

3 与上一题相反，让相乘的式子里数字比较大的时候系数最多。当有两个18个单元的隐藏层时最多，超过520个。

4 矩阵求导。水平不过关，贴一个其他人的解答过程：

题目如下：


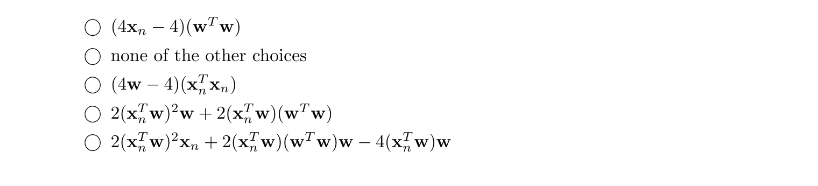
5 把括号展开即可。中间一项只有一个一次方的噪声，求期望之后为0。因此剩下两个平方项，选第四项：

6 最近邻1个点，相当于分界线是两个点连线的中垂线。因此算一下中垂线即可，选第三项：

7 RBF网络与线性模型等价，因此两个模型同时大于0的范围相同，基于此用$g_{RBFNET}(x)>0$然后整理形式为线性，对应上w与b即可，选第一项：

8 RBF网络系数的求法。用的是线性回归直接解析解的形式。即：

每个x都不同，因此Z可逆。由于RBF比较特殊，因此得到的Z是一个单位矩阵。系数$\beta$最终结果就是$y_n$。


9 用$V^{T}W$来对$R$进行回归操作。对目标函数对于$w_m$进行求导：

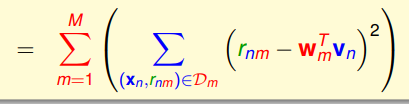
得到： 2 ∑ ( x n , r n m ) ∈ D m ( r n m − w m T v n ) v n = 0 → w m = ∑ n r n m ∑ n 1 2\sum_{(x_n,r_{nm})\in D_m}(r_{nm}-w_m^Tv_n)v_n=0\to w_m=\frac{\sum_n r_{nm}}{\sum_n 1}