机器学习技法作业链接
我做的是Machine Learning, Spring 2019。目前Bonus(17、18)没做。已做内容有一些存疑,格式和内容待优化。欢迎指出问题。
Transforms: Explicit versus Implicit
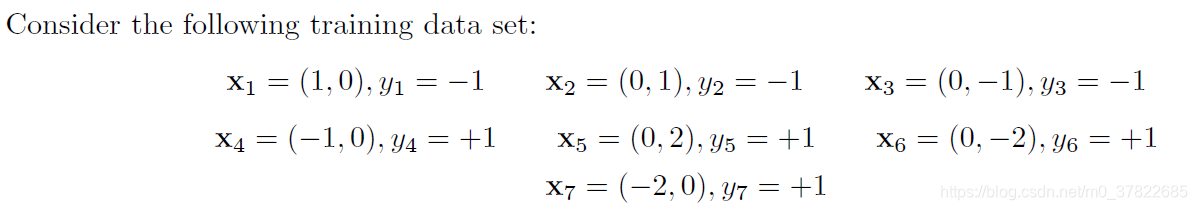
1)
import numpy as np
import matplotlib.pyplot as plt
x = np.asarray([[1, 0], [0, 1], [0, -1], [-1, 0], [0, 2], [0, -2], [-2, 0]])
y = [-1, -1, -1, 1, 1, 1, 1]
z1 = 2 * (x[:, 1] ** 2) - 4 * x[:, 0] + 2
z2 = x[:, 0] ** 2 -2 * x[:, 1] - 3
z = [[z1[i], z2[i]] for i in range(len(x))]
plt.scatter(z1[:3], z2[:3], label="-1")
plt.scatter(z1[3:], z2[3:], label="+1")
plt.xlabel("z1")
plt.ylabel("z2")
plt.legend()
plt.plot([5, 5], [-7, 1])
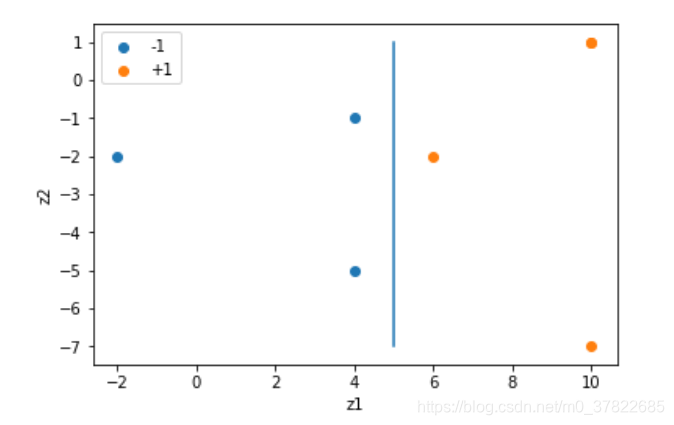
2)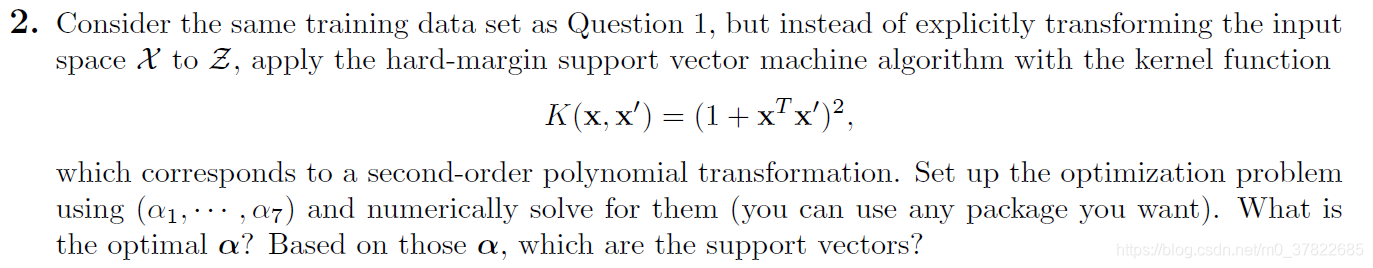
from sklearn import svm
x = np.asarray([[1, 0], [0, 1], [0, -1], [-1, 0], [0, 2], [0, -2], [-2, 0]])
y = [-1, -1, -1, 1, 1, 1, 1]
clf = svm.SVC(C=1e100, kernel='poly', degree=3, gamma=1, coef0=1)
clf.fit(x, y)
alpha = clf.dual_coef_
sv = clf.support_vectors_

g
s
v
m
(
x
1
,
x
2
)
=
s
i
g
n
(
−
0.29096704
(
1
+
x
2
)
2
)
−
0.29094205
(
1
−
x
2
)
2
+
0.38089797
(
1
−
x
1
)
2
+
0.10050786
(
1
+
2
x
2
)
2
+
0.10050326
(
1
+
2
x
2
)
2
)
−
1.66606947
g_{svm}(x_1,x_2) = sign(-0.29096704(1+x_2)^2)-0.29094205(1-x_2)^2 +0.38089797(1-x_1)^2 \\ +0.10050786(1+2x_2)^2+0.10050326(1+2x_2)^2)-1.66606947
gsvm(x1,x2)=sign(−0.29096704(1+x2)2)−0.29094205(1−x2)2+0.38089797(1−x1)2+0.10050786(1+2x2)2+0.10050326(1+2x2)2)−1.66606947
3)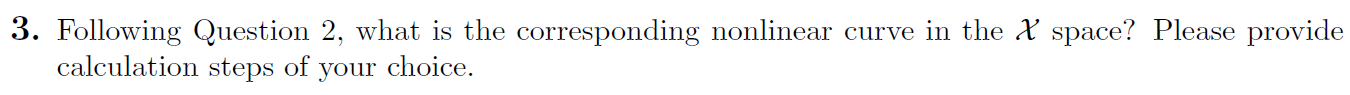
def get_weight(alpha, sv):
w = np.zeros(6)
for i in range(len(sv)):
wi = np.asarray([1,
2 * sv[i][0],
2 * sv[i][1],
2 * sv[i][0] * sv[i][1],
sv[i][0] ** 2,
sv[i][1] ** 2])
w = w + alpha[0][i] * wi
return w
def z(w, b, x1, x2):
return w[0] + w[1]*x1 + w[2]*x2 + w[3]*x1*x2 + w[4]*(x1**2) + w[5]*(x2**2) + b
w = get_weight(alpha, sv)
b = clf.intercept_
x1 = np.linspace(-2, 2, 2000)
x2 = np.linspace(-2, 2, 2000)
X1, X2 = np.meshgrid(x1, x2)
plt.scatter(x[:3, 0], x[:3, 1], label="-1")
plt.scatter(x[3:, 0], x[3:, 1], label="+1")
plt.contour(X1, X2, z(w, b, X1, X2))
plt.xlabel("x1")
plt.ylabel("x2")
plt.legend()
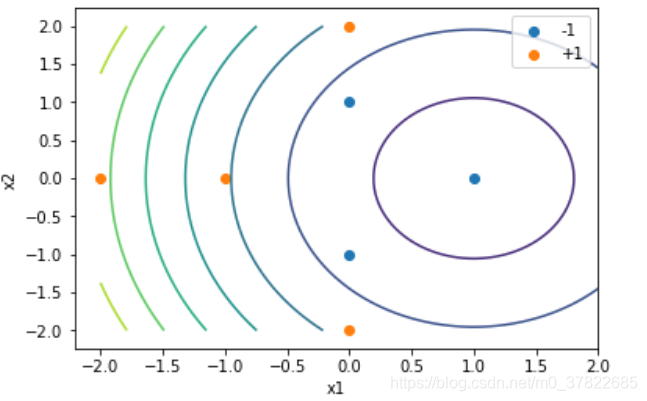
4)
不一样,1)相当于把二维数据转换到另一个二维空间中,3)是隐射到6维空间
Kernels and Transforms
5)
要证
e
x
p
(
−
x
2
)
=
1
∣
∣
ϕ
(
x
)
~
∣
∣
exp(-x^2)=\frac{1}{||\tilde{\phi(x)}||}
exp(−x2)=∣∣ϕ(x)~∣∣1
只需证
e
x
p
(
x
2
)
=
∣
∣
ϕ
~
(
x
)
∣
∣
exp(x^2)=||\tilde{\phi}(x)||
exp(x2)=∣∣ϕ~(x)∣∣
只需证
e
x
p
(
2
x
2
)
=
∣
∣
ϕ
~
(
x
)
∣
∣
2
exp(2x^2)=||\tilde{\phi}(x)||^2
exp(2x2)=∣∣ϕ~(x)∣∣2
e
x
p
(
2
x
2
)
=
∑
i
=
0
+
∞
2
i
i
!
⋅
x
i
=
∣
∣
ϕ
~
(
x
)
∣
∣
2
exp(2x^2)=\sum_{i=0}^{+\infty}\frac{2^i}{i!}\cdot x^i=||\tilde{\phi}(x)||^2
exp(2x2)=i=0∑+∞i!2i⋅xi=∣∣ϕ~(x)∣∣2
∴
证
毕
\therefore 证毕
∴证毕
这题告诉我们
ϕ
(
x
)
=
ϕ
~
(
x
)
∣
ϕ
~
(
x
)
∣
\phi(x)=\frac{\tilde{\phi}(x)}{|\tilde{\phi}(x)|}
ϕ(x)=∣ϕ~(x)∣ϕ~(x)
6)
cos
(
x
,
x
’
)
=
x
⋅
x
′
∣
x
∣
∣
x
′
∣
=
x
∣
x
∣
⋅
x
′
∣
x
′
∣
=
ϕ
(
x
)
T
ϕ
(
x
′
)
\cos(x,x^{’})=\frac{x\cdot x^{'}}{|x||x^{'}|}=\frac{x}{|x|} \cdot \frac{x^{'}}{|x^{'}|} = \phi(x)^T\phi(x^{'})
cos(x,x’)=∣x∣∣x′∣x⋅x′=∣x∣x⋅∣x′∣x′=ϕ(x)Tϕ(x′)
其中
ϕ
(
x
)
=
x
∣
x
∣
\phi(x)=\frac{x}{|x|}
ϕ(x)=∣x∣x,
x
x
x不为0向量
K
=
[
x
1
⋅
x
1
∣
x
1
∣
∣
x
2
∣
x
1
⋅
x
2
∣
x
1
∣
∣
x
2
∣
⋯
x
1
⋅
x
n
∣
x
1
∣
∣
x
n
∣
x
2
⋅
x
1
∣
x
2
∣
∣
x
1
∣
x
2
⋅
x
2
∣
x
2
∣
∣
x
2
∣
⋯
x
2
⋅
x
n
∣
x
1
∣
∣
x
n
∣
⋮
⋮
⋱
⋮
x
n
⋅
x
1
∣
x
n
∣
∣
x
1
∣
x
n
⋅
x
2
∣
x
n
∣
∣
x
2
∣
⋯
x
n
⋅
x
n
∣
x
n
∣
∣
x
n
∣
]
=
[
x
1
∣
x
1
∣
x
2
∣
x
2
∣
⋮
x
n
∣
x
n
∣
]
[
x
1
∣
x
1
∣
,
x
2
∣
x
2
∣
,
⋯
,
x
n
∣
x
n
∣
]
=
X
X
T
K= \left[ \begin{matrix} \frac{x_1 \cdot x_1}{|x_1||x_2|} & \frac{x_1 \cdot x_2}{|x_1||x_2|} & \cdots & \frac{x_1 \cdot x_n}{|x_1||x_n|}\\ \frac{x_2 \cdot x_1}{|x_2||x_1|} & \frac{x_2 \cdot x_2}{|x_2||x_2|} & \cdots & \frac{x_2 \cdot x_n}{|x_1||x_n|}\\ \vdots & \vdots & \ddots & \vdots\\ \frac{x_n \cdot x_1}{|x_n||x_1|} & \frac{x_n \cdot x_2}{|x_n||x_2|} & \cdots & \frac{x_n \cdot x_n}{|x_n||x_n|} \end{matrix} \right]= \left[\begin{matrix}\frac{x_1}{|x_1|}\\ \frac{x_2}{|x_2|}\\ \vdots \\ \frac{x_n}{|x_n|} \end{matrix} \right] \left[\begin{matrix}\frac{x_1}{|x_1|},\frac{x_2}{|x_2|},\cdots,\frac{x_n}{|x_n|} \end{matrix} \right] =XX^T
K=⎣⎢⎢⎢⎢⎡∣x1∣∣x2∣x1⋅x1∣x2∣∣x1∣x2⋅x1⋮∣xn∣∣x1∣xn⋅x1∣x1∣∣x2∣x1⋅x2∣x2∣∣x2∣x2⋅x2⋮∣xn∣∣x2∣xn⋅x2⋯⋯⋱⋯∣x1∣∣xn∣x1⋅xn∣x1∣∣xn∣x2⋅xn⋮∣xn∣∣xn∣xn⋅xn⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡∣x1∣x1∣x2∣x2⋮∣xn∣xn⎦⎥⎥⎥⎥⎤[∣x1∣x1,∣x2∣x2,⋯,∣xn∣xn]=XXT
对于任意不为0的实列向量
M
=
[
a
1
,
a
2
,
⋯
,
a
n
]
T
M=[a_1, a_2, \cdots, a_n]^T
M=[a1,a2,⋯,an]T,
M
T
K
M
=
(
M
T
X
)
(
X
T
M
)
=
(
a
1
x
1
∣
x
1
∣
+
a
2
x
2
∣
x
2
∣
⋯
a
n
x
n
∣
x
n
∣
)
2
≥
0
M^TKM=(M^TX)(X^TM)=(\frac{a_1x_1}{|x_1|}+\frac{a_2x_2}{|x_2|}\cdots \frac{a_nx_n}{|x_n|})^2 \ge 0
MTKM=(MTX)(XTM)=(∣x1∣a1x1+∣x2∣a2x2⋯∣xn∣anxn)2≥0
∴
K
半
是
正
定
矩
阵
\therefore K半是正定矩阵
∴K半是正定矩阵
又因为K是对称矩阵,所以当x不为0向量时,
c
o
s
(
x
,
x
’
)
cos(x,x^{’})
cos(x,x’)是一个有效的核函数。
Radius of Transformed Vectors via the Kernel

7)
L ( R , c , λ ) = R 2 + ∑ n = 1 N λ n ( ∣ ∣ z n − c ∣ ∣ 2 − R 2 ) L(R,c,\lambda)=R^2+\sum \limits_{n=1}\limits^{N} \lambda_n(||z_n-c||^2-R^2) L(R,c,λ)=R2+n=1∑Nλn(∣∣zn−c∣∣2−R2)
8)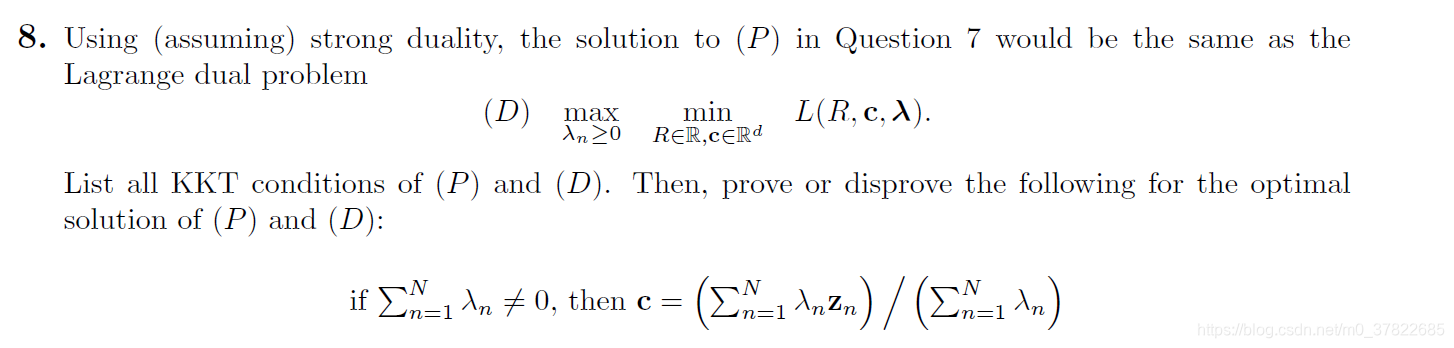
primal feasible:
∣
∣
z
n
−
c
∣
∣
2
≤
R
2
||z_n-c||^2 \le R^2
∣∣zn−c∣∣2≤R2
dual feasible:
λ
n
≥
0
\lambda_n \ge0
λn≥0
dual-inner optimal:
令
∂
L
(
R
,
c
,
λ
)
∂
R
=
2
R
−
2
R
∑
n
=
1
N
λ
n
=
0
⟹
∑
n
=
1
N
λ
n
=
1
\frac{\partial L(R,c,\lambda)}{\partial R} = 2R-2R\sum \limits_{n=1}\limits^N\lambda_n=0 \implies \sum \limits_{n=1}\limits^N\lambda_n=1
∂R∂L(R,c,λ)=2R−2Rn=1∑Nλn=0⟹n=1∑Nλn=1
∂
L
(
R
,
c
,
λ
)
∂
c
i
=
∑
n
=
1
N
2
λ
n
(
−
z
n
,
i
+
c
i
)
⟹
∂
L
(
R
,
c
,
λ
)
∂
c
=
∑
n
=
1
N
2
λ
n
(
−
z
n
+
c
)
\frac{\partial L(R,c,\lambda)}{\partial c_i} = \sum \limits_{n=1}\limits^N2\lambda_n(-z_{n,i}+c_i) \implies \frac{\partial L(R,c,\lambda)}{\partial c} =\sum \limits_{n=1}\limits^N2\lambda_n(-z_n+c)
∂ci∂L(R,c,λ)=n=1∑N2λn(−zn,i+ci)⟹∂c∂L(R,c,λ)=n=1∑N2λn(−zn+c)
令
∂
L
(
R
,
c
,
λ
)
∂
c
=
∑
n
=
1
N
2
λ
n
(
−
z
n
+
c
)
=
0
⟹
c
∑
n
=
1
N
λ
n
=
∑
n
=
1
N
λ
n
z
n
\frac{\partial L(R,c,\lambda)}{\partial c} =\sum \limits_{n=1}\limits^N2\lambda_n(-z_n+c)=0 \implies c\sum\limits_{n=1}\limits^{N}\lambda_n=\sum\limits_{n=1}\limits^{N}\lambda_n z_n
∂c∂L(R,c,λ)=n=1∑N2λn(−zn+c)=0⟹cn=1∑Nλn=n=1∑Nλnzn
primal-inner optimal:
λ
n
(
∣
∣
z
n
−
c
∣
∣
2
−
R
2
)
=
0
\lambda_n(||z_n-c||^2 - R^2)=0
λn(∣∣zn−c∣∣2−R2)=0
由
c
∑
n
=
1
N
λ
n
=
∑
n
=
1
N
λ
n
z
n
c\sum\limits_{n=1}\limits^{N}\lambda_n=\sum\limits_{n=1}\limits^{N}\lambda_n z_n
cn=1∑Nλn=n=1∑Nλnzn和
∑
n
=
1
N
λ
n
=
1
⟹
c
=
∑
n
=
1
N
λ
n
z
n
\sum\limits_{n=1}\limits^{N}\lambda_n =1 \implies c = \sum\limits_{n=1}\limits^{N}\lambda_n z_n
n=1∑Nλn=1⟹c=n=1∑Nλnzn
9)
min R ∈ R , c ∈ R d max λ n ≥ 0 R 2 + ∑ n = 1 N λ n ( ∣ ∣ z n − c ∣ ∣ 2 − R 2 ) = max λ n ≥ 0 min R ∈ R , c ∈ R d R 2 + ∑ n = 1 N λ n ( ∣ ∣ z n − c ∣ ∣ 2 − R 2 ) = max λ n ≥ 0 ∑ n = 1 N λ n ( ∣ ∣ z n − c ∣ ∣ 2 ) = max λ n ≥ 0 ∑ n = 1 N λ n ( ∣ ∣ z n − ∑ m = 1 N λ m z m ∣ ∣ 2 ) s . t ∑ n = 1 N λ n = 1 \begin{aligned} &\min\limits_{R \in \Bbb R,c \in \Bbb R^d}\max\limits_{\lambda_n \ge 0} R^2+\sum \limits_{n=1}\limits^{N} \lambda_n(||z_n-c||^2-R^2) \\ &= \max\limits_{\lambda_n \ge 0} \min\limits_{R \in \Bbb R,c \in \Bbb R^d} R^2+\sum \limits_{n=1}\limits^{N} \lambda_n(||z_n-c||^2-R^2)\\ &=\max\limits_{\lambda_n \ge 0}\sum \limits_{n=1}\limits^{N} \lambda_n(||z_n-c||^2)\\ &=\max\limits_{\lambda_n \ge 0}\sum \limits_{n=1}\limits^{N}\lambda_n(||z_n-\sum\limits_{m=1}\limits^{N}\lambda_m z_m||^2)\\ &s.t \ \ \sum\limits_{n=1}\limits^{N}\lambda_n =1 \end{aligned} R∈R,c∈Rdminλn≥0maxR2+n=1∑Nλn(∣∣zn−c∣∣2−R2)=λn≥0maxR∈R,c∈RdminR2+n=1∑Nλn(∣∣zn−c∣∣2−R2)=λn≥0maxn=1∑Nλn(∣∣zn−c∣∣2)=λn≥0maxn=1∑Nλn(∣∣zn−m=1∑Nλmzm∣∣2)s.t n=1∑Nλn=1
10)
max
λ
n
≥
0
∑
n
=
1
N
λ
n
(
∣
∣
z
n
−
∑
m
=
1
N
λ
m
z
m
∣
∣
2
)
=
−
min
λ
n
≥
0
∑
n
=
1
N
λ
n
(
∣
∣
z
n
−
∑
m
=
1
N
λ
m
z
m
∣
∣
2
)
=
min
λ
n
≥
0
∑
n
=
1
N
(
∑
m
=
1
N
λ
n
λ
m
z
n
T
z
m
−
λ
n
z
n
T
z
n
)
=
min
λ
n
≥
0
∑
n
=
1
N
∑
m
=
1
N
λ
n
λ
m
K
(
x
n
,
x
m
)
−
∑
n
=
1
N
λ
n
K
(
x
n
,
x
n
)
s
.
t
∑
n
=
1
N
λ
n
=
1
,
λ
n
≥
0
\begin{aligned} &\max\limits_{\lambda_n \ge 0}\sum \limits_{n=1}\limits^{N}\lambda_n(||z_n-\sum\limits_{m=1}\limits^{N}\lambda_m z_m||^2) \\ &=-\min\limits_{\lambda_n \ge 0}\sum \limits_{n=1}\limits^{N}\lambda_n(||z_n-\sum\limits_{m=1}\limits^{N}\lambda_m z_m||^2) \\ &=\min\limits_{\lambda_n \ge 0}\sum \limits_{n=1}\limits^{N}(\sum \limits_{m=1}\limits^{N}\lambda_n\lambda_mz_n^Tz_m - \lambda_nz_n^Tz_n) \\ &=\min\limits_{\lambda_n \ge 0}\sum \limits_{n=1}\limits^{N}\sum \limits_{m=1}\limits^{N}\lambda_n\lambda_m K(x_n,x_m) - \sum \limits_{n=1}\limits^{N}\lambda_nK(x_n,x_n)\\ &s.t \ \ \sum\limits_{n=1}\limits^{N}\lambda_n =1,\lambda_n \geq 0 \end{aligned}
λn≥0maxn=1∑Nλn(∣∣zn−m=1∑Nλmzm∣∣2)=−λn≥0minn=1∑Nλn(∣∣zn−m=1∑Nλmzm∣∣2)=λn≥0minn=1∑N(m=1∑NλnλmznTzm−λnznTzn)=λn≥0minn=1∑Nm=1∑NλnλmK(xn,xm)−n=1∑NλnK(xn,xn)s.t n=1∑Nλn=1,λn≥0
然后用二次规划求
λ
\lambda
λ.
二次项系数
q
n
,
m
=
K
(
x
n
,
x
m
)
q_{n,m}=K(x_n,x_m)
qn,m=K(xn,xm)
一次项系数
p
n
=
K
(
x
n
,
x
n
)
p_n=K(x_n,x_n)
pn=K(xn,xn)
a
≥
=
1
,
a
≤
=
−
1
,
a
n
T
是
长
度
为
N
,
第
n
个
位
置
为
1
,
其
余
位
置
为
0
的
向
量
a_{\geq}=1, a_{\leq}=-1,a_n^T是长度为N,第n个位置为1,其余位置为0的向量
a≥=1,a≤=−1,anT是长度为N,第n个位置为1,其余位置为0的向量
c
≥
=
1
,
c
≤
=
−
1
,
c
n
=
0
c_{\geq}=1, c_{\leq}=-1, c_n=0
c≥=1,c≤=−1,cn=0
可以根据上面得到
Q
,
p
,
A
,
c
Q,p,A,c
Q,p,A,c四个矩阵:
Q
=
[
K
(
x
1
,
x
1
)
⋯
K
(
x
1
,
x
N
)
K
(
x
2
,
x
1
)
⋯
K
(
x
2
,
x
N
)
⋮
⋮
⋮
K
(
x
N
,
x
1
)
⋯
K
(
x
N
,
x
N
)
]
Q= \left[ \begin{matrix} K(x_1,x_1) & \cdots & K(x_1,x_N) \\ K(x_2,x_1) & \cdots & K(x_2,x_N) \\ \vdots & \vdots & \vdots \\ K(x_N,x_1) & \cdots & K(x_N,x_N) \end{matrix} \right]
Q=⎣⎢⎢⎢⎡K(x1,x1)K(x2,x1)⋮K(xN,x1)⋯⋯⋮⋯K(x1,xN)K(x2,xN)⋮K(xN,xN)⎦⎥⎥⎥⎤
p
=
[
K
(
x
1
,
x
1
)
K
(
x
2
,
x
2
)
⋮
K
(
x
N
,
x
N
)
]
p= \left[ \begin{matrix} K(x_1,x_1) \\ K(x_2,x_2) \\ \vdots \\ K(x_N,x_N) \end{matrix} \right]
p=⎣⎢⎢⎢⎡K(x1,x1)K(x2,x2)⋮K(xN,xN)⎦⎥⎥⎥⎤
A
=
[
(
1
N
)
T
(
−
1
N
)
T
I
N
×
N
]
A= \left[ \begin{matrix} (1_N)^T\\ (-1_N)^T\\ I_{N \times N} \\ \end{matrix} \right]
A=⎣⎡(1N)T(−1N)TIN×N⎦⎤
c
=
[
1
−
1
0
N
]
c= \left[ \begin{matrix} 1\\ -1\\ 0_N\\ \end{matrix} \right]
c=⎣⎡1−10N⎦⎤
(
(
1
N
)
T
=
[
1
,
1
,
⋯
,
1
]
,
N
个
1
,
其
他
类
似
的
同
理
)
((1_N)^T=[1,1,\cdots,1],N个1,其他类似的同理)
((1N)T=[1,1,⋯,1],N个1,其他类似的同理)
用
Q
,
p
,
A
,
c
Q,p,A,c
Q,p,A,c解QP问题可得
λ
\lambda
λ的值。
λ
i
>
0
时
,
由
λ
i
(
∣
∣
z
i
−
c
∣
∣
2
−
R
2
)
=
0
知
,
∣
∣
z
i
−
c
∣
∣
2
−
R
2
=
0
,
\lambda_i >0时,由\lambda_i(||z_i-c||^2-R^2)=0知,||z_i-c||^2-R^2=0,
λi>0时,由λi(∣∣zi−c∣∣2−R2)=0知,∣∣zi−c∣∣2−R2=0,
则
R
=
∣
∣
z
i
−
c
∣
∣
=
∣
∣
z
i
−
∑
n
=
1
N
λ
n
z
n
∣
∣
=
z
i
T
z
i
−
2
∑
n
=
1
N
λ
n
z
i
T
z
n
+
∑
n
=
1
N
∑
m
=
1
N
λ
n
λ
m
z
n
T
z
m
=
K
(
x
i
,
x
i
)
−
2
∑
n
=
1
N
λ
n
K
(
x
i
,
x
n
)
+
∑
n
=
1
N
∑
m
=
1
N
λ
n
λ
m
K
(
x
n
,
x
m
)
\begin{aligned} R&=||z_i-c||=||z_i-\sum\limits_{n=1}\limits^{N}\lambda_n z_n||\\&=\sqrt{z_i^Tz_i-2\sum\limits_{n=1}\limits^{N}\lambda_n z_i^Tz_n+\sum\limits_{n=1}\limits^{N}\sum\limits_{m=1}\limits^{N}\lambda_n\lambda_m z_n^Tz_m}\\&=\sqrt{K(x_i,x_i)-2\sum\limits_{n=1}\limits^{N}\lambda_nK(x_i,x_n)+\sum\limits_{n=1}\limits^{N}\sum\limits_{m=1}\limits^{N}\lambda_n\lambda_mK(x_n,x_m)} \end{aligned}
R=∣∣zi−c∣∣=∣∣zi−n=1∑Nλnzn∣∣=ziTzi−2n=1∑NλnziTzn+n=1∑Nm=1∑NλnλmznTzm=K(xi,xi)−2n=1∑NλnK(xi,xn)+n=1∑Nm=1∑NλnλmK(xn,xm)
Hard-Margin versus Soft-Margin
11)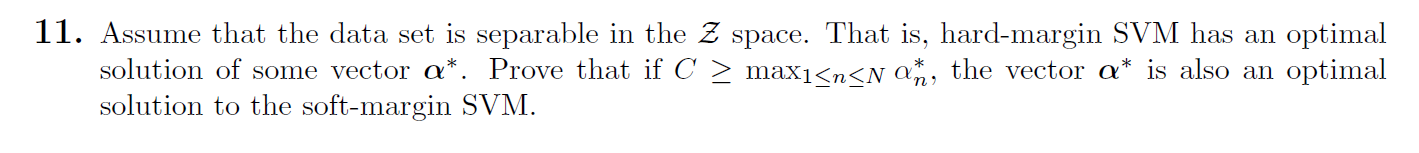

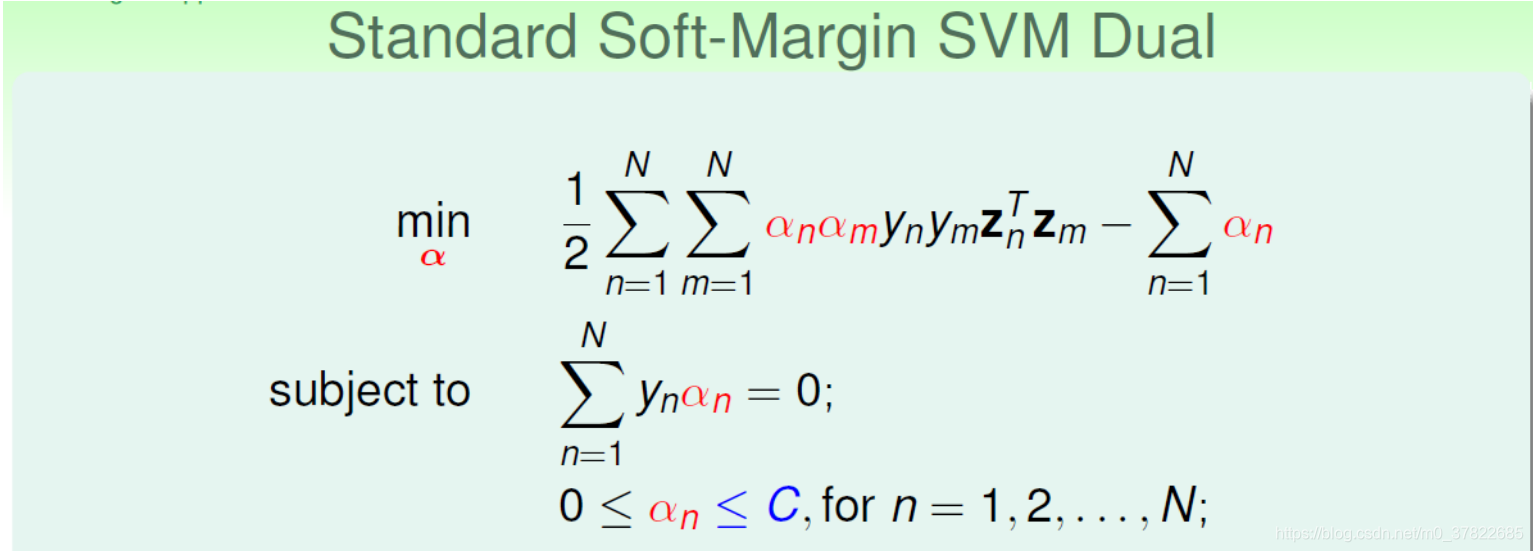
C
≥
max
1
≤
n
≤
N
α
n
∗
⟹
C
≥
α
n
∗
C\ge \max\limits_{1 \le n \le N}\alpha^*_n \implies C\ge \alpha^*_n
C≥1≤n≤Nmaxαn∗⟹C≥αn∗ for all $ n=1,\cdots,N$
由hard-margin和soft-margin svm对偶形式可知,若hard-margin SVM的一些最优解
α
∗
\alpha^*
α∗,若满足
α
∗
≤
C
\alpha^* \le C
α∗≤C,则这些
α
∗
\alpha^*
α∗同样为soft-margin svm的最优解。
Operation of Kernels
12)
C
~
\tilde{C}
C~时,最后的对偶形式只有约束条件发生变化
0
≤
α
n
≤
C
~
0 \le \alpha_n \le \tilde{C}
0≤αn≤C~
C
~
=
C
p
,
p
>
0
⟹
0
≤
p
α
n
≤
C
\tilde{C}=\frac{C}{p}, p>0 \implies 0 \le p\alpha_n \le C
C~=pC,p>0⟹0≤pαn≤C
min
α
1
2
∑
n
=
1
N
∑
m
=
1
N
α
n
α
m
y
n
y
m
z
n
T
z
m
−
∑
n
=
1
N
α
n
min
α
1
2
∑
n
=
1
N
∑
m
=
1
N
α
n
α
m
y
n
y
m
K
~
(
x
,
x
′
)
−
∑
n
=
1
N
α
n
min
α
1
2
∑
n
=
1
N
∑
m
=
1
N
α
n
α
m
y
n
y
m
p
K
(
x
,
x
′
)
−
∑
n
=
1
N
α
n
⟹
min
α
1
2
∑
n
=
1
N
∑
m
=
1
N
(
p
α
n
)
(
p
α
m
)
y
n
y
m
K
(
x
,
x
′
)
−
∑
n
=
1
N
(
p
α
n
)
\begin{aligned} &\min \limits_\alpha \frac12 \sum\limits_{n=1}\limits^{N} \sum\limits_{m=1}\limits^{N}\alpha_n\alpha_my_ny_mz_n^Tz_m-\sum\limits_{n=1}\limits^{N}\alpha_n \\ &\min \limits_\alpha \frac12 \sum\limits_{n=1}\limits^{N} \sum\limits_{m=1}\limits^{N}\alpha_n\alpha_my_ny_m\tilde{K}(x,x{'})-\sum\limits_{n=1}\limits^{N}\alpha_n \\ &\min \limits_\alpha \frac12 \sum\limits_{n=1}\limits^{N} \sum\limits_{m=1}\limits^{N}\alpha_n\alpha_my_ny_mpK(x,x{'})-\sum\limits_{n=1}\limits^{N}\alpha_n \\ &\implies \min \limits_\alpha \frac12 \sum\limits_{n=1}\limits^{N} \sum\limits_{m=1}\limits^{N}(p\alpha_n)(p\alpha_m)y_ny_mK(x,x{'})-\sum\limits_{n=1}\limits^{N}(p\alpha_n) \\ \end{aligned}
αmin21n=1∑Nm=1∑NαnαmynymznTzm−n=1∑Nαnαmin21n=1∑Nm=1∑NαnαmynymK~(x,x′)−n=1∑Nαnαmin21n=1∑Nm=1∑NαnαmynympK(x,x′)−n=1∑Nαn⟹αmin21n=1∑Nm=1∑N(pαn)(pαm)ynymK(x,x′)−n=1∑N(pαn)
通过解QP问题得到的
p
α
p\alpha
pα就与为
C
C
C时的
α
\alpha
α是一样的,接下来求
g
s
v
m
g_{svm}
gsvm。

b
=
y
s
−
∑
S
V
i
n
d
i
c
e
s
n
α
n
y
n
K
~
(
x
n
,
x
s
)
=
y
s
−
∑
S
V
i
n
d
i
c
e
s
n
(
p
α
n
)
y
n
K
(
x
n
,
x
s
)
b=y_s-\sum\limits_{SV indices n}\alpha_ny_n\tilde{K}(x_n,x_s)=y_s-\sum\limits_{SV indices n}(p\alpha_n)y_nK(x_n,x_s)
b=ys−SVindicesn∑αnynK~(xn,xs)=ys−SVindicesn∑(pαn)ynK(xn,xs)
g
s
v
m
(
x
)
=
s
i
g
n
(
∑
S
V
i
n
d
i
c
e
s
n
α
n
y
n
K
~
(
x
n
,
x
)
+
b
)
=
s
i
g
n
(
∑
S
V
i
n
d
i
c
e
s
n
(
p
α
n
)
y
n
K
(
x
n
,
x
)
+
b
)
g_{svm}(x)=sign(\sum\limits_{SV indices n}\alpha_ny_n\tilde{K}(x_n,x)+b)=sign(\sum\limits_{SV indices n}(p\alpha_n)y_nK(x_n,x)+b)
gsvm(x)=sign(SVindicesn∑αnynK~(xn,x)+b)=sign(SVindicesn∑(pαn)ynK(xn,x)+b)
所以是等价的。
Experiments with Soft-Margin Support Vector Machine

13)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
def get_dataset(file_name, n):
data_set = []
x = []
y = []
with open(file_name, "r") as f:
for line in f.readlines():
line = line.strip().split()
data_set.append(line)
f.close()
data_set = np.asarray(data_set, dtype=np.float64)
x = data_set[:, 1:]
y = data_set[:, 0]
for i in range(len(y)):
if (y[i] == n): y[i] = 1
else: y[i] = -1
return x, y
def save_parameter(content, filename):
file = open(filename, 'a')
for i in range(len(content)):
file.write(str(content[i])+'\n')
file.close()
def read_parameter(filename):
content = []
with open(filename, 'r') as f:
for line in f.readlines():
line = line.strip().strip('[').strip(']')
words = line.split(',')
content.append(words)
f.close()
#for i in range(len(content)):
return np.asarray(content, dtype=np.float64)
def err_rate(y_pred, y):
e_cnt = 0
n = len(y)
for i in range(n):
if (y_pred[i] != y[i]):
e_cnt += 1
return e_cnt / n
train_x, train_y = get_dataset("features.train.txt", 2)
test_x, test_y = get_dataset("features.test.txt", 2)
C_list = [1e-5, 1e-3, 1e-1, 1e1, 1e3]
# 前两列为w,最后一列为b
wb_list = []
for C in C_list:
clf = SVC(C=C, kernel='linear')
clf.fit(train_x, train_y)
w = clf.coef_[0].tolist()
b = clf.intercept_[0]
w.append(b)
wb_list.append(w)
log10_C = [-5, -3, -1, 1, 3]
w = wb[:, :2]
w_L2 = np.sqrt((w**2).sum(axis=1))
print(w_L2)
plt.plot(log10_C, w_L2)
plt.xlabel('$log_{10}C$')
plt.ylabel('$|w|$')
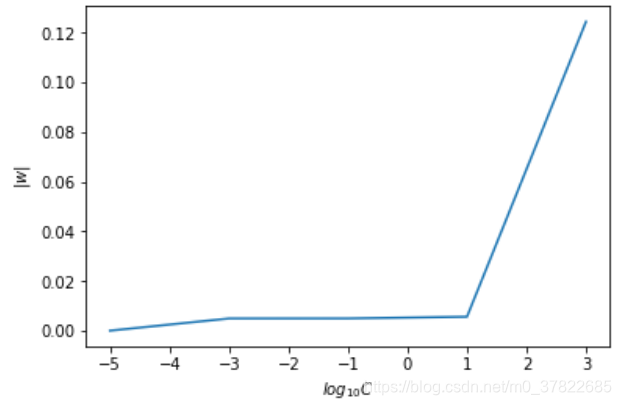
C越大w越大
14)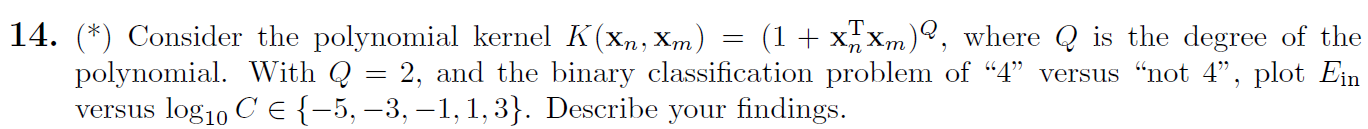
train_x, train_y = get_dataset('features.train.txt', 4)
test_x, test_y = get_dataset('features.test.txt', 4)
C_list = [1e-5, 1e-3, 1e-1, 1e1, 1e3]
e_in_list= []
for C in C_list:
clf = SVC(C=C, kernel='poly', degree=2, gamma=1, coef0=1)
clf.fit(train_x, train_y)
y_pred = clf.predict(train_x)
e_in_list.append(err_rate(y_pred, train_y))
log10_C = [-5, -3, -1, 1, 3]
plt.plot(log10_C, e_in_list)
plt.xlabel('$log_{10}C$')
plt.ylabel('$E_{in}$')
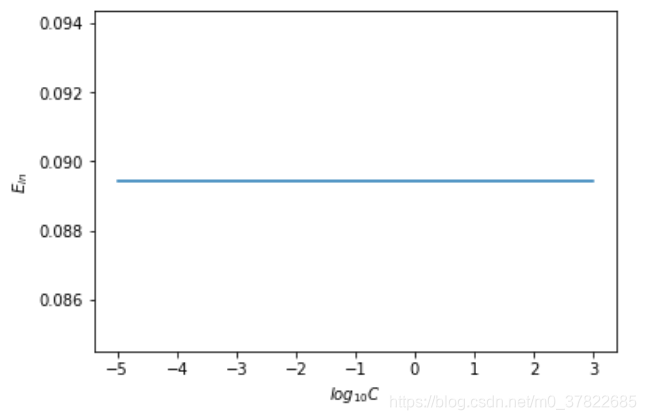
不同的C,
E
i
n
E_{in}
Ein是一样的
15)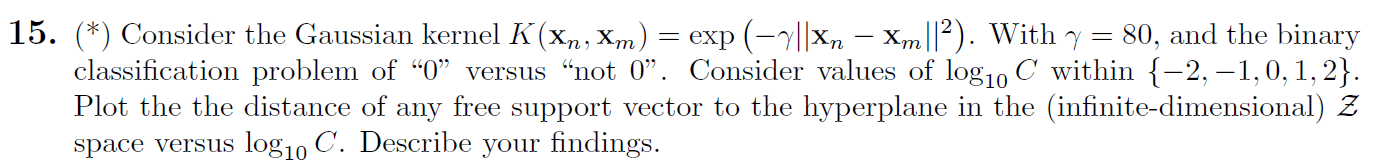
train_x, train_y = get_dataset('features.train.txt', 0)
test_x, test_y = get_dataset('features.test.txt', 0)
C_list = [1e-2, 1e-1, 1, 1e1, 1e2]
w_list = []
for C in C_list:
clf = SVC(C=C, kernel='rbf', gamma=80)
clf.fit(train_x, train_y)
y_alpha = clf.dual_coef_
m, n = y_alpha.shape
y_alpha = y_alpha.reshape(n, m)
sv = clf.support_vectors_
w = (y_alpha * sv).sum(axis=0)
w_list.append(w)
distance = 1 / np.sqrt((np.array(w_list) ** 2).sum(axis=1))
log10_C = [-2, -1, -0, 1, 2]
plt.plot(log10_C, distance)
plt.xlabel('$log_{10}C$')
plt.ylabel('distance')
C越大,支持向量离超平面越近,意味着对误差的容忍越小,就越‘硬’。
16)
def train_val_set():
train_x, train_y = get_dataset('features.train.txt', 0)
train_y = train_y.reshape(train_y.shape[0], 1)
data_set = np.concatenate((train_x, train_y), axis=1)
np.random.shuffle(data_set)
val_data = data_set[:1000]
train_data = data_set[1000:]
val_x = val_data[:, :2]
val_y = val_data[:, -1]
train_x = train_data[:, :2]
train_y = train_data[:, -1]
return train_x, train_y, val_x, val_y
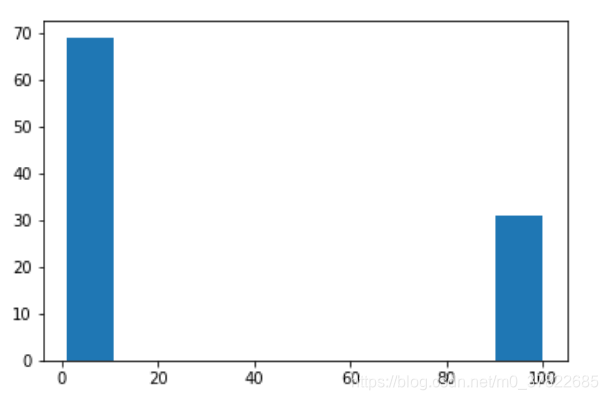
gamma_list = [1e-2, 1e-1, 1, 1e1, 1e2]
number = []
for i in range(100):
train_x, train_y, val_x, val_y = train_val_set()
err = []
for gamma in gamma_list:
clf = SVC(C=0.1, kernel='rbf', gamma=gamma)
clf.fit(train_x, train_y)
pred_y = clf.predict(val_x)
err.append(err_rate(pred_y, val_y))
index = err.index(min(err))
number.append(gamma_list[index])
plt.hist(number)





 本文深入探讨了机器学习中的多项关键技术,包括显式与隐式变换、核函数理论及其实验应用、支持向量机的硬间隔与软间隔概念、核函数操作以及软间隔支持向量机实验。通过对具体实例的解析,文章详细介绍了如何使用Python和scikit-learn库进行数据处理、模型训练和结果评估。
本文深入探讨了机器学习中的多项关键技术,包括显式与隐式变换、核函数理论及其实验应用、支持向量机的硬间隔与软间隔概念、核函数操作以及软间隔支持向量机实验。通过对具体实例的解析,文章详细介绍了如何使用Python和scikit-learn库进行数据处理、模型训练和结果评估。
















 2019
2019

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








