算法介绍
Floyd参考:这位作者的代码和公式已经非常棒了,所以对于过程和定义就不过多赘述了
排序法证明
其实上文链接也有证明过程,也有去翻过其他博客,基本都是这个证明过程,不过这个证明过程有些问题。
该证明过程的前提条件是点集内部是从小到大排序的,证明原理就是当求到k时,小于k的都已经得到最优解。
这样的证明限制了点集序号必须严格排序计算,但实际在计算过程中,点序是任意的,倒序、随机抽取都可,所以排序法的证明相对局限。
倒序: 6 5 4 3 2 1
奇偶互换:2 1 4 3 6 5
随机抽取:2 5 1 3 4 6
这里就不贴代码了,总之试过都AC了。
图解证明
由于各点之间没有顺序关系,为了避免误会,这里就不用1234…来标记了,直接用等价字母替代。
我们最终的目的是找一条最短路径,通往a->k:a->b->c->d->e->f->g->h->i->j->k,假设存在这么一条最短路径,即下图:

从a开始,经过许多点,最终到达k,此路径是最短的,故这里相邻两点之间肯定是互相连通着的。
很明显发现,比如a->c其代价很大:100,而a->b->c的代价很小:dis[a][b]+dis[b][c]=2,故最短路径走a->b->c。
1. 最优解集合的初始化
首先我们任意取一点:e
我们可以将e看作一个只包含自身的最优集合
我们不考虑其他点,只考虑e本身和其临近点,即:{d,e,f}

可以发现 能够得到 {d,e,f} 中任意两点间的最优解,即这个点集中互相到达情况下的最短路径。
以e为跳板,Floyd一定会遍历到:dis[d][f]=dis[d][e]+dis[e][f];而根据最短路径图可以得知,该路径值就是dis[d][f]的最优解。
故此时集合{d,e,f}内任意两点间的dis都是最优的.
此时是以e为选中点,将其左右临近点纳入自身的最优集合之中
2. 最优解集合的扩大

我们紧接着再假设下一个选取的点为:f
我们可以发现在 {d、e、f}点集中,以f为选中点,可以与临近点g取得联系。
例如dis[d][g]=dis[d][f]+dis[f][g],从d->g的路线即d->e->f->g。
我们不考虑其他点,只考虑集合 {d、e、f}和临近点g,Floyd算法会将任意两点间以f为跳板,计算出其中最短的路径,最终在这个{d,e,f,g}点集中,任意两点都是最短路径。
此时我们是以f为选中点,将右边的临近点g纳入集合(左边的临近点已经是最优集合内的点)。

3. 最优解集合的合并
由于是随机选择,出现下面情况的可能性也是非常大的。
我们依次选择了e,f,i,h作为选中点,最后发现存在两个最优解集合{d,e,f,g}、{g,h,i,j}。

此时我们以g为选中点,可以发现,两边集合都可以通过g作为跳板,例如可推出最优距离dis[d][i]=dis[d][g]+dis[g][i]。
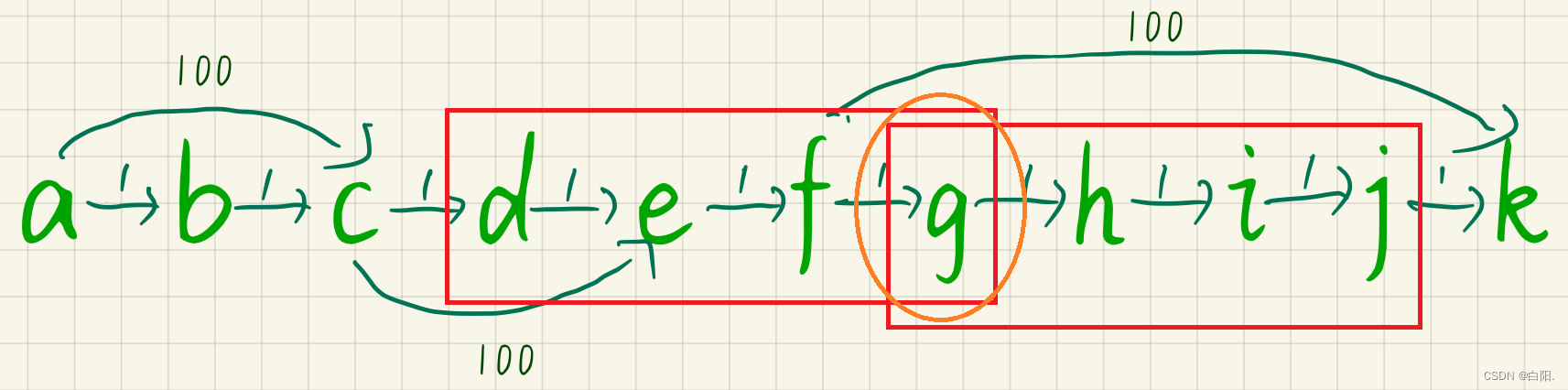
在这个{d,e,f,g,h,i,j}的集合中,经过Floyd的遍历,该集合以g为跳板,最终形成集合内最优解,集合内任意两点之间的dis都是最优的。
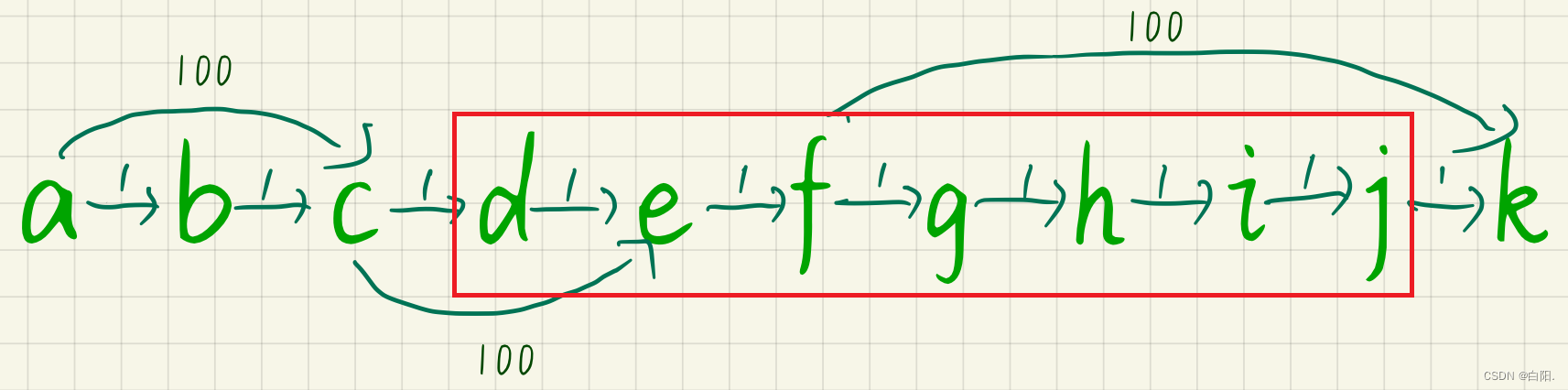
此时我们是以g为选中点,因左右两边都是集合,故发生合并。
4. 全集最优解
依据上述步骤,每一个点都会被选择一次,最优解集合会不断地扩张,最终整个点集都纳入最优解集合。




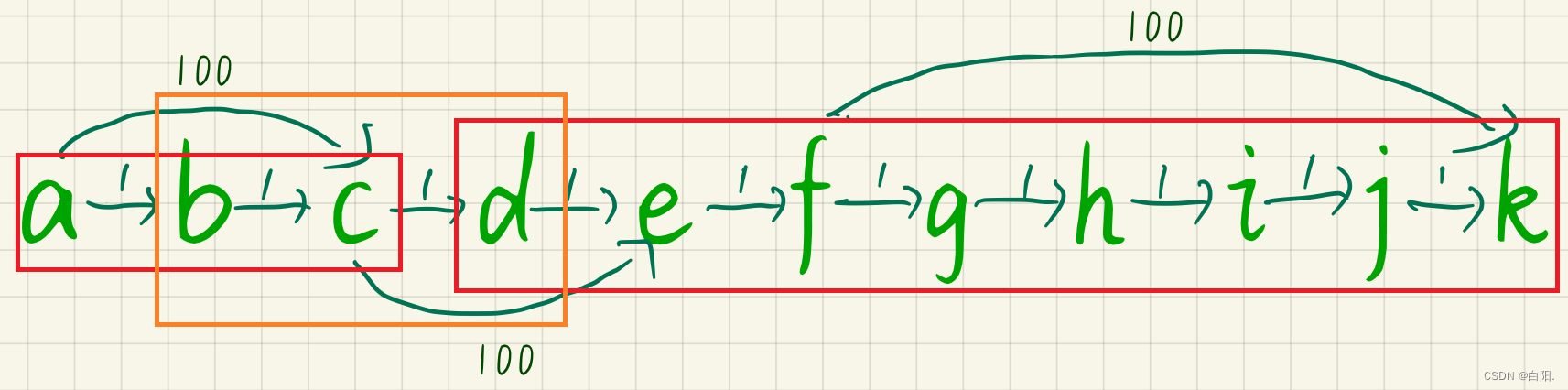



a->k得到了最优解:a->b->c->d->e->f->g->h->i->j->k。
总结:选择任意点集(单独一个点也是一个点集),其可以吸纳融合临近的点集。故通过不断地选择任意点集,局部的点集合不断吸纳融合扩大,最终得到全局合并的最优集合。








 本文详细解析了Floyd-Warshall算法的排序法证明存在的局限,并通过图解方式深入阐述了算法如何逐步找到点集间的最短路径。通过实例展示了算法在不同点序下的适用性,证明了算法的普适性,最终得出通过不断选择点集并融合临近点集,可以找到全局最优解的结论。
本文详细解析了Floyd-Warshall算法的排序法证明存在的局限,并通过图解方式深入阐述了算法如何逐步找到点集间的最短路径。通过实例展示了算法在不同点序下的适用性,证明了算法的普适性,最终得出通过不断选择点集并融合临近点集,可以找到全局最优解的结论。
















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








