吴恩达《Machine Learning》-Neural Networks Learning神经网络学习（九）

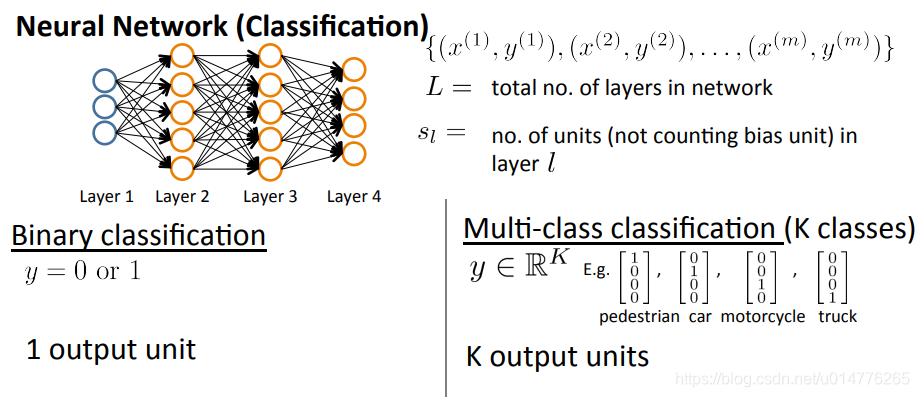
L表示神经网络有多少层，本例中为4层L=4
st表示神经网络一层中有多少个神经节点，s1=3，s2，s3=5，s4=4
对于单分类问题，sL=1（sL也就是最后一层输出层）
对于多分类问题，sL=k（k>=3）k表示结果输出多少类别。若k<3，则输出为1类，剩下的另一类采用全集-当前类即可。

损失函数cost function：

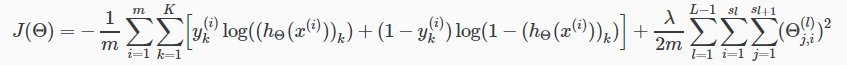
最后输出多少类，k等于多少。
对于正则项，不加入bias unit偏置单元,也就是i=0的项我们不加入其中。
在正则化部分，我们必须考虑多个θ矩阵。当前theta矩阵中的列数等于当前层中的节点数（包括偏移单位）。当前theta矩阵中的行数等于下一层中的节点数（不包括偏移单位）。

例如：

第二个参数Θ：Θi0（2）*x0+Θi1（2）*x1

练习题：

选择（D），优化函数一般需要提供J（Θ）和Θ的偏导数

Backpropagation Algorithm反向传播算法

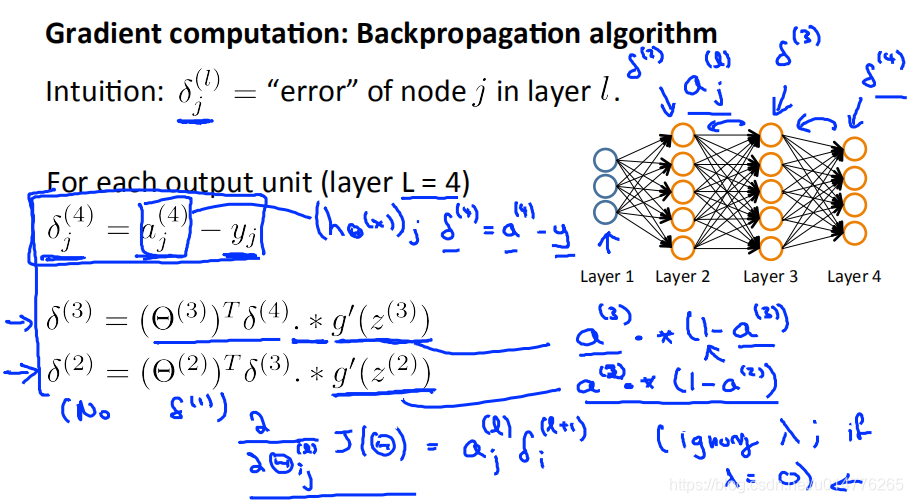
δ（4）=aj（4）-yj （aj（4）=（hθ（x））j）
换成向量表达：δ（4）=a（4）-y

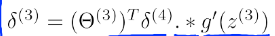
其中.*表示矩阵元素对应相乘（哈达马积（Hadamard product））
g’（z（3））表示g的导数

偏导数

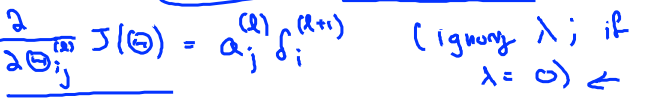
不包含正则项，假如λ=0，忽略λ.

首先正向计算每一个a（l），之后使用δ（L）=a（L）-y（i）反向计算 δ（L）

练习题：

选择（D）

向前传播：

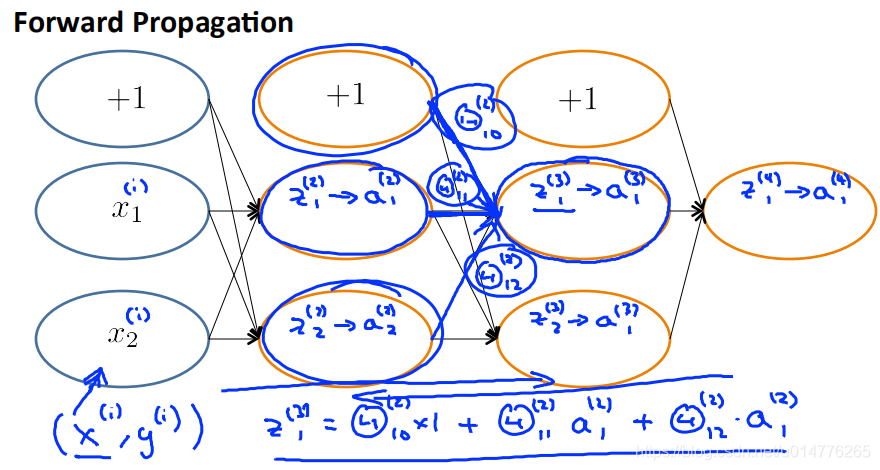
反向传播算法解析：

前面连接节点的δ值乘上连接线的Θ值
δ2（2）=Θ12（2）*δ1（3）+Θ22（2）*δ2（3）
δj（l）的偏导数

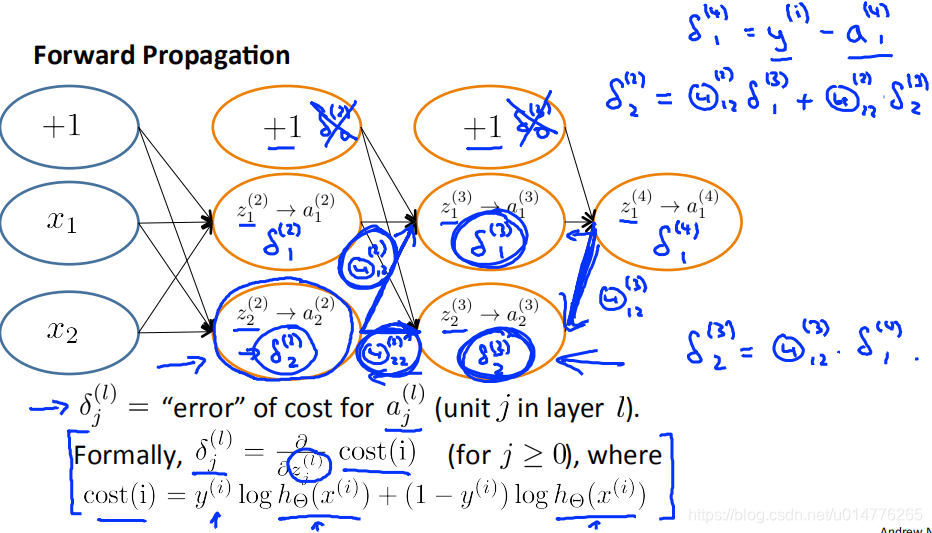
练习题：

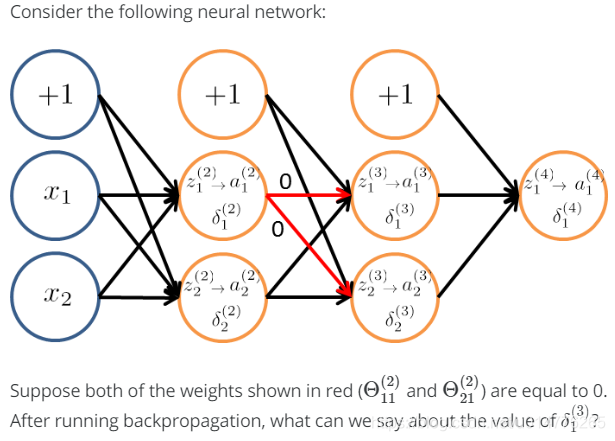
选择（D），只能去判断δ1（2）为0，前面的节点无法判断

实施笔记：将参数展开 Implementation Note: Unrolling Parameters

原来的损失函数的theta，gradient都是n+1维向量。可是到了神经网络中，其变成了矩阵。故想要使用原来的损失函数的方法，需要将矩阵展开成向量。

将矩阵转化为向量代码：

将向量转化为矩阵代码：

练习题：

选择（C）
将D1转成向量[0 0 0 0] 为1行60列
将D2转成向量 [0 0 0 0] 为1行11列
故选择D2是从61到71（注意61到71为11个数字）

使用向量传入损失函数计算，并返回向量。（需要将向量转化为矩阵）

Gradient Checking梯度检查

由于反向传播计算偏导数实施很复杂，传统方法的优化函数，如：梯度下降法。可以被证明出可能会产生计算错误。所以对于反向传播问题，我们使用Gradient Checking梯度检查来确保导数计算正确。

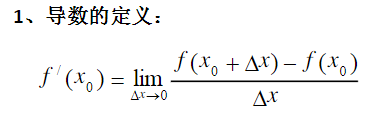
公式推导（我自己写的,不一定对）：

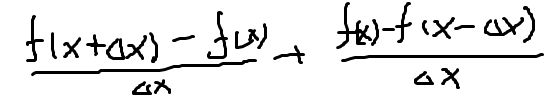
计算公式：

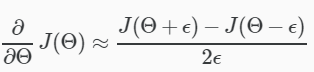
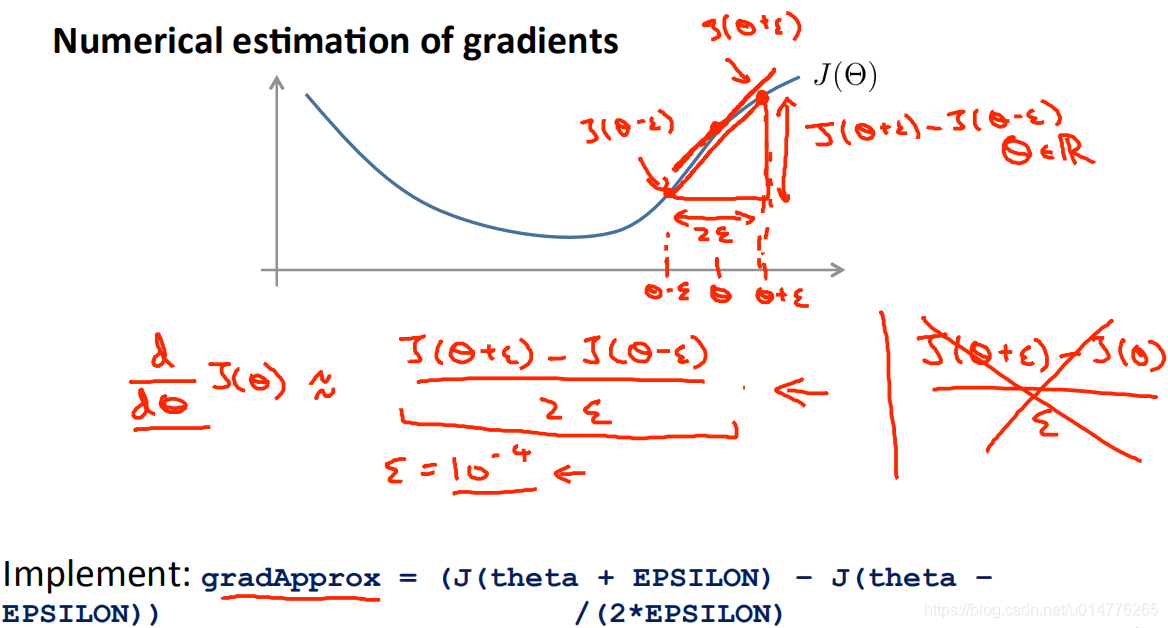
练习题：

选择（B）
(1.01)³-(0.99)³/0.02=1.030301-0.970299/0.02=3.0001

θ参数的偏导数

使用octave代码实施：

如果反向传播的偏导数结果：DVec约等于grandApprox（Gradient Checking梯度检查计算的偏导数），则认为结果正确。

1.首先使用反向传播计算偏导数：DVec
2.使用数值梯度检查 计算：grandApprox
3.保证两个值 之间有相似数值
4.如果数值相似，关闭数值梯度检查。使用反向传播计算偏导数的结果。（因为数值梯度检查十分占用计算能力）

练习题：

选择（B），数值梯度检查十分占用计算资源

Random Initialization随机初始化

如果对于逻辑回归，线性回归等算法，将Θ初始值设置为0矩阵是正确的。但是对于神经网络来说，Θ初始值设置为0矩阵是错误的。

the problem of symmetric ways对称方法问题

Random Initialization随机初始化是为了解决对称方法产生的问题。
如果采用0矩阵，同一组输入节点的参数会相同，导致后面节点的数值也相同。a1（2）=a2（2）。这样到后面隐含层中，两个节点的就相当于一个节点了。

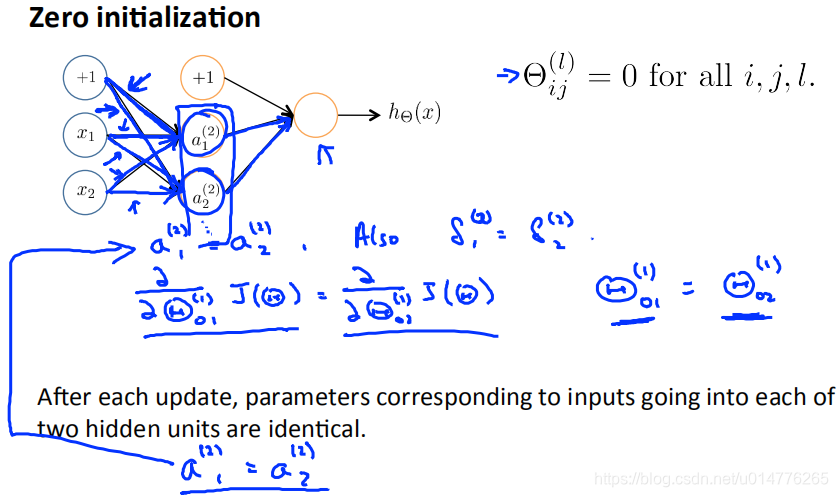
Symmetry breaking对称打破

所有随机矩阵random matrix数值区间在[0,1]之间。故经过随机初始化，数值分布在[-ε，ε]区间。
举例：
若ε=0时，0*（2ε）-ε =-ε
若ε=1时，1（2*ε）-ε =ε

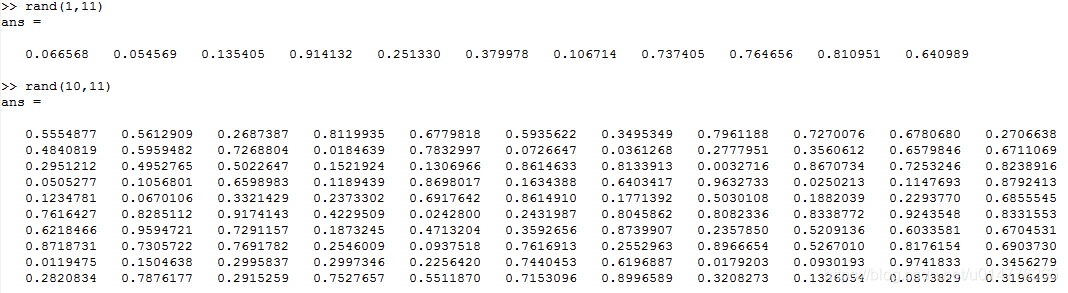
练习题：

选择（D），并没有打破对称。一行一列的随机矩阵，相当于一个数字。

神经网络总结：

1.首选选择网络结构
确定输入的特征数
确定输出的类别数
确定有几层隐含层和一层隐含层中有多少隐藏节点。（如果有多个隐藏层，建议在每个隐藏层中使用相同数量的隐藏节点。）

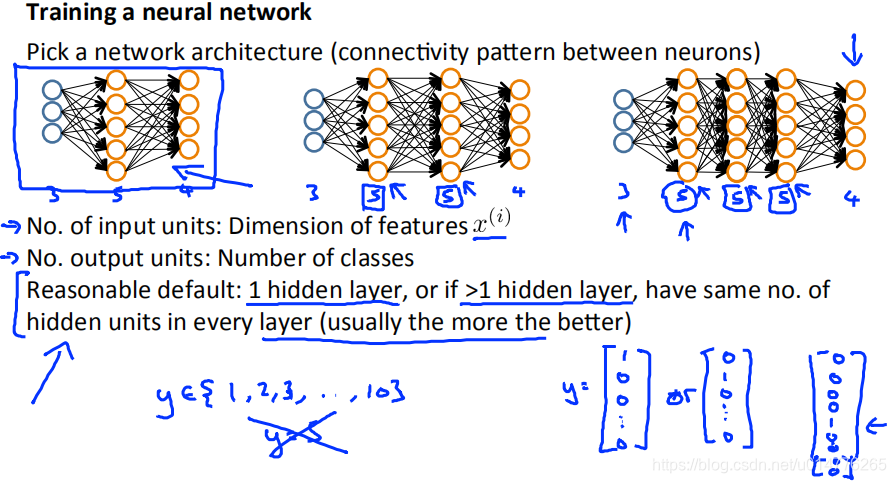
训练神经网络步骤：

画出Θ和J（Θ）的图像。低点为局部最优点，其值约等于真实值。
高点与真实值差距很大。

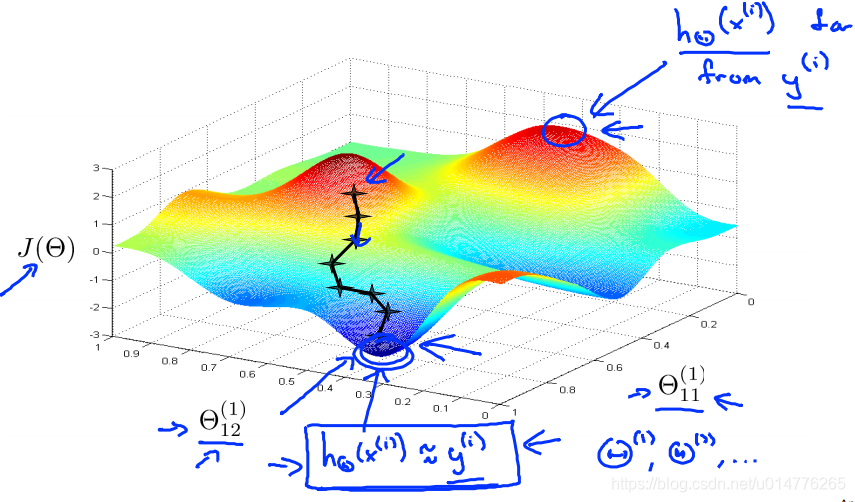
练习题：

选择（C），保证每一轮迭代中J（Θ）都在下降

测试题：

选择（B）
解析：


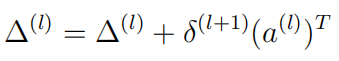
选择（A）

选择（A）

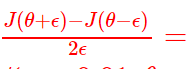
2*(θ+ϵ)⁴+2-2*(θ-ϵ)⁴+2/2ϵ=(θ+ϵ)⁴-(θ-ϵ)⁴/ϵ
将ϵ=0.01, θ=1 代入上式,并化简一下可得出
(1+0.01)⁴-(1-0.01)⁴/0.01=1.04060401-0.96059601/0.01=8.0008

选择（B,D）
A.以前的quiz中遇到过,当选的λ太大时,会成为一条直线,underfit. 不正确
B.Gradient checking就是用来验检神经网络内部的计算结果对不对的. 正确 **
C.Gradient checking是验检神经网络内部的计算结果对不对,不关心是用的哪个算法,高级算法如fminuc与原始的sigmoid梯度下降都可以用gradient checking来验检. 不正确
D.正确。如果神经网络已经对于数据集过拟合，那么增加正则项参数λ.，可以避免过拟合。

选择（A，B）
B.使用随机初始化，由于初值不同可能导致下降方向不同。最后下降到不同的最优点。