区间dp-凸多边形最优三角剖分

最新推荐文章于 2021-10-14 16:34:44 发布

H_ang

最新推荐文章于 2021-10-14 16:34:44 发布

阅读量334

点赞数

CC 4.0 BY-SA版权

分类专栏：区间dp

本文链接：https://blog.youkuaiyun.com/qq_21433411/article/details/94390892

区间dp 专栏收录该内容

17 篇文章

订阅专栏

本文介绍了一种求解最优三角剖分问题的算法，并通过动态规划方法进行实现。算法首先初始化所有可能的子问题解，然后通过枚举区间的长度、起点和分割点来寻找最优解。最后，通过递归函数输出最优的三角剖分方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

转一篇博客：https://blog.youkuaiyun.com/pi9nc/article/details/9750091
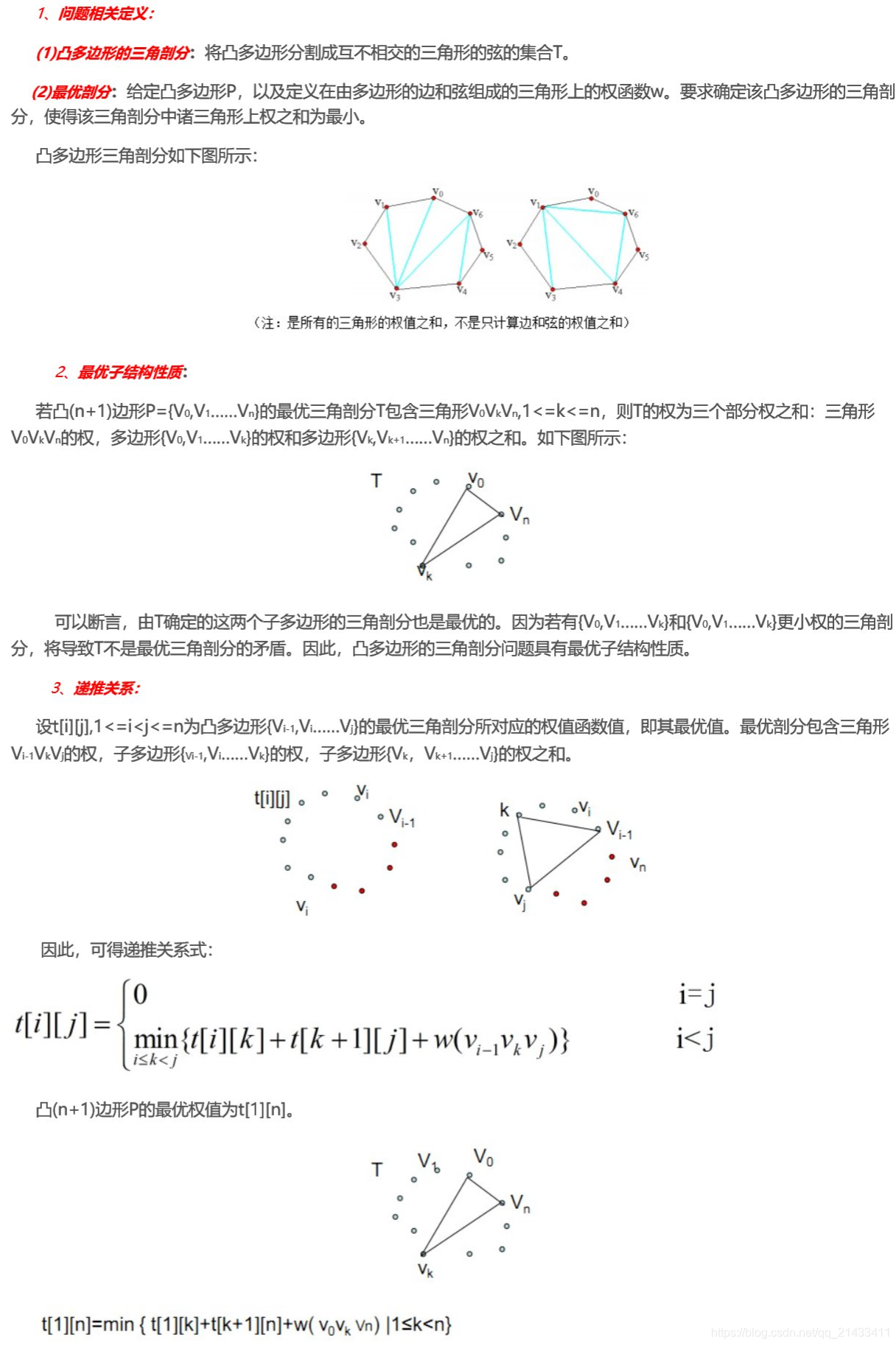
在这里插入图片描述

我的代码改了一下：dp[i][j]表示从i到j的最优三角剖分。

好像最优三角剖分和表达式树有关系。留坑。

#include <bits/stdc++.h>
using namespace std;

int w[10][10];
int dp[10][10];
int s[10][10];
int dfs(int n)
{
    for(int i=1;i<=n;i++)
    {
        dp[i][i+1]=0;
    }
    for(int Len=2;Len<=n-1;Len++)//枚举区间长度
    {
        for(int L=1;L+Len<=n;L++)//枚举起点
        {
            int R=L+Len;//计算终点
            dp[L][R]=10000000;
            for(int k=L+1; k<R; k++)//枚举分割点
            {
                int u=dp[L][k]+dp[k][R]+w[L][k]+w[L][R]+w[k][R];
                if(u<dp[L][R])
                {
                    dp[L][R]=u;
                    s[L][R]=k;//记录最优分割点
                }
            }
        }
    }
    return dp[1][n];
}

void put(int L, int R)//输出最优三角剖分
{
    if(R-L<=1)
    {
        return;
    }
    printf("V%d V%d V%d\n",L, R, s[L][R]);
    put(L, s[L][R]);
    put(s[L][R], R);
}

int main()
{
    int n;
    scanf("%d",&n);
    memset(dp, 0, sizeof(dp));
    memset(w, 0, sizeof(w));
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            scanf("%d",&w[i][j]);
        }
    }
    cout<<dfs(n)<<endl;
    put(1, n);

    return 0;
}
/*

6
0 2 2 3 1 4
2 0 1 5 2 3
2 1 0 2 1 4
3 5 2 0 6 2
1 2 1 6 0 1
4 3 4 2 1 0

*/