区间dp-LightOJ-1422-万圣节服装_c++ 万圣节服饰-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_21433411/article/details/94393452

本文探讨了一个关于宴会礼服选择的优化问题，通过区间动态规划算法寻找参加连续宴会所需的最少礼服数量，详细解析了算法思路及实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接：https://vjudge.net/contest/308310#problem/B
题目大意：有N个宴会，对于每一个宴会，女主角都要穿一种礼服，礼服可以套着穿，但是脱了的不能再用，参加宴会必须按顺序来，从第一个到第N个，问参加这些宴会最少需要几件礼服。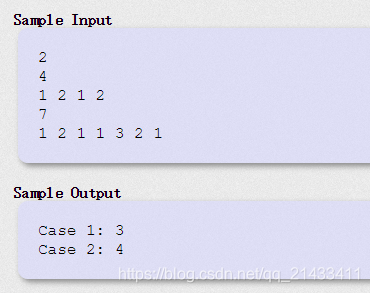在这里插入图片描述
样例一解释：第一天穿1号衣服，第二天套2号衣服。第三天把2号衣服脱了。第四天再穿一件2号衣服。
因为脱了的衣服不能在穿，所以需要两件2号衣服，一件1号衣服。

区间dp：

对于第[i, j]天需要最少的衣服为dp[i][j]

第j天的衣服有两种来源：在[i, j]穿过了。新穿的。

新穿的:dp[i][j]=dp[i][j-1]+1
在[i, j]穿过了:枚举[i, j]与第j天衣服相同的天k。
那么dp[i][j]=dp[i][k]+dp[k+1][j-1]：[k+1, j-1]的衣服全部要脱下

#include <bits/stdc++.h>
using namespace std;

int a[105];
int dp[105][105];
int n;

int dfs()
{
    for(int Len=2;Len<=n;Len++)//区间长度
    {
        for(int L=1;L+Len-1<=n;L++)//起点
        {
            int R=L+Len-1;//终点
            //第R天的衣服是新穿的
            dp[L][R]=dp[L][R-1]+1;
            for(int k=L;k<R;k++)
            {
                if(a[k]==a[R])
                {
                    //是[L, R]中有一天穿的，那么要把[K+1, R-1]的衣服脱完
                    dp[L][R]=min(dp[L][R], dp[L][k]+dp[k+1][R-1]);
                }
            }
        }
    }

    return dp[1][n];
}

int main()
{
    int CUT=1;
    int t;
    scanf("%d",&t);
    while(t--)
    {
        memset(dp, 0, sizeof(dp));
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            dp[i][i]=1;
        }
        printf("Case %d: %d\n", CUT++, dfs());
    }


    return 0;
}