语音识别 CTC Loss

(以下内容搬运自 PaddleSpeech)

Derivative of CTC Loss

关于CTC的介绍已经有很多不错的教程了，但是完整的描述CTCLoss的前向和反向过程的很少，而且有些公式推导省略和错误。本文主要关注CTC Loss的梯度是如何计算的，关于CTC的介绍这里不做过多赘述，具体参看文末参考。

CTC主要应用于语音和OCR中，已语音Deepspeech2模型为例，CTC的网络一般如下图所示，包含softmax和CTCLoss两部分。反向传播需要求得loss L相对于logits $u^i$​的梯度。下面先介绍CTCLoss的前向计算。

图片来源于文末参考

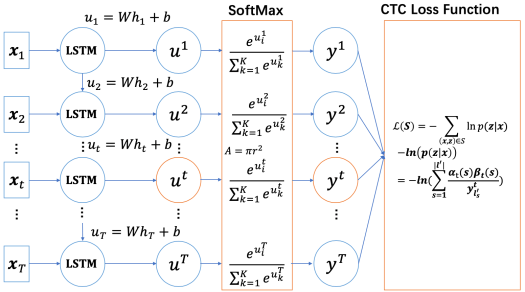
CTC Loss 的计算

CTC中path的定义与概率的计算如下：

path 是 $ L’^T$​​的元素，用 $\pi$​​表示。 $\text{x}$​​ 是输入特征，$\text{y}$​​ 是输出label， 都是序列。 $L$​​ 是输出的 vocab, L‘ 是 $L\cup blank$​​。 $y_{{\pi }_t}^t$​​ 表示在t时刻，${\pi }_t$​​ label时的观察概率。其中${\pi }_t$​​ 表示 $\pi$​​ path在t时刻的label。$\pi$​​ 是 $\text{y}$​​ 与 $\text{x}$​​ 的一个alignment，长度是$T$​​，取值空间为$L^{\prime }$​​​。path也称为alignment。

公式（2）解释了给定输入 $\text{x}$​ ，输出 $\pi$​ path 的概率，即从时间t=1到T每个时间点的概率 $y_{{\pi }_t}^t$​ 相乘。

求出单条path后，就可以计算$p(l\mid x)$​ 的概率，计算如下：

这里边 $\mathcal{B}$ 就是映射， 即所有多对一的映射（many-to-one mapping )的集合。 这样就算出来对应一个真正的 label $\text{l}$ 的概率了，这里是求和。 求和的原因就是 aab 和 abb 都是对应成ab, 所以 aab 的概率 + abb 的概率才是生成ab的概率。

公式（3）解释了给定输入 $\mathbf{x}$​​​​​​ ，求输出$\mathbf{l}$​​​​​​ 的概率， 即所有集合 ${\mathcal{B}}^{-1}(\mathbf{l})$​​​​​​​​​​ 中 path的概率和。

CTC forward-backward 算法

CTC的优化采用算最大似然估计MLE (maximum likelihood estimation), 这个和神经网络本身的训练过程是一致的。

这个CTC 计算过程类似HMM的 forward-backward algorithm，下面就是这个算法的推导过程：

上图中的定义很清楚， 但是${\alpha }_{t-1}(s)$ and ${\alpha }_{t-1}(s-1)$ 和 ${\alpha }_t(s)$ 的关系也不那么好看出来，下图给出了具体的关于 ${\alpha }_t(s)$ 的推导过程：

这里的公式比较适合用下面的图来理解，${\alpha }_1(1)$​​​​ 其实对应的就是下图中左上角白色的圆圈。 就是上来第一个是blank 的概率， 而 ${\alpha }_1(2)$​​​​是label l 的第一个字母。 这里边我们假设每个字母之间都插入了空白，即label l扩展成l’，例如，l=[a, b, b, c]， l’=[-, a, -, b, -, b, -, c, -]。 然后对于其他圆点，在时间是1 的情况下概率都是 0. Figure 3中横轴是时间 t，从左到右是1到T；纵轴是s（sequence），从上到下是 1 到 $\mid {\mathbf{l}}^{\prime }\mid$​​​​.

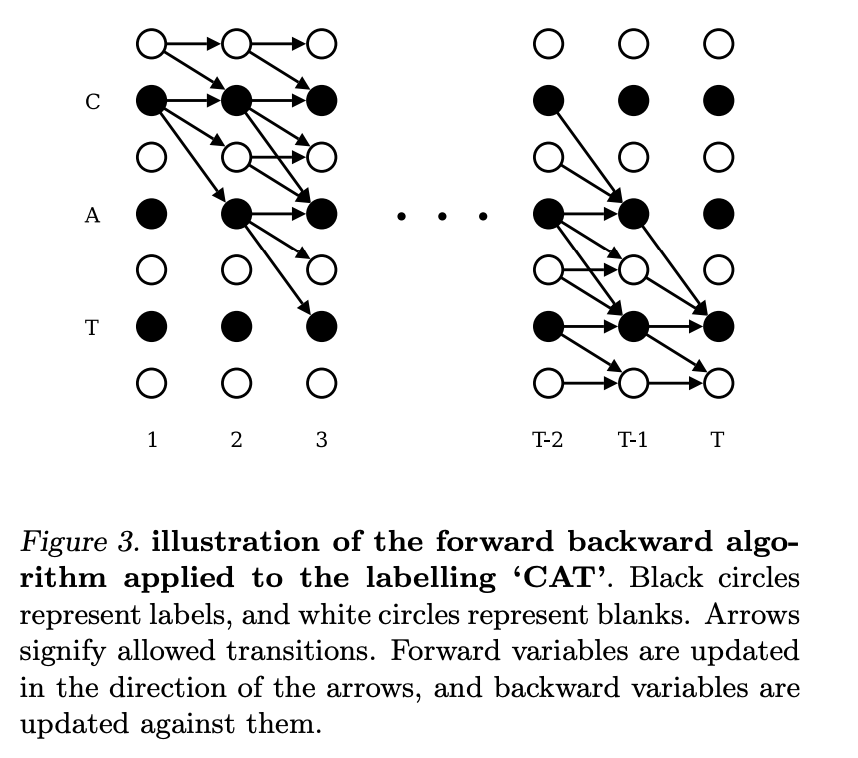
接下来我们分析递归公式 (resursion)，更多介绍可以参看 [2]. 公式6分情况考虑:

• 第一种情况就是当前的label是blank， 或者 ${{\mathbf{l}}^{\prime }}_s={{\mathbf{l}}^{\prime }}_{s-2}$​​​​​​​(相邻是重复字符)：

这个时候他的概率来自于过去t-1的两个label 概率， 也就是 $a_{t-1}(s)$​​ 和 $a_{t-1}(s-1)$​​​ 。

$a_{t-1}(s)$​​ 就是说当前的 sequence 已经是 s 了，figure 3中表现为横跳， blank -->blank（例如t=3, s=3）；

而 $a_{t-1}(s-1)$是说明当前的字符还不够， 需要再加一个， 所以在figure 3中就是斜跳，从黑色圆圈到白色圆圈（例如，t=3, s=5）。

仔细观察figure 3， 除了第一排的白色圆圈， 其他白色圆圈都有两个输入， 就是上述的两种情况。 当然判断blank 的方法也可以是判断$I_{s-2}^{\prime }=I_s^{\prime }$​. 这种情况也是说明$I_s^{\prime }$​​​ 是blank, 因为每一个字符必须用 blank 隔开， 即使是相同字符。

• 第二章情况 也可以用类似逻辑得出， 只不过当前的状态s 是黑色圆圈， 有三种情况输入。

最终的概率就如公式8 所示， 这个计算过程就是 CTC forward algroirthm， 基于 Fig. 3 的左边的初始条件。

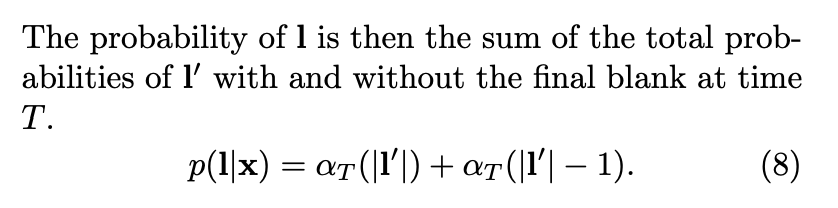
基于Fig. 3 右边的初始条件，我们还是可以计算出一个概率， 那个就是 CTC backward. 这里我就不详细介绍了， 直接截图。

这样一直做乘法， 数字值越来越小，很快就会underflow。 这个时候就需要做 scaling.

算出了forward probability 和 backward probability 有什么用呢， 解释如下图。

上图是说 forward probability and backward probability 的乘积， 代表了这个 sequence $\mathbf{l}$ t时刻，是s label 的 所有paths 的概率。 这样的话 我们就计算了 Fig. 3 中的每个圆圈的概率。为什么${\alpha }_t(s){\beta }_t(s)$ 中多出一个 $y_{{\mathbf{l}}_{\mathbf{s}}^{\prime }}^t$ ，这是因为它在 $\alpha$ 和 $\beta$ 中都包含该项，合并公式后就多出一项。

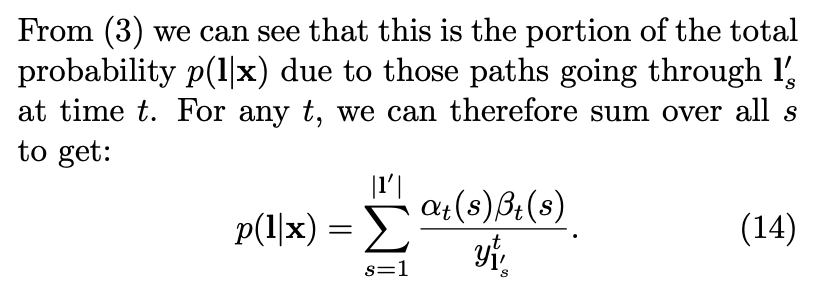
$p(\mathbf{l}|\mathbf{x})$​ 可以通过任意时刻 t 的所有 s 的 foward-backward 概率计算得来。取负对数后就是单个样本的NLL（Negative Log Likelihood）。

总结

总结一下，根据前向概率计算CTCLoss函数，可以得出如下结论：

1. 对于时序长度为T的输入序列x和输出序列z，前向概率：
   $$\begin{array}{rl}{\alpha }_t(s)& =\sum _{\underset{{\pi }_t=l_s^{\prime }}{\pi \in {\mathcal{B}}^{-1}(z)}}p({\pi }_{1:t}|x)\\ {\alpha }_1(1)& =y_{-}^1;{\alpha }_1(2)=y_{l_2^{\prime }}^1,{\alpha }_1(s)=0,\forall s>2\\ {\alpha }_t(s)& =0,\forall s<|l^{\prime }|-2(T-t)-1,\text{or}\forall s<1\\ {\alpha }_t(s)& =\{\begin{array}{ll}({\alpha }_{t-1}(s)+{\alpha }_{t-1}(s-1))y_{l_s^{\prime }}^t& \text{if ls′=b or ls−2′=ls′}\\ ({\alpha }_{t-1}(s)+{\alpha }_{t-1}(s-1)+{\alpha }_{t-1}(s-2))y_{l_s^{\prime }}^t& \text{otherwise}\end{array}\end{array}$$

2. 利用 ${\alpha }_t(s)$ 计算CTCLoss：
   $$-ln(p(l\mid x))=-ln({\alpha }_T(|l^{\prime }|)+{\alpha }_T(|l^{\prime }|-1))$$

根据后向概率计算CTCLoss函数，可以得出如下结论：

1. 对于时序长度为T的输入序列x和输出序列z，后向概率：
   $$\begin{array}{rl}{\beta }_t(s)& =\sum _{\underset{{\pi }_t=l_s^{\prime }}{\pi \in {\mathcal{B}}^{-1}(z)}}p({\pi }_{t:T}|x)\\ {\beta }_T(|l^{\prime }|)& =y_{-}^T;{\beta }_T(|l^{\prime }|-1)=y_{l_{|l^{\prime }|-1}^{\prime }}^T,\\ {\beta }_t(s)& \\ {\beta }_t(s)& \end{array}$$