全文概要
SQ 是一种增量量化的方法,其大概思路和 INQ 一样,选择部分参数进行量化,其他保持全精度。即该方法只针对权重进行。
SQ 通过给定的一系列量化比例 r,选择一层中的 r 比例卷积核进行量化。衡量每个卷积核的量化误差,依据量化误差得到该卷积核被选为量化卷积核的概率(虽然最后发现均匀概率函数效果最好)。通过逐渐增加 r 的大小(从50%→75%→87.5%→100%50\%\rightarrow75\%\rightarrow87.5\%\rightarrow100\%50%→75%→87.5%→100%),达到增量量化的效果。
作者认为,量化误差大的卷积核和量化误差小的,其理想的优化梯度方向不同。因此分开来量化可能会带来好结果。
简介
作者认为,之前的量化方法存在两个问题:
- 量化只针对分类任务,对检测任务、分割任务缺少灵活性;
- 在 low-bit 空间,难以实现 full-precision 空间的局部最小值无损迁移到 low-bit 空间的局部最小值;
本文还讨论了 SQ 方法影响量化的四个问题:
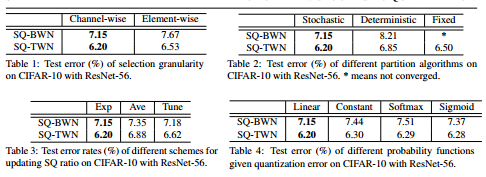
- 粒度:是以权重卷积核为单位,还是以权重元素为单位;以卷积核的粒度进行分组量化比较合适,因为作者认为一个卷积核是由卷积元素相互影响的结构组成;
- 选择算法:是确定性算法(按概率排序),还是随机性算法;随机性算法能更好地“探索”,采用轮盘赌算法;
- 量化概率:基于量化误差,如何选择量化概率函数;实验结果表明,线性函数能达到更好的结果;pi=fi∑j(fj)p_i=\frac{f_i}{\sum_j(f_j)}pi=∑j(fj)fi
- SQ更新方案:选择适当的方案来更新 SQ 比率;作者尝试了20%→40%→60%→80%→100%20\%\rightarrow40\%\rightarrow60\%\rightarrow80\%\rightarrow100\%20%→40%→60%→80%→100%的SQ组合以及50%→75%→87.5%→100%50\%\rightarrow75\%\rightarrow87.5\%\rightarrow100\%50%→75%→87.5%→100%的组合,发现后者表现更好,作者给后者取名为指数更新方案;
SQ方法介绍
量化误差衡量:ei=∥Wi−Qi∥1∥Wi∥1e_i=\frac{\|W_i-Q_i\|_1}{\|W_i\|_1}ei=∥Wi∥1∥Wi−Qi∥1
中间变量,反应量化误差和被选择概率的反比例关系:fi=1ei+ϵf_i=\frac1{e_i+\epsilon}fi=ei+ϵ1 其中ϵ\epsilonϵ是个很小的数,比如10−710^{-7}10−7
概率函数有四种考虑:
- 常数函数:pi=1mp_i=\frac1mpi=m1
- 线性函数:pi=fi∑jfjp_i=\frac{f_i}{\sum_jf_j}pi=∑jfjfi
- Softmax函数:pi=exp(fi)∑jexp(fi)p_i=\frac{exp(f_i)}{\sum_jexp(f_i)}pi=∑jexp(fi)exp(fi)
- Sigmoid函数:pi=11+exp(−fi)p_i=\frac1{1+exp(-f_i)}pi=1+exp(−fi)1
在训练时,混合使用量化权重和全精度权重,反向传播正常进行;
实验细节
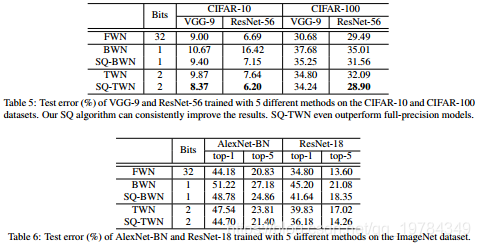
数据集 CIFAR-10 和 CIFAR-100。对于前面一个数据集使用两个网络 VGG-9 和 ResNet-56。对于 VGG-9,solver 参数设置如下:SGD,动量设为0.90.90.9;权重衰减设为0.00010.00010.0001;batch size设为100100100;初始学习率设为0.10.10.1,每15k15k15k个迭代除以101010;一共训练100k100k100k次迭代。对于ResNet-56,参数设置和残差网络出来的那篇论文一样;
数据集 ImageNet,使用两个网络: AlexNet-BN 和 ResNet-18。对于 AlexNet-BN,参数设置为:SGD,动量设为0.90.90.9,权重衰减设为5∗10−55*10^{-5}5∗10−5,batch size 设为256256256;初始学习率设为0.010.010.01,分别在100k、150k、180k100k、150k、180k100k、150k、180k次迭代除以101010;一共训练200k200k200k次迭代。对于 ResNet-18,参数设置为:SGD,batch size 设为100100100,权重衰减5∗10−55*10^{-5}5∗10−5,动量设为0.90.90.9;初始学习率设为0.050.050.05,当出现误差平原(error plateaus)就除以101010;一共训练300k300k300k次迭代。
SQ 方法默认设置为:channel-wise的粒度;划分方式为随机划分(轮盘赌算法);量化概率函数为线性函数;SQ更新方案为50% →\rightarrow→ 75% →\rightarrow→ 87.5% →\rightarrow→ 100%。








 SQ是一种用于神经网络权重增量量化的技术,它通过选择部分卷积核进行量化,逐步提高量化比例,实现从半精度到全精度的迁移。本文探讨了SQ方法的关键组件,包括粒度选择、量化概率函数及更新方案,并详细介绍了实验设置。
SQ是一种用于神经网络权重增量量化的技术,它通过选择部分卷积核进行量化,逐步提高量化比例,实现从半精度到全精度的迁移。本文探讨了SQ方法的关键组件,包括粒度选择、量化概率函数及更新方案,并详细介绍了实验设置。
















 382
382

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








