每周一算法：多起点最短路

题目描述

有一天，琪琪想乘坐公交车去拜访她的一位朋友。由于琪琪非常容易晕车，所以她想尽快到达朋友家。

现在给定你一张城市交通路线图，上面包含城市的公交站台以及公交线路的具体分布。

已知城市中共包含 $n$个车站（编号$1\sim n$），以及 $m$ 条公交线路。

每条公交线路都是单向的，从一个车站出发直接到达另一个车站，两个车站之间可能存在多条公交线路。

琪琪的朋友住在$s$号车站附近。琪琪可以在任何车站选择换乘其它公共汽车。

请找出琪琪到达她的朋友家（附近的公交车站）需要花费的最少时间。

输入格式

输入包含多组测试数据。

每组测试数据第一行包含三个整数 $n,m,s$，分别表示车站数量，公交线路数量以及朋友家附近车站的编号。

接下来 $m$ 行，每行包含三个整数 $p,q,t$，表示存在一条线路从车站 $p$ 到达车站 $q$，用时为 $t$。

接下来一行，包含一个整数 $w$，表示琪琪家附近共有 $w$ 个车站，她可以在这 $w$ 个车站中选择一个车站作为始发站。

再一行，包含 $w$ 个整数，表示琪琪家附近的 $w$ 个车站的编号。

输出格式

每个测试数据输出一个整数作为结果，表示所需花费的最少时间。

如果无法达到朋友家的车站，则输出 -1。

每个结果占一行。

样例 #1

样例输入 #1

5 8 5
1 2 2
1 5 3
1 3 4
2 4 7
2 5 6
2 3 5
3 5 1
4 5 1
2
2 3
4 3 4
1 2 3
1 3 4
2 3 2
1
1

样例输出 #1

1
-1

提示

【数据范围】

$n\le 1000,m\le 20000$,
$1\le s\le n$,
$0<w<n$,
$0<t\le 1000$

算法思想一：反向建边

根据题目描述，琪琪家附近共有 $w$ 个车站，可以在任何车站选择换乘其它公共汽车，目标是到达$s$号车站附近的朋友家。也就是说起点可以有多个，终点只有$1$个，求从多个起点出发到达终点的最短路。

基于上述分析，可以反向建边，利用单源最短路算法，例如「Dijkstra」或者「SPFA」，求终点到所有起点的最短路，然后打擂台求一个最小值即可。

时间复杂度

这里使用「SPFA」求最短路，其平均时间复杂度为$O(kn)$，$k$是一个很小的常数，最坏情况下是$O(nm)$；一共有$T$组测试样例，因此总的时间复杂度为$O(T\times kn)$。

代码实现

#include <bits/stdc++.h>
using namespace std;
const int N = 1005, M = 20005, INF = 0x3f3f3f3f; 
int h[N], e[M], w[M], ne[M], idx;
int n, m, s, t, p[N], dis[N], q[N], st[N];
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
void spfa()
{
    memset(dis, 0x3f, sizeof dis);
    int hh = 0, tt = 0;
    dis[s] = 0; st[s] = 1; q[tt ++] = s;
    while(hh != tt) //循环队列
    {
        int u = q[hh ++];
        if(hh == N) hh = 0; //循环队列
        st[u] = 0;
        for(int i = h[u]; ~ i; i = ne[i])
        {
            int v = e[i];
            if(dis[v] > dis[u] + w[i])
            {
                dis[v] = dis[u] + w[i];
                if(!st[v])
                {
                    st[v] = 1; q[tt ++] = v;
                    if(tt == N) tt = 0; //循环队列
                }
            }
        }
    }
}

int main()
{
    while(scanf("%d%d%d", &n, &m, &s) != -1)
    {
        memset(h, -1, sizeof h);
        idx = 0; //多组测试样例，需要重置idx
        for(int i = 0; i < m; i ++)
        {
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            add(b, a, c); //反向建边
        }
        scanf("%d", &t);
        for(int i = 0; i < t; i ++) scanf("%d", &p[i]);
        spfa();
        int ans = INF;
        for(int i = 0; i < t; i ++) ans = min(ans, dis[p[i]]);
        if(ans == INF) puts("-1");
        else printf("%d\n", ans);
    }    
    return 0;
}

算法思想二：虚拟源点

反向建边的思想可以解决从多个起点出发到达终点的最短路问题，但是当终点也有多个时，则无法处理。此时，除了「Floyd」算法之外，还可以使用虚拟源点的思想来处理。

基本思想就是设置一个虚拟源点，从该源点到每个起点建立一条权重为0的边。如下图所示：

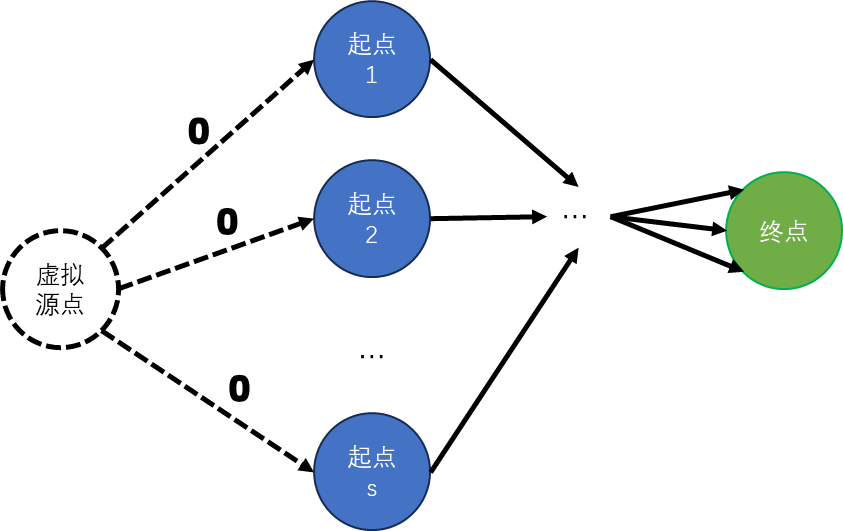
这样，对于每条从起点到终点的最短路，都可以对应一条从虚拟源点出发，经过起点到达终点的最短路。这样就可以利用单源最短路算法，例如「Dijkstra」或者「SPFA」，直接求虚拟源点到终点的最短路即可。

代码实现

#include <bits/stdc++.h>
using namespace std;
//注意，由于引入了虚拟节点，边数要相应增加
const int N = 1005, M = 21005, INF = 0x3f3f3f3f; 
int h[N], e[M], w[M], ne[M], idx;
int n, m, s, t, q[N], dis[N], st[N];
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int spfa()
{
    memset(dis, 0x3f, sizeof dis);
    int hh = 0, tt = 0;
    dis[0] = 0; st[0] = 1; q[tt ++] = 0; //将虚拟源点0加入队列
    while(hh != tt) //循环队列
    {
        int u = q[hh ++];
        if(hh == N) hh = 0; //循环队列
        st[u] = 0;
        for(int i = h[u]; ~ i; i = ne[i])
        {
            int v = e[i];
            if(dis[v] > dis[u] + w[i])
            {
                dis[v] = dis[u] + w[i];
                if(!st[v])
                {
                    st[v] = 1; q[tt ++] = v;
                    if(tt == N) tt = 0; //循环队列
                }
            }
        }
    }
    if(dis[s] == INF) return -1;
    else return dis[s];
}

int main()
{
    while(scanf("%d%d%d", &n, &m, &s) != -1)
    {
        memset(h, -1, sizeof h);
        idx = 0; //多组测试样例，需要重置idx
        for(int i = 0; i < m; i ++)
        {
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            add(a, b, c); //正向建边
        }
        scanf("%d", &t); //输入起点个数
        for(int i = 0; i < t; i ++) 
        {
            int s;
            scanf("%d", &s);
            add(0, s, 0); //从虚拟源点0建一条权重为0、指向起点s的边
        }
        printf("%d\n", spfa());
    }
    
    return 0;
}