2023年CSP-S1提高级第一轮题解

一、单项选择（30分）

（共15题，每题2分，共计30分：每题有且仅有一个正确选项）

1. 在 Linux 系统终端中，以下哪个命令用于创建一个新的目录？

• A. newdir
• B. mkdir
• C. create
• D. mkfolder

答案为mkdir。
Linux中常用的跟目录和文件相关的命令有：

• pwd：显示当前工作目录的绝对路径
• cd：用于切换当前工作目录
• ls：列出目录内容
• echo：终端输出文本字符串或者变量的值，例如：echo "Hello, World!"
• mkdir ：创建新目录
• rmdir：删除空目录
• touch file.txt # 创建名为 file.txt 的空文件
• rm -r non_empty_dir # 递归删除目录（包括子目录和文件）

2. $0,1,2,3,4$中选取$4$个数字，能组成（ ）个不同四位数。（注：最小的四位数是$1000$，最大的四位数是$9999$）

• A. $96$
• B. $18$
• C. $120$
• D. $84$

利用乘法原理：

• 千位不能为$0$，有$4$种选择
• 百位有$4$种选择
• 十位有$3$种选择
• 个位有$2$种选择

答案为：$4\times 4\times 3\times 2=96$

3. 假设 $n$ 是图的顶点的个数，$m$ 是图的边的个数，为求解某一问题有下面四种不同时间复杂度的算法。对于 $m=\theta (n)$ 的稀疏图而言，下面的四个选项，哪一项的渐近时间复杂度最小。

• A. $O(m\sqrt{logn\times loglogn})$
• B. $O(n^2+m)$
• C. $O(\frac{n^2}{logm}+mlogn)$
• D. $O(m+nlogn)$

稀疏图指的是边的数量$m$远小于$n^2$的情况，通常认为$m$大约是$O(n)$或者$O(nlogn)$这样的数量级，而稠密图$m$接近$n^2$。对于$m=\theta (n)$的稀疏图，不妨将$4$个选项中的$m$都替换为$n$，

• B选项$O(n^2+n)$
• C选项$O(\frac{n^2}{logn}+nlogn)$，$\frac{n^2}{logn}<n^2$，$nlogn<n^2$，所以C选项的时间复杂度优于B。
• D选项$O(n+nlogn)$，$n<\frac{n^2}{logn}$，所以D选项的时间复杂度优于C。
• A选项$O(n\sqrt{logn\times loglogn})$，$\sqrt{logn\times loglogn}<logn$，所以A选项的时间复杂度优于D。

时间复杂度从大到小依次为$B>C>D>A$。

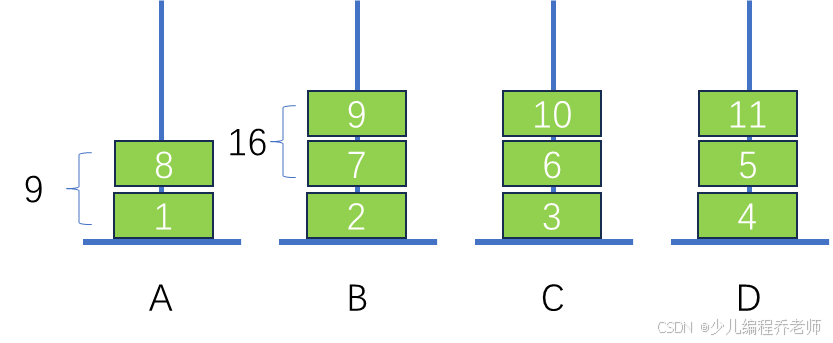
4. 假设有$n$根柱子，需要按照以下规则依次放置编号为$1,2,3,...$ 的圆环：每根柱子的底部固定，顶部可以放入圆环，每次从柱子顶部放入圆环时，需要保证任何两个相邻圆环的编号之和是一个完全平方数。请计算当有 $4$ 根柱子时，最多可以放置（ ）个圆环。

• A. $7$
• B. $9$
• C. $11$
• D. $5$
  

5. 以下对数据结构的表述不恰当的一项是：（ ）。

• A. 队列是一种先进先出（FIFO）的线性结构
• B. 哈夫曼树的构造过程主要是为了实现图的深度优先搜索
• C. 散列表是一种通过散列函数将关键字映射到存储位置的数据结构
• D. 二叉树是一种每个结点最多有两个子结点的树结构

哈夫曼树（Huffman Tree）是利用贪心构建的一种带权路径最短的二叉树，主要用于数据压缩领域，通过为高频符号分配短编码、低频符号分配长编码，实现数据的高效无损压缩。

6. 以下连通无向图中，（ ）一定可以用不超过两种颜色进行染色

• A. 完全三叉树
• B. 平面图
• C. 边双连通图
• D. 欧拉图

可以用不超过两种颜色进行染色的无向连通图可以构成二分图。二分图（Bipartite Graph） 的顶点集可被划分为两个互不相交的独立子集，使得所有边均连接不同子集的顶点。二分图的核心条件就是不含任何奇数长度的环，如三角形、五边形等。

• 完全三叉树由于不包含环，一定可以构成二分图
• 三角形属于平面图，存在奇数长度的环，不能构成二分图
• 边双连通图是指图中不存在桥（Bridge），即任意删除一条边后，图仍保持连通。三角形也属于边双连通图。
• 欧拉图的核心特性是存在一条经过图中每条边恰好一次的闭合路径，即从起点出发，经过每条边恰好一次又回到起点，这样的路径又称为欧拉回路。三角形也是欧拉图。

7. 最长公共子序列长度常常用来衡量两个序列的相似度。其定义如下：给定两个序列$X=x_1,x_2,x_3,...,x_m$ 和$Y=y_1,y_2,y_3,...,y_n$, 最长公共子序列（LCS）问题的目标是找到一个最长的新序列$Z=z_1,z_2,z_3,...,z_k$ 使得序列$Z$既是序列$X$的子序列，又是序列$Y$ 的子序列，且序列 $Z$的长度$k$ 在满足上述条件的序列里是最大的。（注: 序列$A$ 是序列$B$ 的子序列，当且仅当在保持序列$B$ 元素顺序的情况下，从序列$B$ 中删除若干个元素，可以使得剩余的元素构成序列 $A$。）则序列 ABCAAAABA 和 ABABCBABA 的最长公共子序列长度为（ ）

• A. $4$
• B. $5$
• C. $6$
• D. $7$

序列 ABCAAAABA 和 ABABCBABA 的最长公共子序列为ABCABA，长度为$6$。

8. 一位玩家正在玩一个特殊的掷骰子的游戏，游戏要求连续掷两次骰子，收益规则如下: 玩家第一次掷出$x$点，得到$2x$ 元；第二次掷出$y$ 点，当$y=x$ 时玩家会失去之前得到的$2x$ 元;而当 $y\ne x$时玩家能保住第一次获得的$2x$ 元。上述$x,y\in 1,2,3,4,5,6$。例如: 玩家第一次掷出$3$ 点得到 $6$ 元后，但第二次再次掷出$3$ 点，会失去之前得到的$6$ 元，玩家最终收益为$0$ 元;如果玩家第一次掷出 $3$ 点、第二次掷出$4$ 点，则最终收益是$6$ 元。假设骰子挑出任意一点的概率均为$\frac{1}{6}$，玩家连续掷两次骰子后，所有可能情形下收益的平均值是多少?

• A. $7$
• B. $\frac{35}{6}$
• C. $\frac{16}{3}$
• D. $\frac{19}{3}$

每次游戏掷出不同点数得到$2x$元，掷出相同点数得到$0$元，因此计算平均收益（数学期望）时，只需要累加掷出不同点数的概率×收益即可。
每次掷出不同点数的概率都为$\frac{5}{36}$，例如第一次掷出$1$点的概率为$\frac{1}{6}$，第二次掷出不同点数的概率为$\frac{5}{6}$，则第一次掷出$1$点，第二掷出不同点数的概率为$\frac{1}{6}\times \frac{5}{6}=\frac{5}{36}$，此时收益为$2\times 1=2$。
所有可能情形下收益的平均值（数学期望）$=2\times \frac{5}{36}+4\times \frac{5}{36}+6\times \frac{5}{36}+8\times \frac{5}{36}+10\times \frac{5}{36}+12\times \frac{5}{36}=\frac{10+20+30+40+50+60}{36}=\frac{35}{6}$

9. 假设我们有以下的 C++ 代码：

int a = 5, b = 3, c = 4;
bool res = a & b || c ^ b && a | c;

请问，res 的值是什么? （ ）

提示：在 C++ 中，逻辑运算的优先级从高到低依次为：逻辑非（!）、逻辑与（&&）、逻辑或（||）。位运算的优先级从高到低依次为：位非（~）、位与（&）、位异或（^）、位或 （|）。同时，双目位运算的优先级高于双目逻辑运算；逻辑非和位非优先级相同，且高于所有双目运算符。

• A. true
• B. false
• C. 1
• D. 0

5 & 3 = 1
4 ^ 3 = 7
5 | 4 = 5
1 || 7 && 5 = true

10. 假设快速排序算法的输入是一个长度为 $n$ 的已排序数组，且该快速排序算法在分治过程总是选择第一个元素作为基准元素。以下哪个选项描述的是在这种情况下的快速排序行为？

• A. 快速排序对于此类输入的表现最好，因为数组已经排序
• B. 快速排序对于此类输入的时间复杂度是$O(nlogn)$。
• C. 快速排序对于此类输入的时间复杂度是 $O(n^2)$
• D. 快速排序无法对此类数组进行排序，因为数组已经排序

对于已经有序的序列进行快速排序，且在分治过程总是选择第一个元素作为基准元素，会导致每次分区只有一个元素在左边，剩下的元素都在右边，从而递归的层数接近$n$，时间复杂度退化为$O(n^2)$。

11. 以下哪个命令，能将一个名为 main.cpp 的 C++ 源文件，编译并生成一个名为 main 的可执行文件？（ ）

• A. g++ -o main main.cpp
• B. g++ -o main.cpp main
• C. g++ main -o main.cpp
• D. g++ main.cpp -o main.cpp

在 Linux/macOS 环境下，C++ 的编译通常使用 g++ 。以下是常用编译命令和场景说明
g++ [选项] 源文件 -o 输出文件，例如：g++ main.cpp -o myprogram，其中main.cpp表示源代码文件，-o myprogram指定输出文件名（省略则默认生成 a.exe）。
A选项中，源文件写在输出文件后也是正确的。

12. 在图论中，树的重心是树上的一个结点，以该结点为根时，使得其所有的子树中结点数最多的子树的结点数最少。一棵树可能有多个重心。请问下面哪种树一定只有一个重心？

• A. $4$ 个结点的树
• B. $6$ 个结点的树
• C. $7$ 个结点的树
• D. $8$ 个结点的树

树的重心数量取决于树的结构，通常有以下两种情况：

• 单重心：常见于节点数为奇数的树，尤其是链状结构或不对称树。示例：
  
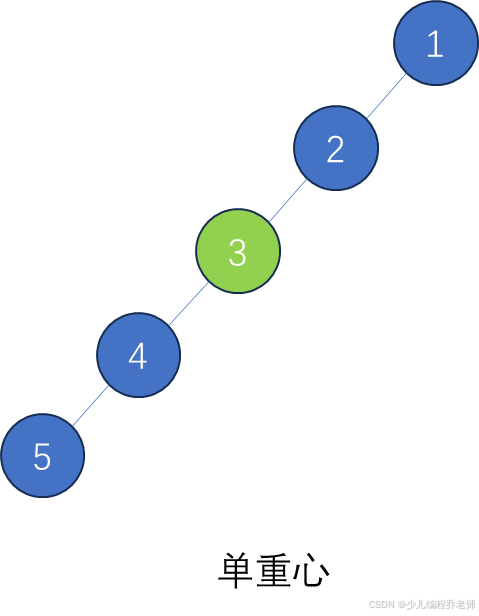
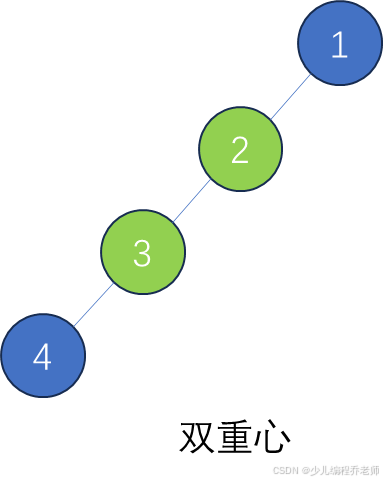
• 双重心：常见于节点数为偶数的链状树或对称结构，两个重心必相邻。
  

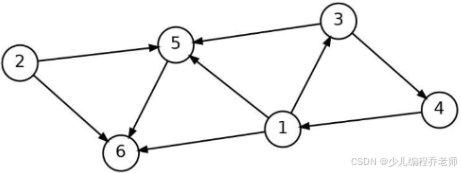
13. 如图是一张包含$6$ 个顶点的有向图，但顶点间不存在拓扑序。如果要删除其中一条边，使这$6$ 个顶点能进行拓扑排序，请问总共有多少条边可以作为候选的被删除边（）。
    

• A. $1$
• B. $2$
• C. 3