luoguP1074 靶形数独

小城和小华都是热爱数学的好学生，最近，他们不约而同地迷上了数独游戏，好胜的他们想用数独来一比高低。但普通的数独对他们来说都过于简单了，于是他们向 Z 博士请教，Z 博士拿出了他最近发明的“靶形数独”，作为这两个孩子比试的题目。

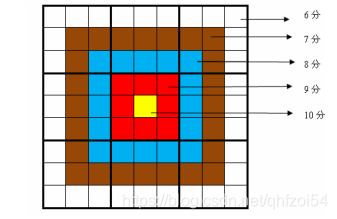
靶形数独的方格同普通数独一样，在 99 格宽×99 格高的大九宫格中有9 9 个 33 格宽×33 格高的小九宫格（用粗黑色线隔开的）。在这个大九宫格中，有一些数字是已知的，根据这些数字，利用逻辑推理，在其他的空格上填入 11 到 9 9的数字。每个数字在每个小九宫格内不能重复出现，每个数字在每行、每列也不能重复出现。但靶形数独有一点和普通数独不同，即每一个方格都有一个分值，而且如同一个靶子一样，离中心越近则分值越高。（如图）

这是一道搜索好题，挺考验剪枝技巧的，但其实普通dfs+剪枝也可以水过
算了，我们来说一下这题的正确做法。首先，很正常的思路是尝试各种剪枝：可行性、最优性…,事实证明效果并不好，只快了一点点。

但是这题的要点是搜索顺序，我们要先考虑可能性较少的点，这听上去很玄学，但是大家仔细想一下，应该可以明白（解释在下面）
如果一个棵搜索树在开始时就很大（对应着开始尝试的点有很多种可能），后面就算再小，分支也很多，但如果开始我们就剪掉一些枝（选择可能性少的），因为第一层剪掉一种情况的节点数量远比第二层、第三层多，这也是一种最优性剪枝的优化方法。

#include<iostream>
#include<algorithm>
using namespace std;
int ans[13][13];
int cntc[13],cntr[13],cntb[13];
int belong(int x,int y){
	int h,l;
	if(x<=3)h=1;
	else if(x<=6)h=2;
	else h=3;
	if(y<=3)l=1;
	else if(y<=6)l=2;
	else l=3;
	return (h-1)*3+l;
}
pair<int,int> s[100];
int cnt=0;
int ANS=0;
int v[10][10]={{0,0,0,0,0,0,0,0,0,0},{0,6,6,6,6,6,6,6,6,6},{0,6,7,7,7,7,7,7,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,9,10,9,8,7,6,},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,7,7,7,7,7,7,6},{0,6,6,6,6,6,6,6,6,6}};
void calc(){
	int tot=0;
	for(int i=1;i<=9;i++)
		for(int j=1;j<=9;j++)
			tot+=ans[i][j]*v[i][j];
	ANS=max(ANS,tot);//统计最大值
}
int col[20][20],row[20][20],block[20][20];
void dfs(int x,int y,int now){
	if(now==cnt+1)calc();
	int b=belong(x,y);
	for(int i=1;i<=9;i++){
		if(!col[x][i]&&!row[y][i]&&!block[b][i]){
			col[x][i]=row[y][i]=block[b][i]=1;
			ans[x][y]=i;
			dfs(s[now+1].first,s[now+1].second,now+1);
			col[x][i]=row[y][i]=block[b][i]=ans[x][y]=0;//标记撤销
		}
	}
}
int vis[20][20];
int main(){
	for(int i=1;i<=9;i++)
		for(int j=1;j<=9;j++){
			cin>>ans[i][j];
			if(ans[i][j]!=0)vis[i][j]=1,cntc[i]++,cntr[j]++,cntb[belong(i,j)]++,col[i][ans[i][j]]=1,row[j][ans[i][j]]=1,block[belong(i,j)][ans[i][j]]=1;		
			else cnt++;
		}
	//这里就是枚举每一个点的约束数量，约束越多，可能性越小
	//枚举到一个以后，就把能被这个点约束的点约数个数重新统计
	//记录约数个数的顺序，也就是枚举顺序，并且按照这个顺序dfs
	for(int k=1;k<=cnt;k++){
		int Max=0,px,py;
		for(int i=1;i<=9;i++)
			for(int j=1;j<=9;j++)
				if(cntc[i]+cntr[j]+cntb[belong(i,j)]>Max&&!vis[i][j])
				Max=cntc[i]+cntr[j]+cntb[belong(i,j)],px=i,py=j;
		s[k]=make_pair(px,py);
		cntc[px]++,cntr[py]++,cntb[belong(px,py)]++;
		vis[px][py]=1;
	//	cout<<k<<" "<<px<<" "<<py<<endl;	
	}
	dfs(s[1].first,s[1].second,1);
	if(ANS!=0)
	cout<<ANS<<endl;
	else cout<<-1<<endl;
}