洛谷P7917 【洛谷月赛LGR-096 Div.2 T1】 [Kubic] Addition题解

这道题真是让我深刻地陷入了对我智商的怀疑。。。比赛想了50min，结果最后评出来难度是

过分了啊。。。

题目大意

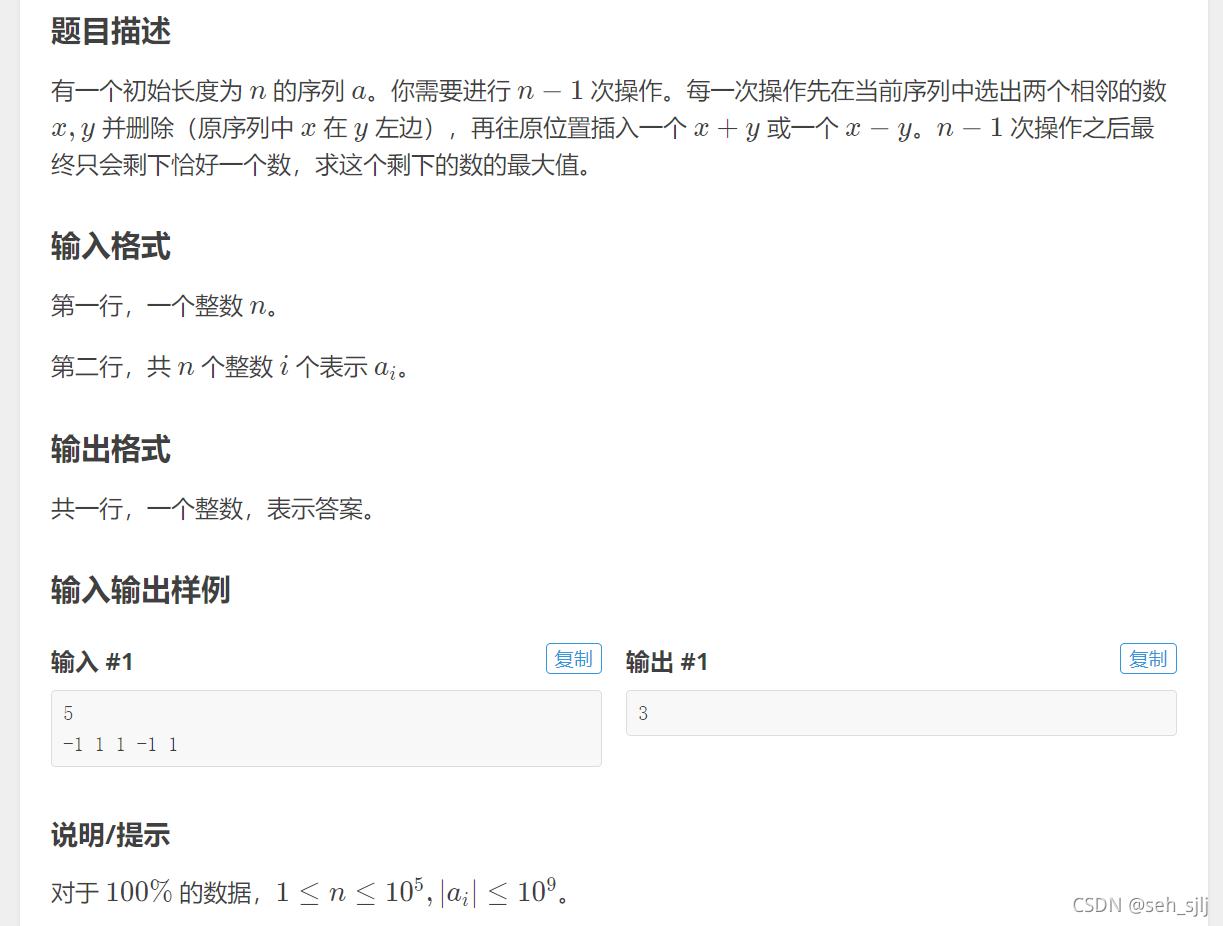
解题思路

贪心。
可以看出，每个数$a_i$对答案的贡献是$\pm a_i$。（因为它要么被减，要么被加。）那么我们尽量让每个数的贡献为其绝对值。又注意到$a_1$的贡献永远是$a_1$本身（因为没有哪个数能减它）。那么，最优解就是$a_1+\sum _{i=2}^n|a_i|$。
下面证明最优解一定可以构造出来。考虑从右往左合并，对于当前数$a_i$和合并其右边的数已经得到的数$\pm \sum _{j=i+1}^n|a_j|$，若$a_i$和$\pm \sum _{j=i+1}^n|a_j|$同号，则执行$x+y$，否则执行$x-y$，使得后$i$个数得到的和为$\pm \sum _{j=i}^n|a_j|$。最终答案就是$a_1+\sum _{i=2}^n|a_i|$。
时间复杂度：$O(n)$。

奉上高清无码Code：

#include <cstdio>
#include <cstdlib>
#include <cctype>

using namespace std;

typedef long long ll;

ll n;

inline ll read() // 快速读入
{
    ll ret = 0;
    char sgn = 0;
    char c;
    while(!isdigit(c = getchar())) if(c == '-') sgn = 1;
    ret = c ^ 48;
    while(isdigit(c = getchar())) ret = (ret << 1) + (ret << 3) + (c ^ 48);
    return sgn ? -ret : ret;
}

int main()
{
    n = read();
    ll ans = read(); // ans = a[1]
    while(--n) ans += llabs(read());
    // ans += |a[2]| + |a[3]| + ... + |a[n]|
    printf("%lld\n", ans);
    return 0;
}

---

如果还不理解的话，举个栗子：

5
-1 2 -3 4 -5

$4-(-5)\to (-1,2,-3,9)$
$-3-9\to (-1,2,-12)$
$2-(-12)\to -1,14$
$-1+14\to 13$
答案就是$13=-1+|2|+|-3|+|4|+|-5|=a_1+\sum _{i=2}^n|a_i|$。