PTA 1033 To Fill or Not to Fill

最新推荐文章于 2022-10-20 07:58:34 发布

huang balloon

最新推荐文章于 2022-10-20 07:58:34 发布

阅读量91

点赞数

CC 4.0 BY-SA版权

分类专栏： PAT 文章标签：贪心算法算法

本文链接：https://blog.youkuaiyun.com/qaqaqa666/article/details/113771366

PAT 专栏收录该内容

87 篇文章

订阅专栏

本文介绍了一种基于贪心策略的算法，用于确定最优的加油路径，确保车辆在多个加油站间行驶的成本最低。算法首先对加油站按距离排序，并采用最优选择策略来决定在哪个加油站补充燃油。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

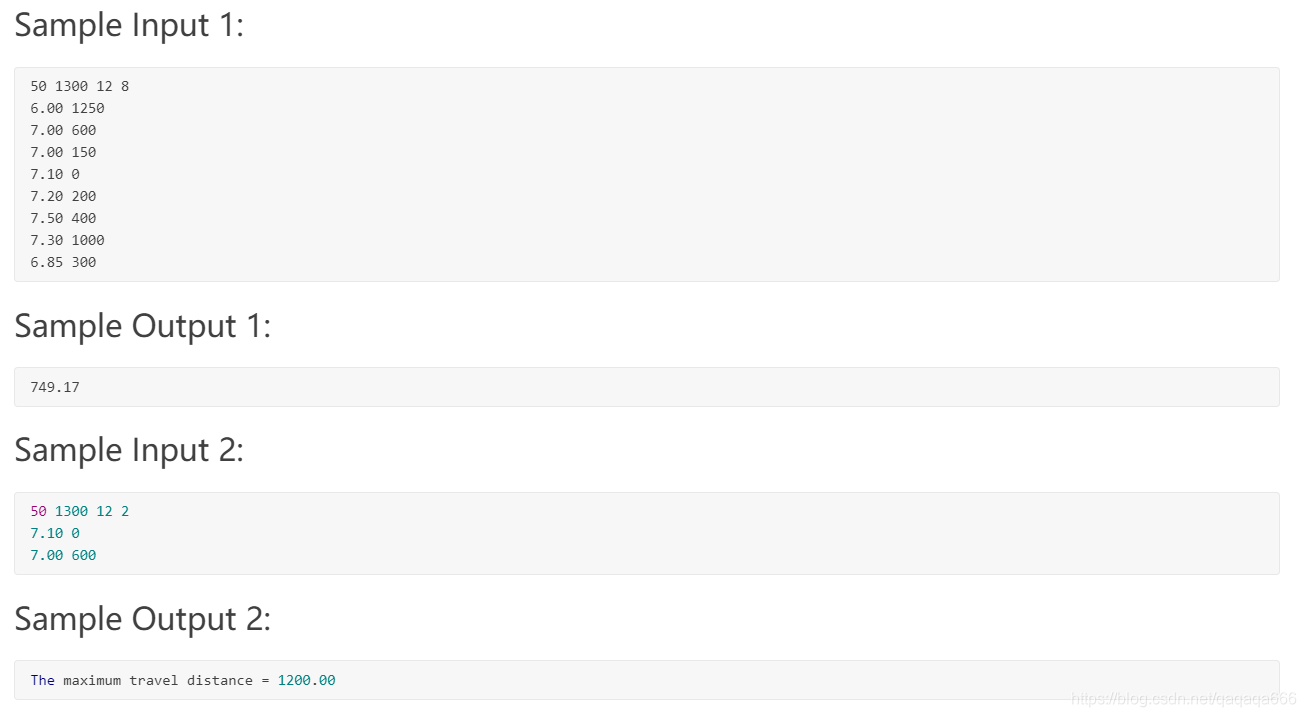
在这里插入图片描述

分析：

运用贪心策略，每一步尽可能用最便宜的油价。

先按距离进行排序，假如起始位置也就是距离最近的加油站的距离不是0，那么直接输出最远行驶距离为0；
从当前加油站出发，在满油状态下能到达的所有加油站中寻找距离当前加油站最近且油价低于当前油价的加油站（优先前往油价更低油价的加油站）
如果找不到油价低于当前油价的加油站，则寻找油价最低的加油站
满油下找不到能到达的加油站，则说明不能到达目的地

#include<iostream>
#include<algorithm>
using namespace std;
struct station{
	double price,dis;
}st[505];
bool cmp(station a,station b){
	return a.dis<b.dis;
}
int main(){
	int n;
	double Cmax,D,Davg;
	cin>>Cmax>>D>>Davg>>n;
	for(int i=0;i<n;i++){
		cin>>st[i].price>>st[i].dis;
	}
	st[n].price=0;
	st[n].dis=D;
	sort(st,st+n,cmp);
	if(st[0].dis!=0){
		cout<<"The maximum travel distance = 0.00"<<endl;
	}
	else{
		int now=0;
		double ans=0;
		double nowTank=0;
		double maxdis=Cmax*Davg;
		while(now<n){
			int k=-1;
			double priceMin=1e9;
			for(int i=now+1;i<=n&&st[i].dis-st[now].dis<=maxdis;i++){
				if(st[i].price<priceMin){
					priceMin=st[i].price;
					k=i;
					if(priceMin<st[now].price){
						break;
					}
				}
			}
			if(k==-1) break;
			double need=(st[k].dis-st[now].dis)/Davg;
			if(priceMin<st[now].price){
				if(nowTank<need){
					ans+=(need-nowTank)*st[now].price;
					nowTank=0;
				}
				else{
					nowTank-=need;
				}
			}
			else{
				ans+=(Cmax-nowTank)*st[now].price;
				nowTank=Cmax-need;
			}
			now =k;
		}
		if(now==n){
			printf("%.2f\n",ans);
		}
		else{
			printf("The maximum travel distance = %.2f\n",st[now].dis+maxdis);
		}
	}
	return 0;
}