高阶OTA-C滤波器可测性设计

高阶OTA‐C滤波器的可测性设计

马苏德‐乌尔·哈桑1,朱艳青2,1,* †和孙一昌1
1赫特福德郡大学工程与技术学院，英国哈特菲尔德
2湖南大学电气与信息工程学院， 中国长沙

摘要

本文提出了一种针对高阶跨导运算放大器‐C（OTA‐C）滤波器的基于振荡测试方法的研究。该方法基于将高阶滤波器划分为二阶滤波器功能模块。通过开启Q环和增加正反馈技术，将二阶滤波器部分转换为正交振荡器。这些技术基于开环结构以及附加的正反馈结构。文中给出了两种可测性设计方法在n阶级联、IFLF和跃蛙（LF）滤波器中的实现，并讨论了改进电路的面积开销。同时对所提技术的性能进行了研究。设计并仿真了四阶级联、逆前导反馈（IFLF）和LFOTA‐C滤波器，利用基于模拟多路复用器的增加正反馈方法进行故障覆盖率分析。仿真结果表明，采用正反馈的基于振荡测试方法对级联、IFLF和LFOTA‐C滤波器分别提供了约97%、96%和95%的高故障覆盖率。版权所有©2016约翰威立父子有限公司

2016年6月11日收到；2016年1月7日修订；2016年1月20日接受

关键词 ：电路测试；基于振荡的测试；OTA‐C滤波器；高阶滤波器

1. 引言

基于振荡的测试（OBT）是一种用于模拟电路的低成本方法。该方法的基本思想是将被测电路转换为一个振荡器[1–3]，通过添加反馈电路，在测试模式下产生自持振荡。振荡频率（f OSC）通常用作故障特征。OBT方法非常有前景，因为它不需要外部测试激励，且附加的测试电路可以方便地嵌入到被测电路中。OBT技术已应用于多种模拟和混合信号电路[4–10]。由于有源模拟滤波器广泛应用于射频、模拟和混合信号集成电路中，因此针对模拟滤波器的低成本测试已开展了大量OBT研究[11–13]。近期的研究集中在OBT在不同Gm‐C滤波器中的应用[14–19]。这些工作中进行了详尽的仿真与实验，显示出良好的故障覆盖率，与先前方法报道的结果一致。

本文提出的用于高阶OTA‐C滤波器的内建自测方法基于将高阶滤波器划分为二阶滤波器功能，并且与旁路和多路复用方法相比，只需要少量金属氧化物半导体（MOS）开关进行修改。因此，OBT方法对滤波器的性能影响可忽略不计，具有低面积开销、较少的修改量、低功耗和测试时间短的优点。OBT方法使用无向量输出频率比较在无故障和有故障电路之间，从而消除了对输入测试信号和特殊测试设备的需求。

用于高阶OTA‐C滤波器的常用设计方法基于级联和多环反馈结构。反馈网络的选择可形成级联、逆跟随‐领导者反馈（IFLF）和跃蛙（LF）结构[20]。这类多级（高阶）OTA‐C滤波器结构可被修改以实现基于振荡的可测性设计技术。本文提出并讨论了内建自测方法在n阶级联、IFLF和LFOTA‐C滤波器中的应用。同时，设计并仿真了四阶级联、IFLF和LFOTA‐C滤波器，以验证所提方法的有效性。

本文的组织结构如下。第2节讨论了高阶OTA‐C滤波器的OBT结构。第3节讨论了仅使用简单MOS开关将级联、IFLF和LF高阶OTA‐C滤波器的双二次级进行划分并转换为振荡器的方法。第4节提出了利用额外OTA和MOS开关的正反馈方法，用于将高阶滤波器转换为振荡器。第5节介绍了四阶级联、IFLF和LFOTA‐C滤波器的仿真结果。最后，第6节给出了结论。

2. 用于高阶跨导运算放大器‐C滤波器的基于振荡的测试结构

用于高阶OTA‐C滤波器的基于振荡的测试结构是基于将高阶滤波器分解为功能构建模块。滤波器的划分应使得每个独立模块代表一个双二次传递函数。然后，可以通过在其传递函数中建立振荡条件，将这些模块转换为振荡器。振荡条件由巴克豪森准则[2]得出。该准则指出，在振荡频率 ω0下，信号必须在环路中无衰减且无相移地传播。对于正反馈，相移必须为零；而对于负反馈，相移必须为180度，以抵消反馈符号并产生总的相移为零。正交振荡器模型理想上可以用二阶特征方程来描述：

$$
s^2 + bs + \omega_0^2 = 0 \quad (1)
$$

其中V0(s) 是振荡器的输出。当在振荡频率 ω0 时，将发生振荡，n 参数 b = 0。

在测试模式操作期间，每个模块将在一个频率下振荡，该频率是其元件值和跨导放大器跨导的函数。振荡频率相对于模块谐振频率的偏差表明该模块中元件存在故障行为。振荡频率对元件参数变化的灵敏度将决定故障的可检测范围。

实现基于振荡的DFT方法需要对原始滤波器进行以下修改：将滤波器分解为双二次级，相互隔离各个双二次级，并重构每个双二次级的反馈网络，以在其传递函数中建立振荡条件。

所有这些修改均可通过在原始滤波器电路中插入MOS晶体管开关来实现。因此，MOS晶体管是OBT测试中的关键组件，并提供了高阶OTA‐C滤波器的可测结构。晶体管的精度直接影响被测滤波器的精度和功能。晶体管最重要的特性包括导通电阻、关断电阻以及寄生电容器的值。修改后滤波器的性能直接取决于插入开关参数的规格以及开关在电路中的位置。因此，选择最佳尺寸以及在信号路径中合理的位置进行开关插入，将确保被测滤波器的精度和原始功能。

OBT的测试和故障检测过程如下。首先在正常模式下对被测滤波器进行测试，并测量其截止频率。如果截止频率超出给定的容差带，则将激活测试模式。在测试模式下，高阶滤波器被分解为独立的双二次振荡器模块，并测量各个振荡器频率以隔离故障模块。通过比较无故障频率与被测滤波器对应振荡器模块的测量频率，可确定故障级。与无故障频率的偏差将识别出故障类型（灾难性或参数性）以及该级中故障的可能位置。

常用的多级跨导运算放大器‐电容滤波器结构，如级联、IFLF和LF，已被修改以实现所提出的基于振荡的可测性设计技术。在以下章节中，将介绍仅使用MOS开关实现开环Q回路 OBT方法，以及结合MOS开关和额外OTA添加正反馈OBT方法到n阶级联、IFLF和LFOTA‐C滤波器的方法。

3. 仅使用MOS开关测试高阶运算跨导电容滤波器

仅使用MOS开关的开环Q回路OBT方法可应用于任何类型的高阶OTA‐C滤波器，且对原始滤波器性能的影响可忽略不计。面积开销取决于滤波器的类型和阶数。在本节中，我们将介绍将高阶OTA‐C滤波器分解为二阶功能模块的技术，并仅使用MOS开关将其转换为正交振荡器的方法。提出了n阶OTA‐C滤波器的级联、IFLF和LF结构的转换方法，并进行了讨论。

3.1. n阶级联跨导运算放大器‐C滤波器

二阶部分的级联连接是实现高阶滤波器功能最流行且有效的方法。对级联系统的测试需要滤波器内部节点的可控性和可观测性。通过将系统划分为可访问的模块，可以提高可控性和可观测性。级联滤波器结构可以划分为代表双二次传递函数的二阶部分模块。图1展示了仅使用MOS开关的基于OBT的可测性设计架构，其中Sn和Sp分别为NMOS和PMOS晶体管开关。

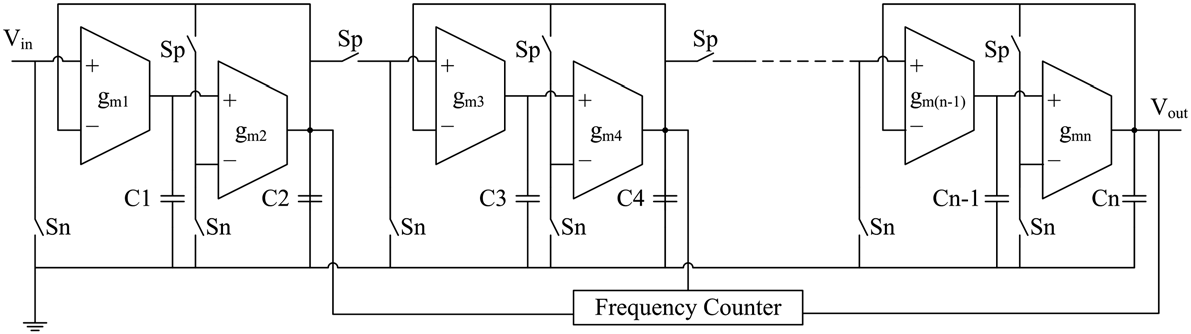
图1中的改进的滤波器电路具有两种操作模式：正常模式和测试模式。在正常模式下，所有标记为Spare的开关均闭合，而标记为Snare的开关则断开，此时电路将执行原始滤波器的功能。每个二阶滤波器的传递函数可推导如下：

$$
H(s) = \frac{V_{out}}{V_{in}} = \frac{g_{mi} g_{i+1}}{C_i C_{i+1} s^2 + \frac{g_{i+1}}{C_{i+1}} s + \frac{g_{mi} g_{i+1}}{C_i C_{i+1}}} \quad i = \text{odd}; i = 1, 3, 5:::n - 1 \quad (2)
$$

其中n为滤波器阶数且为偶数。当n为奇数时，最后一个积分器可与第(n‐1)个积分器结合形成一个振荡器。每个滤波器的截止频率由以下公式给出：

$$
\omega_{0i} = \sqrt{\frac{g_{mi} g_{i+1}}{C_i C_{i+1}}} \quad (3)
$$

当启动测试模式时，Sp开关断开，Sn开关闭合。Sp开关将滤波器分割为双二次级，而 Sn开关通过开启Q环将这些双二次级转换为振荡器。所得振荡器的特征方程可以描述为：

$$
s^2 + \frac{g_{mi} g_{i+1}}{C_i C_{i+1}} = 0 \quad (4)
$$

极点由以下给出：

$$
s_{1,2} = \pm j \sqrt{\frac{g_{mi} g_{i+1}}{C_i C_{i+1}}} \quad (5)
$$

式(3‐5)表明，通过打开Q环可满足振荡条件，且振荡频率即为滤波器的截止频率。

面积开销取决于滤波器的类型和阶数。对于n阶级联滤波器实现仅开关的内建自测方法，需要n个N型金属氧化物半导体（NMOS）晶体管和(n‐1)个P型金属氧化物半导体（PMOS）晶体管。级联结构的相对面积开销可以计算为：

$$
AO_{\text{Cascade}} = \frac{nA_n + (n - 1)A_p}{A} \quad (6)
$$

其中A是原始电路面积，An是开关Sn的面积，Ap是开关Sp的面积。

3.2. n阶IFLF OTA‐C滤波器

IFLF结构由于其简单性、低灵敏度和最少元件数量，是最流行的有源模拟滤波器结构之一，而IFLFOTA‐C滤波器可通过多环反馈方法得到。在测试时，一个n阶IFLFOTA‐C滤波器需要被划分为二阶部分，但由于存在耦合，该过程可能不像级联结构那样直接。图2展示了仅使用MOS开关的n阶IFLFOTA‐C滤波器的基于OBT的可测性设计架构。

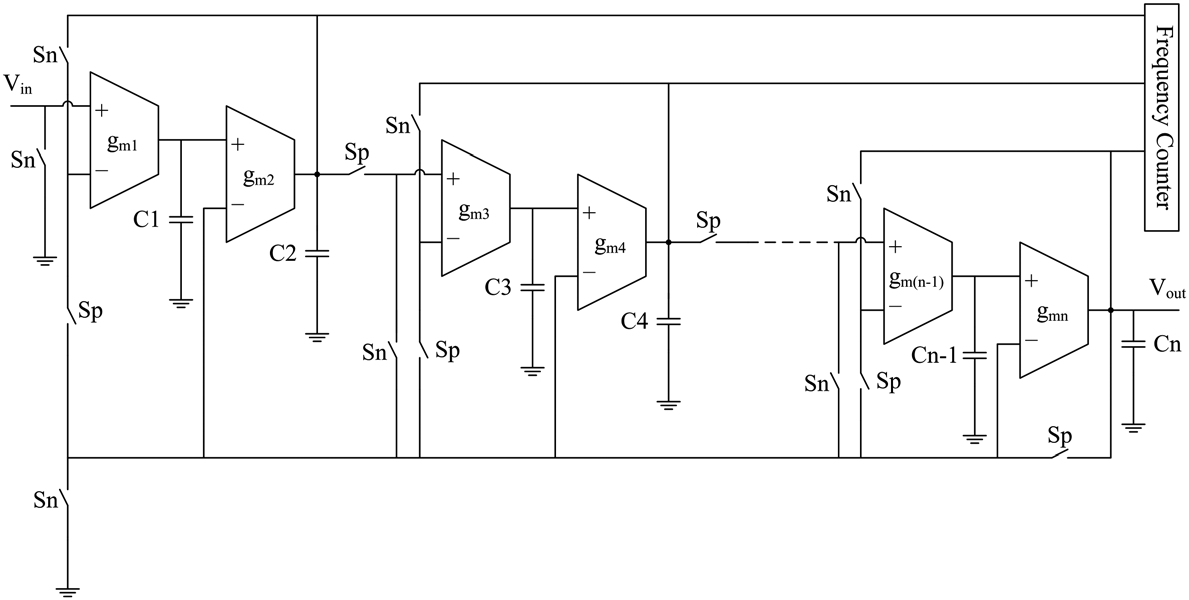
改进型IFLFOTA‐C滤波器也有两种工作模式：正常模式和测试模式。在正常工作模式下，所有Sp开关闭合，Sn开关断开，此时改进后的电路作为从主输入到滤波器输出的高阶滤波器运行。在测试工作模式下，Sp打开开关以充当分路器，并将高阶滤波器分解为各个二阶传递函数模块。通过闭合Sn开关，每个模块被转换为一个振荡器，其振荡频率由公式(3)给出。

IFLF型结构的面积开销大于级联型，因为IFLFOTA‐C滤波器需要在两个反馈环路中进行更改。改进型IFLFOTA‐C滤波器的相对面积开销为：

$$
AO_{\text{IFLF}} = \frac{(n + 1)A_n + nA_p}{A} \quad (7)
$$

其中n为滤波器阶数，A为原始电路面积，An为开关Sn的面积，Ap为开关Sp的面积。

3.3. n阶跃蛙式跨导‐C滤波器

跃蛙结构是多积分器环路反馈OTA‐C滤波器设计中另一种最受欢迎的选择。LF结构具有最小通带幅度灵敏度、最大输入电压和良好的幅频响应的优点。n阶LF滤波器的测试可以仅基于 MOS开关使用OBT方法进行。通过在反馈环路中插入开关，任何偶数阶LF滤波器都可以被划分为二阶传递函数的组合；对于奇数阶滤波器，可将最后一个积分器与倒数第二个积分器结合形成一个二阶传递函数，其中倒数第二个积分器已在前一个二阶模块中进行了测试。可测试的n阶LFOTA‐C滤波器如图3所示。

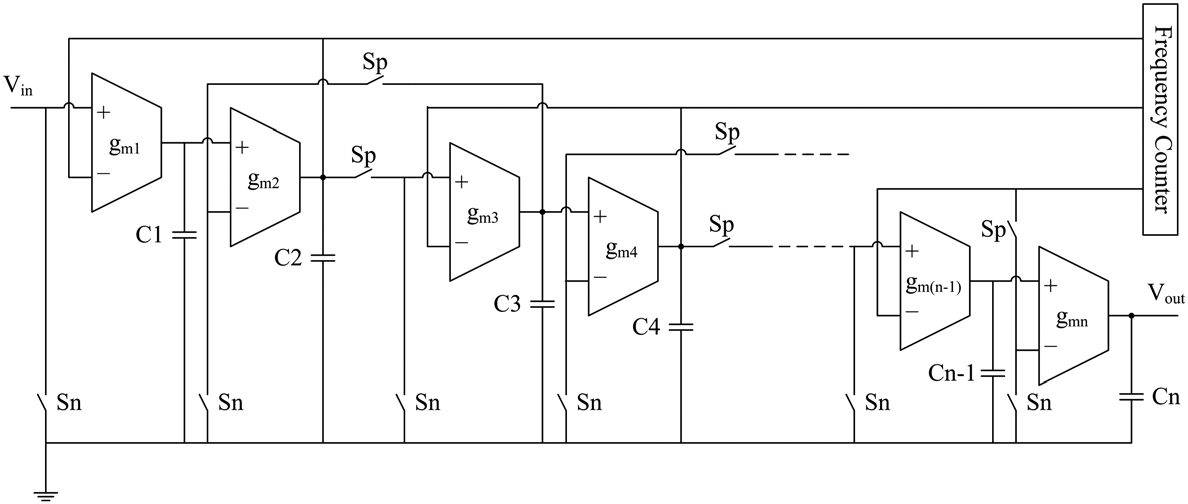
当所有Sp开关闭合且Sn开关断开时，图3中的电路表现为一个性能下降可忽略的n阶低通跨导‐C滤波器。对滤波器性能和精度的影响主要来自Sp开关的寄生电容和导通电阻。这些开关位于信号路径中，必须以最小的导通电阻实现。当通过分别打开和关闭Sp和Sn开关激活测试模式时，该滤波器将转换为正交振荡级。滤波器级的振荡频率取决于该级的跨导和电容值，并由公式(3)给出。改进型n阶LF滤波器结构的相对面积开销由下式给出：

$$
AO_{\text{LF}} = \frac{nA_n + (n - 1)A_p}{A} \quad (8)
$$

LF型结构的面积开销与级联型相同，因为在这两种情况下仅需改变一个反馈回路。

4. 使用附加跨导和MOS开关测试高阶跨导‐C滤波器

正反馈振荡测试法可应用于任意配置类型的高阶OTA‐C滤波器。对于n阶OTA‐C滤波器，正反馈环可通过使用额外OTA、模拟多路复用器和MOS晶体管开关来实现。模拟多路复用器的阶数和MOS开关的数量取决于OTA‐C滤波器的类型和阶数。正反馈环和MOS开关将双二次级转换为具有自启动振荡潜力的二阶振荡系统。以下各小节介绍了正反馈方法在级联、IFLF和LF高阶OTA‐C滤波器中的实现技术。

4.1. 级联高阶跨导运算放大器‐C滤波器

高阶级联OTA‐C滤波器可通过使用最少数量的MOS晶体管开关分解为二阶滤波器部分。将滤波器划分为双二次级所需的开关数量取决于滤波器阶数，对于偶数阶滤波器需要n/2个开关，而对于奇数阶滤波器则需要n/2+ 1个开关。

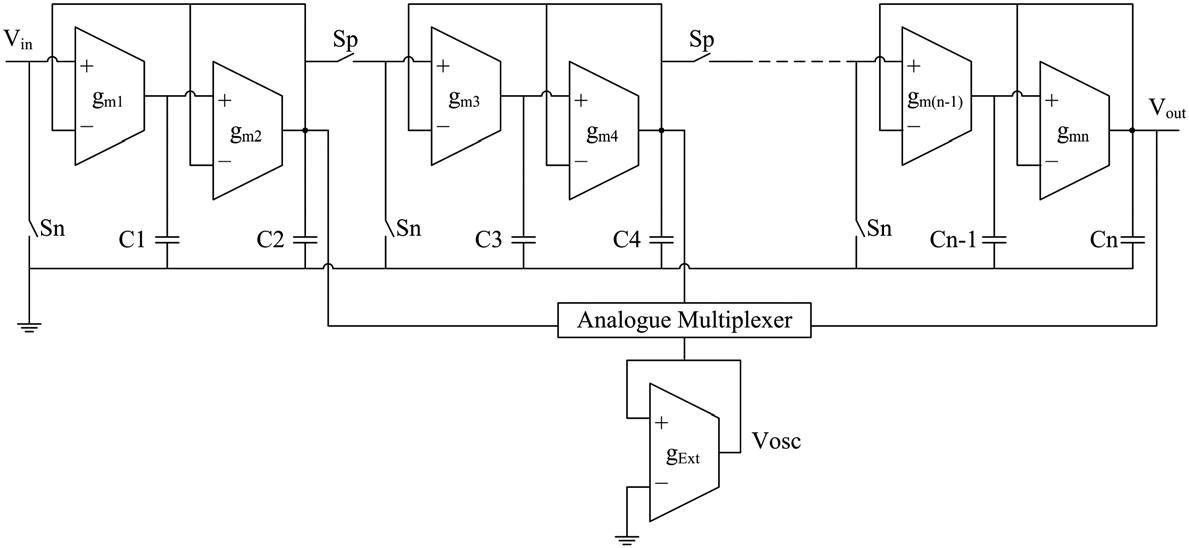
基于正反馈OBT方法的改进型n阶级联跨导‐C滤波器如图4所示。该改进型级联OTA‐C滤波器同样具有两种工作模式：正常模式和测试模式。在正常工作模式下，所有Sp开关闭合，Sn开关断开；此时改进电路作为高阶滤波器工作。在测试模式下，Sp开关断开，将高阶滤波器分解为多个独立的二阶传递函数模块。当Sn开关闭合时，每个双二次级将转换为一个振荡器，同时额外OTA通过模拟多路复用器连接到相应的输出节点。该振荡器的二阶特征方程为：

$$
V_o(s) \left( s^2 + \frac{g_{i+1} - g_{\text{Ext}}}{C_{i+1}} s + \frac{g_{mi} g_{i+1}}{C_i C_{i+1}} \right) = 0 \quad (9)
$$

其中V0(s)是振荡器的输出，且振荡频率 ωo和振荡参数 b 是给定的 by:

$$
\omega_0 = \sqrt{\frac{g_{mi} g_{i+1}}{C_i C_{i+1}}} \quad (10)
$$

$$
b = \frac{g_{i+1} - g_{\text{Ext}}}{C_{i+1}} \quad (11)
$$

公式(10)和(11)表明，出现在b的表达式中的跨导与 ωo的跨导不同。我们可以通过调节跨导gExt来设置振荡条件，而不会影响振荡器频率。因此，使用额外OTA可以实现对振荡条件的更好的可控性。在n阶级联滤波器中实现正反馈OBT方法需要n/2个NMOS和n/2个PMOS晶体管。相对面积开销可计算为：

$$
AO_{\text{Cascade}} = \frac{nA_n + (n - 1)A_p + 2A_{am} + 2A_{\text{Ext}}}{2A} \quad (12)
$$

其中n为滤波器阶数，A为原始电路面积，Aam为模拟多路复用器的面积，AExt为额外OTA的面积，An为开关Sn的面积，Ap为开关Sp的面积。图4中的可测级联滤波器电路具有修改所需元件最少、对滤波器性能影响可忽略、低面积开销、低功耗和测试成本的优点。然而，由于在多路复用域中各级的可测性，修改后的滤波器具有可变测试时间，且测试时间取决于滤波器阶数。若为每个双二次级使用独立OTA和频率计数器，则可实现固定测试时间，但这将带来面积开销、功耗和测试成本方面的代价。

4.2. 反向跟随者反馈高阶跨导运算放大器‐C滤波器

n阶IFLF滤波器可以利用MOS晶体管开关和附加OTA将其划分为双二次级。但由于存在反馈回路，与级联结构相比，它需要几乎两倍数量的MOS开关。IFLF滤波器结构需要两种类型的开关：信号路径中的开关用于将滤波器划分为双二次级，反馈路径中的开关用于断开求和节点并建立振荡条件。基于正反馈OBT方法的可测n阶IFLFOTA‐C滤波器如图5所示。

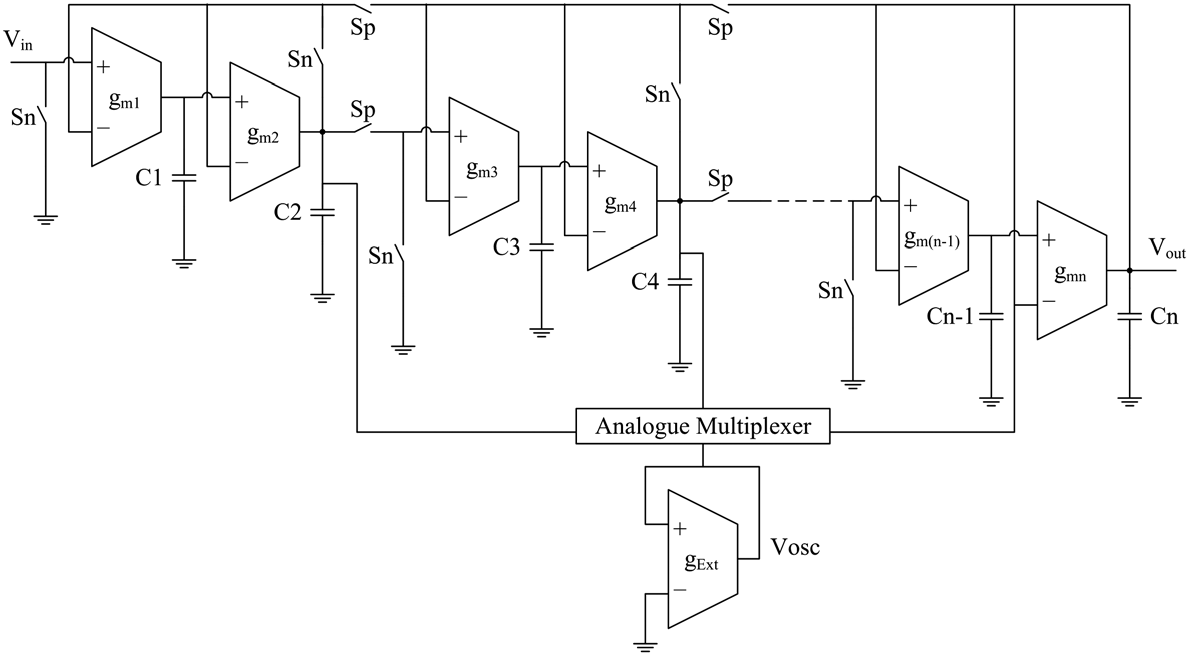
图5中的电路需要一个额外OTA、一个模拟多路复用器和MOS开关，用于划分高阶滤波器并在测试模式下建立振荡条件。振荡频率 ωo和振荡参数b分别由公式(10)和(11)给出。相对面积开销可计算为：

$$
AO_{\text{IFLF}} = \frac{(n - 1)A_n + (n - 2)A_p + A_{am} + A_{\text{Ext}}}{A} \quad (13)
$$

4.3. 跃蛙式高阶运算跨导电容滤波器

将n阶LFOTA‐C滤波器划分为双二次级所需的MOS开关数量与n阶IFLF滤波器相同。这些开关用于断开从偶数个跨导放大器到奇数个跨导放大器的信号路径，以及从奇数个跨导放大器到偶数个跨导放大器的反馈回路。然后，可通过模拟多路复用器利用额外OTA将滤波器的双二次级转换为振荡器。基于正反馈回路OBT方法的改进型n阶LFOTA‐C滤波器如图6所示。

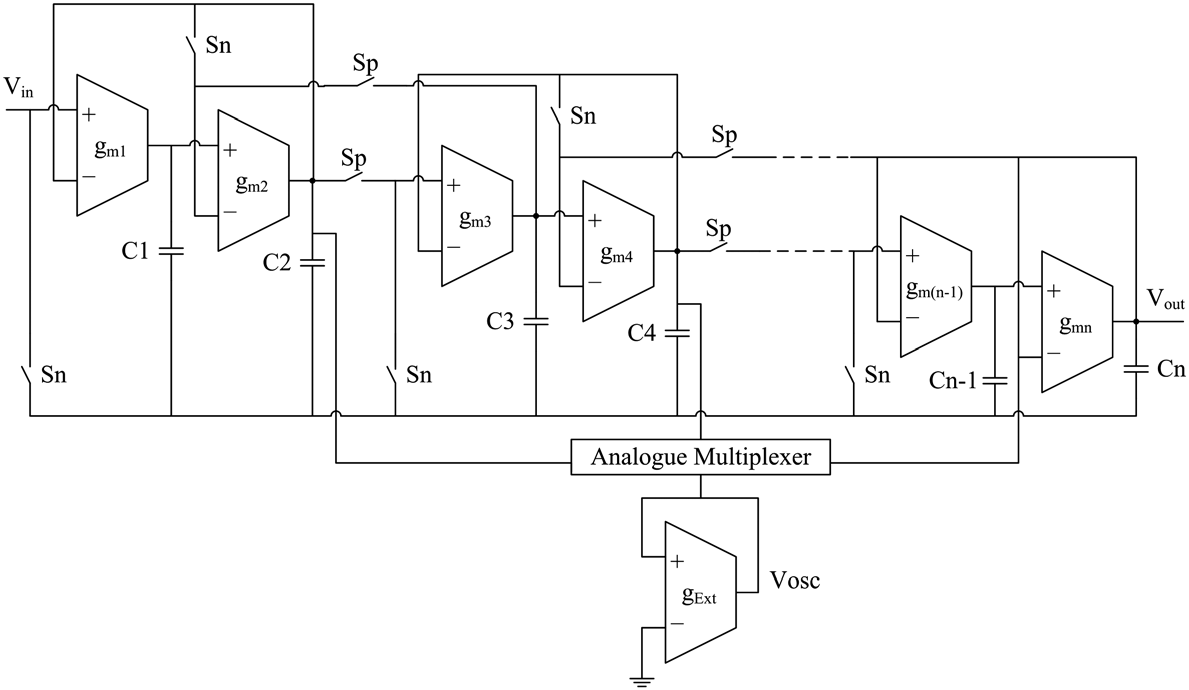
振荡频率 ωo 和振荡参数 b 分别由公式 (10) 和 (11) 给出。相对面积开销可表示为：

$$
AO_{\text{LF}} = \frac{(n - 1)A_n + (n - 2)A_p + A_{am} + A_{\text{Ext}}}{A} \quad (14)
$$

5. 四阶运算跨导电容滤波器的设计与仿真

在第3和第4节中，介绍了用于高阶OTA‐C滤波器的开路Q环法和增加正反馈OBT方法。开路Q环法非常简单，且成本低、芯片面积开销小，因为它仅使用开关。然而，该方法需要两种类型的MOS开关：信号路径中的开关用于将滤波器划分为双二次级，反馈路径中的开关用于建立振荡条件。滤波器结构中额外添加的开关会对高阶滤波器的性能产生显著影响。这些MOS开关的寄生电容和导通电阻会降低滤波器的性能。此外，未包含在振荡器电路中的故障无法被检测到，导致故障覆盖率较低。所有这些问题可以通过在原始滤波器结构中增加一个额外的正反馈环来轻松克服。该正反馈环通过在积分器输出节点处使用一个额外的跨导放大器和MOS开关实现，因此对滤波器的性能影响较小，并通过将滤波器中的所有运算跨导放大器包含在测试中，实现高故障覆盖率。

在我们之前的工作中[15, 16]，案例研究针对双积分环滤波器进行了设计。结果表明，带有MOS开关的双积分环滤波器的截止频率略低于原始滤波器的截止频率。这是因为反馈路径中的MOS开关具有有限的导通电阻和寄生电容。然而，通过增加额外正反馈环路修改后的滤波器性能与原始滤波器非常相似，因为正反馈环仅在测试模式激活时才连接到电路。为了量化所提出的内建自测方法的故障覆盖率和效率，在[15, 16]中的原始滤波器电路中插入了多种不同的灾难性故障和参数性故障。故障检测结果表明，开路Q环法能够检测出所有的灾难性故障以及大部分参数性故障。从开路Q环法的振荡器方程可以看出，那些不影响振荡频率的故障无法被检测到。结果还显示，在增加正反馈方法中，所有注入的故障都通过影响振荡频率表现出来，因此可以被检测到。这些结果表明，用于双积分环滤波器的增加正反馈方法具有高故障覆盖率以及对原始滤波器性能退化较小的优势。

在仅开关的内建自测方法中，问题源于对振荡条件的可控性低。振荡器特征方程(4)表明，振荡频率和振荡条件并非相互独立。因此，参数或寄生偏差会同时改变振荡频率和振荡条件，导致振荡幅度不稳定。相反，使用额外OTA和MOS开关的OBT方法显示，出现在振荡频率表达式中的跨导与出现在振荡条件相应表达式中的跨导不同。这意味着引起振荡频率变化的故障可能不会影响振荡条件。通过调节额外OTA的跨导，可以根据故障或偏差量来调整振荡器的振荡条件。

为了验证所提出的增加正反馈的OBT方法，本文采用[21]中给出的设计方程，设计了四阶低通级联、IFLF和LFOTA‐C滤波器作为案例研究，选定截止频率为50兆赫。采用图7所示的差分输入CMOS跨导放大器来实现OTA‐C滤波器。使用等跨导设计方法设计这些四阶滤波器，标称跨导值为gm = 850μs。在50兆赫进行频率去归一化，得到滤波器的归一化电路电容，如表I所示。

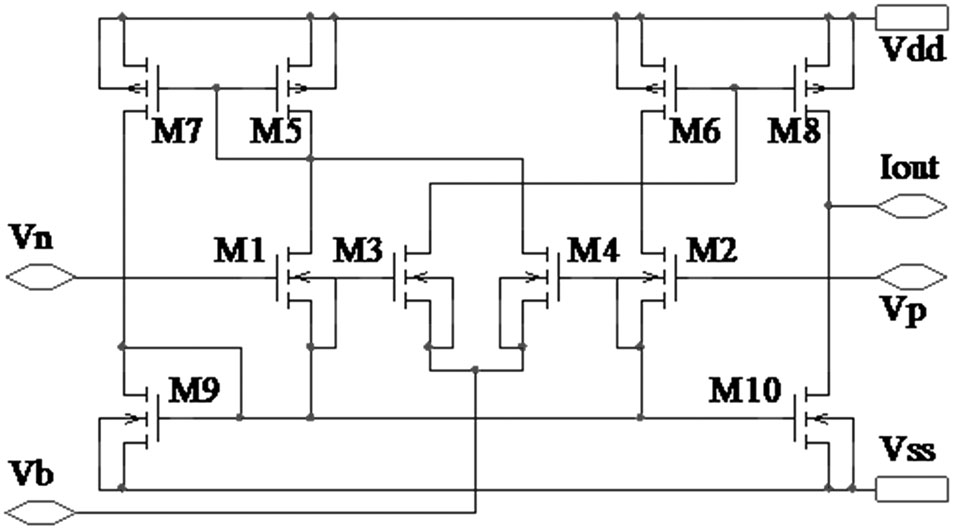
提出的内建自测方法需要对原始滤波器电路进行某些修改。所有这些修改都可以通过在原始滤波器电路中插入MOS晶体管开关来实现。在模拟电路设计领域，通过在金属化走线连接中插入MOS开关来断开环路并不是一件简单的事情。因此，MOS开关晶体管是OBT中的关键组件，并提供了OTA‐C滤波器的可测结构。

开关的特性直接影响被测滤波器的精度和功能。开关晶体管最重要的特性是导通电阻、关断电阻以及寄生电容器的值。MOS晶体管的串联电阻比金属走线的电阻大几个数量级。同样，开关的电容也比金属走线的电容高出许多倍。工作在线性区的MOS晶体管的有效电阻可表示为[22]：

$$
R_{DS} = \frac{L}{kW(V_{GS} - V_T)} \quad (15)
$$

较大的宽长比会减小串联电阻。然而，寄生电容大致与宽度和长度的乘积成正比。因此，在信号路径中选择最优的宽长比以及合理的开关插入位置，将确保对滤波器性能的影响最小。

改进的滤波器电路需要两种类型的开关：信号路径中的开关和反馈路径中的开关，以建立振荡条件。信号路径中的开关采用具有最小导通电阻的MOS晶体管实现，而所有其他开关则设计为最小尺寸。

所有仿真均在模拟环境中使用7级PSPICE仿真器进行，以验证提出的内建自测方法。结果证实，通过上述章节中描述的电路改进，实现了自启动和持续振荡。仿真结果还证实，对于每种类型的滤波器，两个正交级均被转换为振荡器，并产生接近相应滤波器级截止频率的无故障振荡频率。修改后的四阶低通滤波器在滤波器工作模式和测试工作模式下的幅频响应，以及每个双二次级的截止频率和振荡频率的详细数据如表II所示。

表I. 四阶级联、IFLF和LF滤波器的电路电容
滤波器类型	C1	C2	C3	C4
级联	2.07皮法	3.54皮法	5 pF	1.47皮法
IFLF	7.07皮法	3.54皮法	2.07皮法	1.04皮法
LF	4.14皮法	4.27皮法	2.93皮法	1.04皮法

IFLF，逆向随动反馈；LF，跃蛙。

表II. 可测四阶滤波器在测试条件下的交流（AC）响应
类型/模式	级联		IFLF		LF
	f osc	Vout	f osc	Vout	f osc	Vout
滤波器	48兆赫	0 dB	50兆赫	0 dB	50.6兆赫	0 dB
双二次级1	35兆赫	1.12伏	63兆赫	1.4伏特	48.3兆赫	1.31伏特
双二次级2	35兆赫	1.2伏特	21.3兆赫	1.04伏特	24.7兆赫	1.04伏特

IFLF，逆向随动反馈；LF，跃蛙。

表II中的仿真结果表明，用于滤波器分解并带有MOS开关的四阶级联OTA‐C滤波器的截止频率低于原始滤波器，而IFLF滤波器和LF滤波器的截止频率与原始截止频率相近。该级联滤波器在信号路径中增加了用于将滤波器划分为两个双二次级的MOS开关；因此，开关的导通电阻和寄生电容会影响滤波器两个级联级之间的阻抗匹配。由于模拟多路复用器开关的导通电阻和寄生电容以及正反馈回路中额外OTA的影响，各类滤波器的双二次级的振荡频率均低于各自的截止频率。

为了量化OBT方法对高阶OTA‐C滤波器的故障覆盖率和效率，将多种不同的灾难性故障和参数性故障注入到原始滤波器电路中，使用[15]中讨论的故障建模方法。测量了每个待测滤波器级的振荡频率，并计算其相对于相应级无故障频率的频率偏差。通过蒙特卡罗分析，确定了元件参数容差为5%时参数故障的不可检测容差带。蒙特卡罗分析表明，双二次级的频率偏差下限和上限分别约为‐2.5%和4.5%。

参数偏差从 ±10%到 ±50%引起的参数故障的完整列表分别在表III、IV和V中给出，对应于四阶级联、IFLF和LFOTA‐C滤波器。

表III. 四阶级联跨导运算放大器‐C滤波器中的参数故障检测。
元件	偏差 (%)	级联滤波器	振荡器第一级		振荡器第二级
		fosc (Hz)	Vout (V)	Δfo/fo (%)	fosc (Hz)	Vout (V)
C1和 C3	-50	4.60E+07	0.93	31.427	4.62E+07	1.31
	-40	4.30E+07	0.98	22.857	4.30E+07	1.28
	-30	4.04E+07	1.03	15.429	4.05E+07	1.25
	-20	3.83E+07	1.06	9.4286	3.84E+07	1.23
	-10	3.66E+07	1.09	4.5714	3.66E+07	1.21
	10	3.38E+07	1.11	-3.429	3.37E+07	1.18
	20	3.27E+07	1.12	-6.572	3.25E+07	1.16
	30	3.17E+07	1.12	-9.428	3.14E+07	1.16
	40	3.08E+07	1.12	-12.00	3.04E+07	1.14
	50	2.99E+07	1.12	-14.57	2.95E+07	1.13
C2和 C4	-50	4.32E+07	1.30	23.429	4.53E+07	1.24
	-40	4.11E+07	1.27	17.429	4.25E+07	1.22
	-30	3.93E+07	1.23	12.286	4.01E+07	1.22
	-20	3.77E+07	1.19	7.7143	3.82E+07	1.20
	-10	3.62E+07	1.15	3.4287	3.65E+07	1.20
	10	3.39E+07	1.07	-3.143	3.39E+07	1.19
	20	3.29E+07	1.02	-6.00	3.28E+07	1.18
	30	3.19E+07	0.98	-8.857	3.19E+07	1.17
	40	3.11E+07	0.94	-11.14	3.11E+07	1.16
	50	3.03E+07	0.90	-13.43	3.03E+07	1.16
All cap	-50	5.63E+07	1.26	60.86	5.77E+07	1.40
	-40	5.03E+07	1.23	43.71	5.10E+07	1.30
	-30	4.53E+07	1.20	29.43	4.58E+07	1.28
	-20	4.13E+07	1.17	18.00	4.15E+07	1.25
	-10	3.79E+07	1.14	8.286	3.80E+07	1.22
	10	3.26E+07	1.08	-6.861	3.26E+07	1.18
	20	3.05E+07	1.05	-12.85	3.05E+07	1.15
	30	2.86E+07	1.01	-18.29	2.86E+07	1.13
	40	2.69E+07	0.99	-23.14	2.69E+07	1.12
	50	2.55E+07	0.96	-27.14	2.55E+07	1.10
gm	-50	2.10E+07	0.50	-40.00	2.10E+07	0.74
	-40	2.44E+07	0.78	-30.29	2.41E+07	1.02
	-30	2.70E+07	0.99	-22.86	2.69E+07	1.17
	-20	2.98E+07	1.09	-14.86	2.98E+07	1.21
	-10	3.25E+07	1.11	-7.143	3.25E+07	1.21
	10	3.76E+07	1.09	7.429	3.75E+07	1.18
	20	3.99E+07	1.08	14.00	3.97E+07	1.17
	30	4.20E+07	1.06	20.00	4.16E+07	1.16
	40	4.39E+07	1.04	25.43	4.32E+07	1.16
	50	4.55E+07	1.02	30.00	4.44E+07	1.15

表IV. 四阶IFLF OTA‐C滤波器中的参数故障检测。
元件	偏差 (%)	IFLF滤波器	振荡器第一级		振荡器第二级
		fosc (Hz)	Vout (V)	Δfo/fo (%)	fosc (Hz)	Vout (V)
C1和 C3	-50	7.83E+07	1.50	24.2857	2.86E+07	1.11
	-40	7.42E+07	1.47	17.7778	2.65E+07	1.09
	-30	7.07E+07	1.43	12.2222	2.48E+07	1.07
	-20	6.78E+07	1.44	7.61905	2.35E+07	1.06
	-10	6.53E+07	1.41	3.65079	2.23E+07	1.05
	10	6.11E+07	1.40	-3.0159	2.04E+07	1.03
	20	5.92E+07	1.38	-6.0318	1.96E+07	1.02
	30	5.76E+07	1.34	-8.5714	1.89E+07	1.01
	40	5.61E+07	1.34	-10.952	1.83E+07	1.00
	50	5.47E+07	1.33	-13.175	1.77E+07	1.00
C2和 C4	-50	7.14E+07	1.42	13.3333	2.79E+07	1.12
	-40	6.95E+07	1.41	10.3175	2.61E+07	1.10
	-30	6.77E+07	1.41	7.4603	2.46E+07	1.09
	-20	6.61E+07	1.39	4.9206	2.33E+07	1.07
	-10	6.45E+07	1.39	2.3809	2.20E+07	1.05
	10	6.18E+07	1.39	-1.9047	2.04E+07	1.04
	20	6.05E+07	1.40	-3.9683	1.97E+07	1.02
	30	5.94E+07	1.38	-5.7143	1.90E+07	0.99
	40	5.83E+07	1.37	-7.4603	1.85E+07	0.97
	50	5.73E+07	1.36	-9.0476	1.79E+07	0.95
All cap	-50	8.80E+07	1.5	39.6825	3.73E+07	1.2
	-40	8.13E+07	1.5	29.0476	3.24E+07	1.17
	-30	7.57E+07	1.48	20.1587	2.87E+07	1.13
	-20	7.09E+07	1.44	12.5397	2.57E+07	1.10
	-10	6.67E+07	1.40	5.8730	2.33E+07	1.07
	10	5.97E+07	1.37	-5.2381	1.96E+07	1.01
	20	5.67E+07	1.35	-10.000	1.81E+07	0.99
	30	5.40E+07	1.33	-14.286	1.69E+07	0.97
	40	5.16E+07	1.31	-18.100	1.58E+07	0.95
	50	4.94E+07	1.30	-21.587	1.49E+07	0.94
gm	-50	4.06E+07	1.44	-35.51	1.21E+07	0.4
	-40	4.58E+07	1.50	-27.30	1.42E+07	0.61
	-30	5.07E+07	1.57	-19.52	1.61E+07	0.81
	-20	5.52E+07	1.47	-12.38	1.78E+07	0.95
	-10	5.94E+07	1.45	-5.715	1.96E+07	1.02
	10	6.65E+07	1.39	5.556	2.29E+07	1.04
	20	6.93E+07	1.38	10.00	2.45E+07	1.03
	30	7.16E+07	1.37	13.66	2.59E+07	1.03
	40	7.31E+07	1.34	16.03	2.72E+07	1.03
	50	7.40E+07	1.32	17.46	2.83E+07	1.02

OTA‐C，运算跨导电容；IFLF，逆向随动反馈。

表V. 四阶低通滤波器OTA‐C中的参数故障检测。
元件	偏差 (%)	低通滤波器滤波器	振荡器第一级		振荡器第二级
		fosc (Hz)	Vout (V)	Δfo/fo (%)	fosc (Hz)	Vout (V)
C1和 C3	-50	6.13E+07	1.43	26.915	3.29E+07	1.00
	-40	5.77E+07	1.38	19.462	3.05E+07	1.03
	-30	5.48E+07	1.35	13.456	2.87E+07	1.04
	-20	5.24E+07	1.35	8.4886	2.71E+07	1.05
	-10	5.02E+07	1.32	3.9337	2.58E+07	1.04
	10	4.66E+07	1.29	-3.520	2.38E+07	1.03
	20	4.51E+07	1.28	-6.625	2.29E+07	1.03
	30	4.37E+07	1.26	-9.524	2.21E+07	1.02
	40	4.25E+07	1.25	-12.01	2.14E+07	1.02
	50	4.13E+07	1.23	-14.50	2.08E+07	1.01
C2和 C4	-50	5.75E+07	1.34	19.047	3.26E+07	1.11
	-40	5.53E+07	1.33	14.493	3.04E+07	1.15
	-30	5.32E+07	1.32	10.145	2.86E+07	1.13
	-20	5.14E+07	1.33	6.4185	2.71E+07	1.10
	-10	4.98E+07