90纳米Gm-C滤波器设计

基于90纳米CMOS的具有新型自动调谐电路的四阶低通Gm‐C滤波器的设计与仿真

1 引言

Gm‐C滤波器适用于具有中等线性度的高频应用。由于这些滤波器中没有反馈，因此不存在稳定性问题，并且它们的功耗较低，因为可以通过最少的元件进行调谐。然而，在Gm‐C滤波器中，跨导器的开环操作特性导致电路中的输入信号较大，因此基于跨导器的滤波器的线性化非常重要。文献中已提出了多种方法来提高跨导器的线性度。这些方法包括保持输入晶体管的栅源电压之和恒定、使用浮栅晶体管、源极退化、输入电压分压器、非线性抵消、反馈放大器等。[1–9]

运算跨导放大器的一个应用是在Gm‐C滤波器的实现中。为了提高跨导放大器的低功耗性能，已采用伪差分放大器[10–12],体驱动[13, 14],电流模电路[15, 16],弱反型[17]和浮栅晶体管[18]等方法。

一种实现低压跨导放大器的技术使用CMOS反相器。在该技术中，如果N型金属氧化物半导体和P型金属氧化物半导体晶体管处于饱和区，则CMOS反相器可用作电压‐电流转换器[4]。该设计工作于AB类，但由于其伪差分结构，需要共模反馈（CMFB）和共模前馈（CMFF）电路。连续时间低通滤波器已广泛应用于无线通信系统和硬盘驱动器等宽带应用中。本文首先提出了一种基于CMOS反相器的可调跨导放大器，然后提出了一种截止频率为1吉赫兹并带有自动调谐电路的Gm‐C滤波器。第2节介绍了提出的OTA。第3节解释了Gm‐C滤波器和自动调谐电路的结构。第4节给出了仿真和版图后仿真结果，第5节总结了全文。

2 提出的基于CMOS反相器的可调跨导放大器

所提出的可调放大器的结构如图1所示。该伪差分电路包含四个部分，即输入反相器、增益增强器（负阻）、CMFF和共模反馈。该电路为单级结构，因此没有寄生零点和极点，能够在高频下工作。晶体管的共模电压值为电源电压的一半，所有晶体管均工作在饱和区。

晶体管M1‐2和M3‐4产生跨导。CMOS反相器具有良好的线性度，由于其伪差分结构，适用于低压应用。

为了最大化差分增益，在输出节点处将晶体管M5‐6和M9‐10交叉耦合，以产生负阻并提高差分模式下的输出阻抗。由于电路参数取决于晶体管的寄生电阻和跨导，这些参数会因失配或温度变化而发生变化。在[10]和[11],中，通过控制晶体管的体电压来调谐电路。在这些参考文献中，N型金属氧化物半导体和P型金属氧化物半导体晶体管的体电压以相反方向变化，从而使晶体管的阈值电压发生变化，并可控制跨导值。

在本研究中，提出了一种新的设计，通过改变负阻结构，利用晶体管M5‐6和M9‐10在输出节点处的负阻变化来实现电路调谐。调谐电压Vt施加到晶体管M25的栅极。当Vt变化时，电压Vp和Vn朝相反方向变化。其中，Vp施加到晶体管M8和M12的栅极，Vn施加到晶体管M7和M11的栅极。因此，来自晶体管M5‐6和M9‐10的负阻值发生变化，从而实现电路的调谐。与[11],中的方法相比，本方法的优点在于电路不是通过体电压进行调谐，因此不存在漏电流和闩锁问题。此外，所提出的方法可在标准互补金属氧化物半导体工艺中实现。

为了降低共模增益，该放大器采用了CMFF和共模反馈电路。实际上，这些电路被集成在一起以减小整体尺寸和功耗[11]。在此运算跨导放大器中，所提出的共模反馈电路将输出共模电压稳定在VDD/2附近。

本文中的共模反馈电路结构（晶体管M21‐22和M13‐18）与参考文献[11]中的电路不同。测量输出共模电压的电阻被晶体管取代，因此在共模反馈环中省去了一个反相器；即电路的尺寸减小，集成能力增强。

此处，在连接M21‐22漏极的节点上，仅输出共模电流产生后，M24栅极处的电压与M23栅极处的参考电压（VDD/2）进行比较。随后，电流的变化改变了节点A处的电压，从而使反相器M13‐16减小输出共模电压的变化。CMFF通过使用晶体管M17‐20和反相器M13‐16实现。由于晶体管M17‐20充当负单位增益放大器，反相器M13‐16可防止输出端的共模电流流动以及运算跨导放大器的非线性。

由于CMFF电路的增益小于1，因此无需担心其不稳定性。然而，有必要研究CMFB电路的稳定性，可通过开环CMFB电路的相位裕度仿真进行评估。

CMFB环路有两个极点。主导极点位于2gm5/CL，非主导极点位于gm17?gm18/CA；注意，CL和CA分别为负载电容和节点A处看到的电容。开环增益等于g2 m1r o1=4gm5。通过对CMFB电路进行开环仿真，并考虑该滤波器设计中负载电容为200 fF，仿真得到的相位裕度为 57°，出现在1.88 GHz（图2），这确保了环路的稳定性。

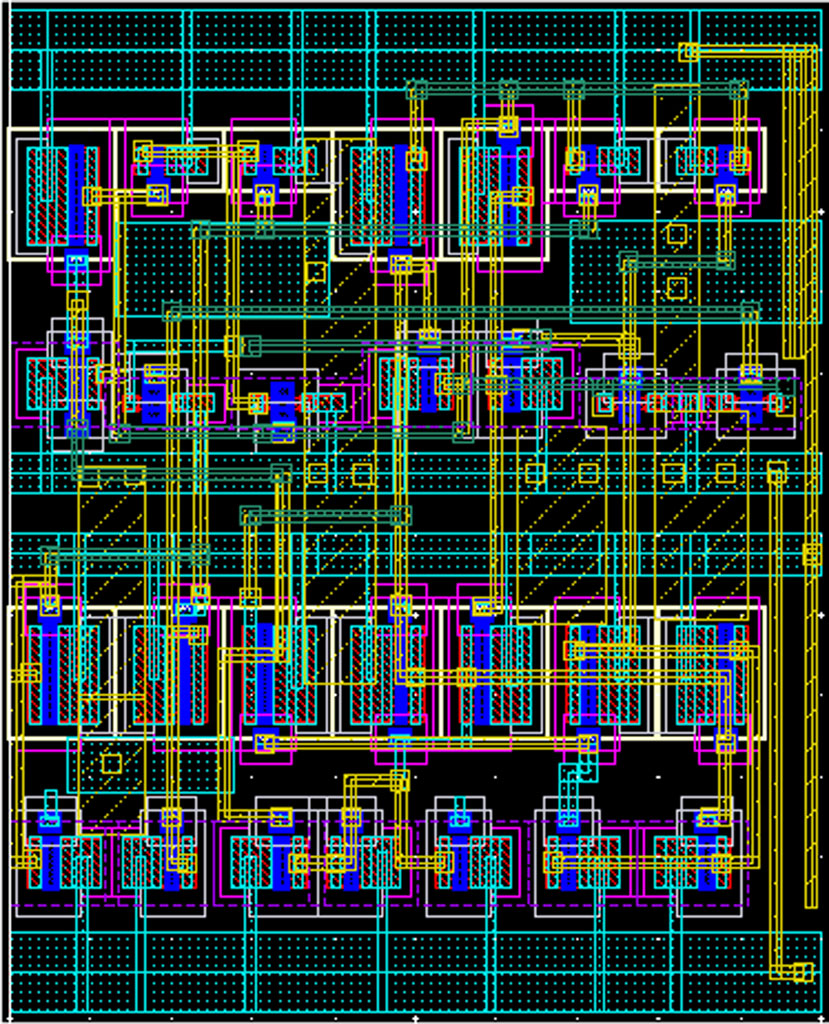
表1 电路晶体管的尺寸
| WN/LN[nm/nm] | WP/LP[nm/nm] |
| — | — |
| M5, M7, M9, M11 | 120/200 – |
| M6、M8、M10、M12 | – 315/100 |
| 其他 | 600/120 1180/100 |

由M5‐12产生的差模和共模电阻为：
$$
R_{diff} = r_{o5} \parallel r_{o7} \parallel \frac{1}{g_{m5}}, \quad R_{cm} = \frac{1}{2} r_{o5} \parallel r_{o7} \parallel \frac{1}{g_{m5}}
\quad (1)
$$

如果该电路以容性阻抗作为负载，并假设MOS满足二次方程，则运算跨导放大器的共模与差模电流相等：
$$
i_{oc} = \frac{6g_{m1}}{3 + g_{m1}r_{o1}} \cdot \frac{1}{1 + g^2_{m1}r_{o1}} \cdot \frac{1}{1 + (4g_{d1} + 2g_{d5} + 2g_{d7} + 2g_{m5})/xC} v_{ic}
\quad (2)
$$

and
$$
i_{od} = \frac{2g_{m1}}{1 + (4g_{d1} + 2g_{d5} + 2g_{d7} - 2g_{m5})/xC} v_{id}
\quad (3)
$$

其中，$g_m$ 是晶体管的跨导，$g_d$ 是晶体管的漏源寄生跨导。该电路的差模跨导和共模跨导可通过以下公式得到：
$$
G_{mc} \approx
\begin{cases}
0 & x \to 0 \
6(g_{m1}r_{o1}) & x \to 1
\end{cases}
\quad (4)
$$

$$
G_{md} \approx 2g_{m1}
\quad (5)
$$

根据式(4)可知，共模增益在所有频率下均较低，且不依赖于负载阻抗。

3 低通滤波器结构和自动调谐电路

四阶等波纹线性相位可调Gm‐C滤波器的框图如图3所示。该设计通过级联两个二阶滤波器[11]实现。这些晶体管的尺寸与表1中所示跨导晶体管的尺寸相同。

由于该电路中的跨导器是级联的，因此共模反馈电路不需要专用的共模电压检测器，因为输出共模电压的值（带负号）是从下一级的共模前馈电路中提取的。因此，通过集成共模反馈和共模前馈电路，每个滤波器级可以减少两个晶体管。从图3可以看出，仅需四个共模反馈电路即可稳定输出共模电平。

3.1 频率调谐系统

由于滤波器截止频率取决于gm/碳值，它会随温度和工艺的变化而变化。因此，为了精确控制滤波器操作，采用了一种新的片上自动控制电路，为简便起见，其单端框图如图4所示。该调谐电路仅由反相器和运算跨导放大器组成。该电路的优点在于，它在电流模式下进行比较，无需使用[10, 19],中的峰值检测电路，因此复杂度更低，占用更少的芯片面积。此外，本文中频率自动调谐电路的结构与参考文献[11]中的电路不同。在此电路中，参考频率可通过g mb gma（跨导Ib与 Ia之比）降低。

该调谐电路在低于运算跨导放大器单位增益频率的频率下工作，与[11],相比，具有在选择参考时的灵活性优势频率，更精确的积分器，从而实现更精确的调谐。

在此图中，OTAx 提供了与滤波器中使用的 OTA 类似的版本，碳L创建了类似的负载条件。积分器的单位增益频率获取如下：
$$
f_u = \frac{G_{mx}}{2\pi C_L}
\quad (6)
$$

其中$G_{mx}$是OTAx的小信号跨导。通过使用具有参考频率$f_{ref}$的参考信号，该参考频率由
$$
V_{ref} = V_m \sin(2\pi f_{ref} t)
\quad (7)
$$

电流 i1 和 i2 获得如下：
$$
i_1 = \left(\frac{f_u}{f_{ref}}\right)^2 \cdot 2g_{ma}V_m \sin(2\pi f_{ref} t)
\quad (8)
$$

$$
i_2 = \left(\frac{g_{mb}}{g_{ma}}\right)^2 \cdot 2g_{ma}V_m \sin(2\pi f_{ref} t)
\quad (9)
$$

电流i1和i2分别与积分器的单位增益频率与参考频率之比以及Ib与Ia跨导之比成正比。因此，通过比较输出节点处的i1和i2电流，得到一个校正误差（控制信号），并将其应用于闭环系统中的OTAx，以最小化误差值。该控制信号还被施加到滤波器的所有从属跨导器上，使其频率被调谐。

基于90纳米CMOS的具有新型自动调谐电路的四阶低通Gm‐C滤波器的设计与仿真（续）

4 仿真结果

为了评估跨导器和设计的滤波器的性能，使用 Cadence软件、台积电90纳米CMOS技术和1伏电源电压对电路进行仿真。

当具有0.5伏特共模电压的差分信号施加到跨导器输入端时，获得无负载情况下的仿真频率响应，如图5所示。根据该图，在低频下，跨导器的开环差分直流增益为34分贝，其-3 dB截止频率和单位增益频率分别为200兆赫兹和10吉赫。此外，提出的OTA具有87°的相位裕度；该较高的相位裕度值可确保交流稳定性。

当向OTA施加共模输入时，电路的频率响应如图6所示。实际上，共模增益在频率达到约1吉赫兹范围内约为-26分贝。

图7展示了运算跨导放大器的跨导。从该图可以看出，电路的差分跨导（Gmd）为0.74毫西门子，且跨导在高达4吉赫兹时仅有轻微偏差。

为了确定运算跨导放大器的输出1分贝压缩点（这是一个与三阶截取点IP3同样关键的线性度指标），在100兆赫兹下进行了输出功率与输入功率的仿真。输出功率Po与输入功率Pin的关系曲线如图8所示，显示输出P 1dB 为-10分贝毫瓦。

进行了双音测试以模拟运算跨导放大器的互调失真并确定其三阶截取点。输入音调为96兆赫兹和100兆赫兹，结果如图9所示。该图显示输入三阶截取点为-1 dBm。图10显示了运算跨导放大器的版图设计；如图所示，运算跨导放大器占有的面积为0.010 × 0.012 mm²。

图11显示了低通滤波器的频率响应。该滤波器的截止频率为1 GHz。滤波器和调谐电路的总功耗为3.7毫瓦；其中调谐电路本身消耗0.6毫瓦，约占滤波器总功耗的16.3%。本文通过仿真三阶互调分量来评估线性度。当施加幅度为200毫伏峰峰值（-22 dBm）的双音输入信号时，在1 GHz处（即接近滤波器的截止频率）的IM3值为-37分贝（图12）。图13显示了滤波器的群延迟。结果表明，在最高达1.3吉赫兹（即滤波器截止频率的1.3倍）的频率范围内，群延迟的总体变化小于6%。

滤波器的输入参考电压噪声谱密度如图14所示。在5兆赫和10兆赫时（当滤波器增益约为0分贝时），分别等于150和89 nV/√Hz。

为了评估所提出的滤波器在工艺误差下的性能，采用了蒙特卡洛仿真。根据图15，滤波器截止频率的蒙特卡洛仿真的均值和标准差分别为1吉赫和39.4兆赫（50次迭代）。由滤波器蒙特卡洛频率响应仿真（图16）可知，该电路在工艺误差下变化不大。

图17显示了该滤波器的设计与版图，其占用面积为0.040 × 0.023 mm²。

5 结论

基于CMOS反相器的可调谐运算跨导放大器使用台积电90纳米技术和1伏电源电压进行了设计和仿真。在该高频OTA中，提出的共模反馈电路与共模前馈电路相结合，通过调节由正反馈产生的负阻来调谐跨导。该提出的OTA用于设计截止频率为1吉赫兹的低通Gm‐C滤波器。此外，还提出了一种自动调谐电路以实现精确的滤波器操作。仿真结果显示，该OTA的差分直流增益、共模增益、单位增益频率和相位裕度分别为34分贝、-26分贝、10吉赫和87度。此外，该滤波器的功耗为3.7毫瓦，在截止频率处的三阶互调失真为-37分贝，群延迟变化小于6%可达1.3 fc。而且，蒙特卡洛仿真表明所提出的滤波器对工艺误差具有良好的鲁棒性。

表2 比较最近发布的滤波器的性能
| 项目 | 本工作 | [20] | [11] | [10] |
| — | — | — | — | — |
| 技术 | 90纳米CMOS | 28纳米FD-SOI CMOS | 90纳米CMOS | 180纳米CMOS |
| 滤波器阶数 | 4 | 3 | 4 | 4 |
| 滤波器类型 | LPF Gm-C | LPF Gm-C | LPF Gm-C | LPF Gm-C |
| $f_c$ | 1吉赫兹 | 459 MHz | 1吉赫兹 | 1吉赫兹 |
| 自动调谐 (AT) | Yes | Yes | Yes | Yes |
| IM3/HD3 | -37分贝 在 0.2VPP(IM3) | 2.4dBVP(IIP3) | -42分贝 在 0.2VPP(IM3) | -43分贝（在 0.35 伏特PP时，IM3） |
| 电源 | 1 V | 1 V | 1 V | 1.5 伏特 |
| 功耗 | 3.7毫瓦 | 5.6毫瓦 | 8mW | 175毫瓦 |
| 带内增益 | 0 dB | -0.3分贝 | 0 dB | 0 dB |
| 群延迟纹波 | <6% 在 1.3 fc | – | – | <4% 在 1.5 fc |
| 测量结果 | | 测量结果 | | *测量结果 |