Qwen代码层面解密

Instruct Model
“bos_token_id”: 151643,
“eos_token_id”: 151645, //instruct model的eos_token_id修改为<|im_end|>, base model本来都是<end_of_text>

解密1：ChatTemplate and Function Call

{%- if tools %} #是否存在工具类，在对话最开始提供
    {{- '<|im_start|>system\n' }}
    {%- if messages[0]['role'] == 'system' %}
        {{- messages[0]['content'] }}
    {%- else %}
        {{- 'You are Qwen, created by Alibaba Cloud. You are a helpful assistant.' }}
    {%- endif %}
    {{- "\n\n# Tools\n\nYou may call one or more functions to assist with the user query.\n\nYou are provided with function signatures within <tools></tools> XML tags:\n<tools>" }}
    {%- for tool in tools %}
        {{- "\n" }}
        {{- tool | tojson }}
    {%- endfor %}
    {{- "\n</tools>\n\nFor each function call, return a json object with function name and arguments within <tool_call></tool_call> XML tags:\n<tool_call>\n{\"name\": <function-name>, \"arguments\": <args-json-object>}\n</tool_call><|im_end|>\n" }}
{%- else %} #正常对话第一步走这个流程
    {%- if messages[0]['role'] == 'system' %}
        {{- '<|im_start|>system\n' + messages[0]['content'] + '<|im_end|>\n' }}
    {%- else %}
        {{- '<|im_start|>system\nYou are Qwen, created by Alibaba Cloud. You are a helpful assistant.<|im_end|>\n' }}
    {%- endif %}
{%- endif %}
{%- for message in messages %} #遍历多轮对话信息
    {%- if (message.role == "user") or (message.role == "system" and not loop.first) or (message.role == "assistant" and not message.tool_calls) %}
        {{- '<|im_start|>' + message.role + '\n' + message.content + '<|im_end|>' + '\n' }}
    {%- elif message.role == "assistant" %}
        {{- '<|im_start|>' + message.role }}
        {%- if message.content %}
            {{- '\n' + message.content }}
        {%- endif %}
        {%- for tool_call in message.tool_calls %}
            {%- if tool_call.function is defined %}
                {%- set tool_call = tool_call.function %}
            {%- endif %}
            {{- '\n<tool_call>\n{"name": "' }}
            {{- tool_call.name }}
            {{- '", "arguments": ' }}
            {{- tool_call.arguments | tojson }}
            {{- '}\n</tool_call>' }}
        {%- endfor %}
        {{- '<|im_end|>\n' }}
    {%- elif message.role == "tool" %}
        {%- if (loop.index0 == 0) or (messages[loop.index0 - 1].role != "tool") %}
            {{- '<|im_start|>user' }}
        {%- endif %}
        {{- '\n<tool_response>\n' }}
        {{- message.content }}
        {{- '\n</tool_response>' }}
        {%- if loop.last or (messages[loop.index0 + 1].role != "tool") %}
            {{- '<|im_end|>\n' }}
        {%- endif %}
    {%- endif %}
{%- endfor %}
{%- if add_generation_prompt %}  #一般需要add_generation_prompt=True，直到模型输出eos_token
    {{- '<|im_start|>assistant\n' }}
{%- endif %}

解密2: Qwen的tokenizer底层原理，word2id的映射关系

'<|im_start|>system\nYou are Qwen, created by Alibaba Cloud. You are a helpful assistant.<|im_end|>\n<|im_start|>user\nGive me a short introduction to large language model.<|im_end|>\n<|im_start|>assistant\n

['<|im_start|>', 'system', 'Ċ', 'You', 'Ġare', 'ĠQ', 'wen', ',', 'Ġcreated', 'Ġby', 'ĠAlibaba', 'ĠCloud', '.', 'ĠYou', 'Ġare', 'Ġa', 'Ġhelpful', 'Ġassistant', '.','<|im_end|>', 'Ċ', '|im_start|>', 'user', 'Ċ', 'Give', 'Ġme', 'Ġa', 'Ġshort', 'Ġintroduction', 'Ġto', 'Ġlarge', 'Ġlanguage', 'Ġmodel', '<|im_end|>','Ċ', '<|im_start|>', 'assistant', 'Ċ']

tensor([[151644,   8948,    198,   2610,    525,   1207,  16948,     11,   3465,553,  54364,  14817,     13,   1446,    525,    264,  10950,  17847,13, 151645,    198, 151644,    872,    198,  35127,    752,    264,2805,  16800,    311,   3460,   4128,   1614,     13, 151645,    198,151644,  77091,    198]])

疑问1：Ċ代表什么，似乎代表所有\n,空格等间隔符," You",“You”,"\nYou"的分词结果均不一致

tokenize分词结果解析：“i love You” [‘i’, ‘Ġlove’, ‘ĠYou’]
“i loveYou”[‘i’, ‘Ġlove’, ‘You’]
“I love\nYou”[‘I’, ‘Ġlove’, ‘Ċ’, ‘You’]
You的id为2610，而ĠYou为1446，不存在“ You”,"\nYou"的token,而分别用’Ċ’'Ġ’代替，tokenizer的分词流程和原理是什么呢？

首先tokenizer由normalizers，pre_tokenizers,model and post_tokenizers四部分组成，这部分基础可以参考huggingface-tokenizer doc

normalizer:NFC
NFC是“组合形式”（Canonical Composition），它将字符表示为其最“复合”的形式。
这意味着，如果一个字符可以通过Unicode中的组合规则由两个或更多的字符组合而成，那么在NFC中，这个字符就会被表示为一个单独的复合字符。
pre_tokenizer:Split and ByteLevel
通过Split组件，将文本分解成单词、缩写、数字和标点符号等基本单元。
通过ByteLevel组件，处理Unicode字符，确保多字节字符被正确识别。
model: ByteLevel BPE
post_processor: ByteLevel

code流程：PreTrainedTokenizer的tokenize方法会调用QwenTokenizer重写的_tokenize方法，处理BPE分词和special token的合并

解密3: tie_word_embeddings的实现

对于小参数模型，为了让中间的Decoder Layer占比提高，可以将nn.Embedding层和lm_head使用相同的权重矩阵
nn.Embedding是用于快速检索token_id->token_embedding的矩阵，形状为vocab_sizehidden_size
lm_head是token分类的预测头，形状为hidden_sizevocab_size

self.lm_head = nn.Linear(config.hidden_size, config.vocab_size, bias=False)
self.embed_tokens = nn.Embedding(config.vocab_size, config.hidden_size, self.padding_idx)

本例中vocab_size为151936，tokenizer预设了151664个，留了很多可以作下游special token 做SFT微调

在Qwen2ForCausalLM中定义：self._tie_or_clone_weights(output_embeddings, self.get_input_embeddings())
可以看到在torch下权重是浅克隆，参数更新对两头都有效

def _tie_or_clone_weights(self, output_embeddings, input_embeddings):
    """Tie or clone module weights depending of whether we are using TorchScript or not"""
    if self.config.torchscript:
        output_embeddings.weight = nn.Parameter(input_embeddings.weight.clone())
    else:
        output_embeddings.weight = input_embeddings.weight

    if getattr(output_embeddings, "bias", None) is not None:
        output_embeddings.bias.data = nn.functional.pad(
            output_embeddings.bias.data,
            (
                0,
                output_embeddings.weight.shape[0] - output_embeddings.bias.shape[0],
            ),
            "constant",
            0,
        )
    if hasattr(output_embeddings, "out_features") and hasattr(input_embeddings, "num_embeddings"):
        output_embeddings.out_features = input_embeddings.num_embeddings

解密4: Qwen2ForCausalLM的forward函数

这里对Qwen2Model基础模型的forward暂时不深入讨论

""" 入参说明
input_ids: torch.LongTensor = None,
attention_mask: Optional[torch.Tensor] = None,
position_ids: Optional[torch.LongTensor] = None, [0-n_positions-1]位置索引
past_key_values: Optional[List[torch.FloatTensor]] = None,#Pre-computed hidden-states in attention for KV cached
inputs_embeds: Optional[torch.FloatTensor] = None, #没啥用，不想用look up embedding
labels: Optional[torch.LongTensor] = None, #[0-vocab_size]或者-100的整数token_id作为label,其中-100在交叉熵损失函数中是忽略的
use_cache: Optional[bool] = None,
output_attentions: Optional[bool] = None,
output_hidden_states: Optional[bool] = None, #whether or not to return hidden of all layers
return_dict: Optional[bool] = None, #return ModelOutput class
cache_position: Optional[torch.LongTensor] = None, #position_id not affected by padding
num_logits_to_keep: int = 0, # hidden_states[:, -num_logits_to_keep:, :] 只计算最后num个token的预测结果，在生成阶段一般取1来降低显存占用
**loss_kwargs,
"""

首先Qwen2ForCausalLM调用Qwen2Model的forward函数，入参基本和上述内容一致，获得多层处理后的hidden_states

参数说明
seq_len:39, hidden_size=896, layer=24
last_hidden_state和hidden_state表示最后一层和所有层的hidden，但是这里我的output_hidden_states=False
past_key_values存放了24层Attention Block里面的Key_list, value_list, 形状为batch, n_head,n_token, d_head，list长度为24
num_logits_to_keep设置为1，只计算最后一个token的预测结果，形状为batch, 1, vocab_size

得到的BaseModelOutputWithPast包含上述内容，其中last_hidden_state通过lm_head投影得到一组logits，表示tokens的预测概率分布

如果入参中包含labels，则会计算loss用于模型训练

labels (torch.LongTensor of shape (batch_size, sequence_length), optional):
Labels for computing the masked language modeling loss. Indices should either be in [0, ..., config.vocab_size] or -100 (see input_ids docstring). Tokens with indices set to -100 are ignored (masked), the loss is only computed for the tokens with labels in [0, ..., config.vocab_size].

输入labels, input_ids->hidden_states->logits，即可采用交叉熵损失函数计算分类loss
值得注意地，在LLM的训练过程中，每个token的下一个token就是该token的标签，所以这是一种自监督损失函数，只需要确定mask attention不产生信息泄露即可训练
调用：model(input_ids=model_inputs.data['input_ids'],attention_mask = model_inputs.data['attention_mask'],labels = model_inputs.data['input_ids'])

def ForCausalLMLoss(
    logits, labels, vocab_size: int, num_items_in_batch: int = None, ignore_index: int = -100, **kwargs
):
    # Upcast to float if we need to compute the loss to avoid potential precision issues
    logits = logits.float()
    # Shift so that tokens < n predict n
    shift_logits = logits[..., :-1, :].contiguous()
    shift_labels = labels[..., 1:].contiguous()
##这两行代码将 logits 和 labels 进行平移操作。在因果语言模型中，模型需要预测下一个词，因此对于每个位置 i，模型的输入是词 i，目标是预测词 i+1。通过将 logits 和 labels 平移一位，我们可以确保模型的输出（logits）与正确的目标标签（labels）对齐。
## 这样logits保留前n-1位，labels保留后n-1位
    # Flatten the tokens
    shift_logits = shift_logits.view(-1, vocab_size)
    shift_labels = shift_labels.view(-1)
    # Enable model parallelism
    shift_labels = shift_labels.to(shift_logits.device)
    loss = fixed_cross_entropy(shift_logits, shift_labels, num_items_in_batch, ignore_index, **kwargs)
    return loss

显然labels保留了后面的n-1个，logits保留了前面的n-1个，自监督是LLM训练的基础

解密5：Qwen2网络模型结构

Qwen网络结构总览图，来自B站UP主良睦路程序员绘制的网络结构我觉得很清晰，不过UP主绘制的是LLAMA的网络，但是Qwen和LLAMA的网络结构可以说是一模一样

Qwen2 0.5B版本
Qwen2ForCausalLM(
  (model): Qwen2Model(
    (embed_tokens): Embedding(151936, 896)
    (layers): ModuleList(
      (0-23): 24 x Qwen2DecoderLayer(
        (self_attn): Qwen2Attention(
          (q_proj): Linear(in_features=896, out_features=896, bias=True)
          (k_proj): Linear(in_features=896, out_features=128, bias=True) #Group size=7
          (v_proj): Linear(in_features=896, out_features=128, bias=True)
          (o_proj): Linear(in_features=896, out_features=896, bias=False)
          (rotary_emb): Qwen2RotaryEmbedding()
        )
        (mlp): Qwen2MLP(
          (gate_proj): Linear(in_features=896, out_features=4864, bias=False)
          (up_proj): Linear(in_features=896, out_features=4864, bias=False)
          (down_proj): Linear(in_features=4864, out_features=896, bias=False)
          (act_fn): SiLU()
        )
        (input_layernorm): Qwen2RMSNorm((896,), eps=1e-06)
        (post_attention_layernorm): Qwen2RMSNorm((896,), eps=1e-06)
      )
    )
    (norm): Qwen2RMSNorm((896,), eps=1e-06)
    (rotary_emb): Qwen2RotaryEmbedding()
  )
  (lm_head): Linear(in_features=896, out_features=151936, bias=False)
)

解密6： Qwen2RotaryEmbedding()细节原理

首先提一下苏剑林博客的正余弦绝对位置编码的基础概念

容易看出，对于不同的token position k, 存在一个正余弦交替的位置编码向量代表这个token的绝对位置信息；使用正余弦交替具备一定的推导规律和[-1,1]的上下界，在早期比较常用；
疑惑1：
$div\_term=10000^{-2i/d}\ast k$代表什么，base选择10000的好处在哪里？
首先$10000^{-2i/d}$随着位置编码维度的趋近于$d/2$，这个负幂指数函数是单调递减的，例如d_model=512时，结果如下：

即$sin(k\ast div\_term)$或$cos(k\ast div\_term)$都是一个开始变化大，结尾变化小（低维高频、高频低维）的编码分布，如k=10的位置编码结果如下：

k=300的位置编码结果如下：

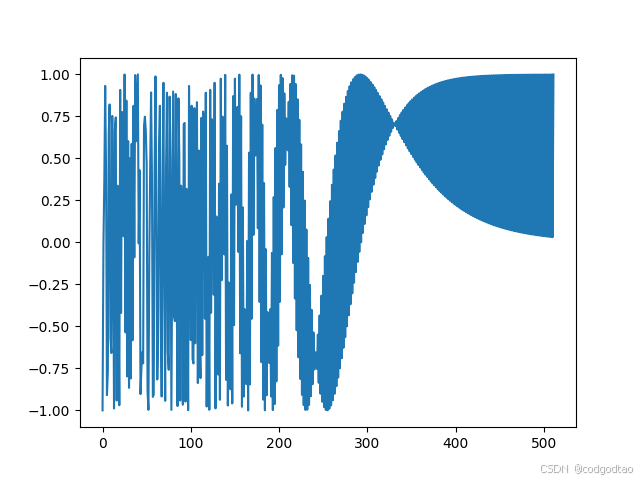
可以看到这种正余弦位置编码具备良好的数据范围，编码的向量存在低维高频、高维低频的信息分布；接下来分析位置编码的“远程衰减性”，即位置编码内积运算的结果应该和toknes之间的距离负相关，越远的tokens位置编码相似度越低，在Transformer中可以让模型更多关注“局部注意力”；
下图为k=1的位置编码与k=2-500位置编码的内积运算结果，显然满足远程衰减性质

综上，回顾刚刚提出的$10000^{-2i/d}$中base=10000的原因，其实主要是长度覆盖范围的问题，base过低如等于100时，

曲线明显更加平滑了，原来k=10的位置编码如下：

每个位置的位置编码的波长变得更加平滑，不同位置的位置编码间，波长差异明显减小了；在通过选择较大的base可以保证不同位置之间的波长差异足够大，从而使得即使是在很长的序列中，相邻位置也能有明显的区别。这样做的目的是为了确保模型能够区分出不同位置的token，即使它们相隔很远。
比较大的base，$bas{e}^{-2i/d}$曲线比较sharp，可以防止短周期内出现重复的位置信息，从而保障了长度衰减能力，base=100的时候，长度衰减能力很快就会失效，因为sin cos的周期性在相邻区间产生了相似的位置编码

# sincos位置编码的简单实现
class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout=0.1, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange( #0-d/2-1范围的， 0,2,4,6...的2i或2i+1维度分量的div_term
            0, d_model, 2).float() * (-math.log(base) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term) #max_len, d_model//2 一次赋值所有sin的内容
        pe[:, 1::2] = torch.cos(position * div_term) #max_len, d_model//2 一次赋值所有cos的内容
        pe = pe.unsqueeze(0).transpose(0, 1) #max_len, 1, d_model
        self.register_buffer('pe', pe)

    def forward(self, x):
        """
        x: [seq_len, batch_size, d_model]
        """
        x = x + self.pe[:x.size(0), :]
        return self.dropout(x)

Rope的原理

复数是数学中一种基本的数类型，它们由实数和虚数单位 ( i ) 组成，其中 ( i ) 定义为 ( i^2 = -1 )。一个复数通常写作 ( a + bi )，这里 ( a ) 和 ( b ) 是实数，( a ) 被称为复数的实部，而 ( b ) 被称为复数的虚部。

一个复数表示$e^{i\theta }$，基于欧拉公式可以得到其相应的旋转坐标表示

基于上述有关复数、极坐标和欧拉公式的概念，我们可以简单推导Rope的原理了（证明过程请见苏神博客）

1. 定义目标

对于二维向量$q=(q_0,q_1)$,$k=(k_0,k_1)$，我们希望定义一个位置编码函数，能够表示$f(q,m)$,$f(k,n)$后，$q,k$的向量内积（Attention）运算后能够表示$m-n$的相对位置关系
即求解满足$<f(q,m),f(k,n)>=g(q,k,m-n)$的$f$的一个解

我们知道向量内积运算结果满足以下定义
$<q,k>=q_0\ast k_0+q_1\ast k_1=Re[q{k}^{\ast }]$,其中$k^{\ast }$是复数域上k的共轭复数，即$k_0-i{k}_1$，根据复数乘法运算规律可以知道$q{k}^{\ast }$的实数域部分和向量内积的相等性；

因此上式求解等同
$<f(q,m),f(k,n)>=g(q,k,m-n)=Re[f_q{f}_k^{\ast }]$，通过假设$f(q,0)=q,f(k,0)=k$
求解$<f(q,m),f(k,n)>=f_q{f}_k^{\ast }=G(q,k,m-n)$,这里假设存在一个复数$G(q,k,m-n)$,其实数域等于$g(q,k,m-n)$
在复数域的极坐标上得到方程组
$$\begin{array}{rl}\mathbf{f}(\mathbf{q},m)& =R_f(\mathbf{q},m)e^{\text{i}{\Theta }_f(\mathbf{q},m)}\\ \mathbf{f}(\mathbf{k},n)& =R_f(\mathbf{k},n)e^{\text{i}{\Theta }_f(\mathbf{k},n)}\\ \mathbf{G}(\mathbf{q},\mathbf{k},m-n)& =R_G(\mathbf{q},\mathbf{k},m-n)e^{\text{i}{\Theta }_G(\mathbf{q},\mathbf{k},m-n)}\end{array}$$
2. Rope定义
上述方程组的一个解可以是$f(q,m)=||q||e^{\text{i}({\theta }_q+m\theta )}=q{e}^{im\theta }$，第二个等号成立因为这就是极坐标旋转的几何含义，||q||是q的模长，$m\theta$是q逆时针旋转的幅角度
验证一下
$$\begin{array}{rl}\mathbf{f}(\mathbf{q},m)& =q{e}^{im\theta }\\ \mathbf{f}(\mathbf{k},n)& =k{e}^{in\theta }\\ \mathbf{G}(\mathbf{q},\mathbf{k},m-n)=f(q,m)f(k,n{)}^{\ast }& =q{e}^{im\theta }k{e}^{-in\theta }=qk{e}^{i(m-n)\theta }\end{array}$$
即$f(q,m)$实现了绝对位置建模的同时，以向量内积的方式建模了相对距离m-n!!!

3. Rope实现
   $f(q,m)=||q||e^{\text{i}({\theta }_q+m\theta )}=q{e}^{im\theta }$，可以很容易基于欧拉公式得到，$e^{im\theta }$可以表示为复数$cosm\theta +isinm\theta$，通过复数的运算原理，$q{e}^{im\theta }$等价于旋转矩阵与向量q的相乘，而这也是复数运算的几何意义，该变换实际上对应着向量的旋转；
   $$\mathbf{f}(\mathbf{q},m)=\left(\begin{array}{cc}\cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{array}\right)\left(\begin{array}{c}{q}_0\\ q_1\end{array}\right)=R_{m}q$$
   
   内积线性叠加性：内积是线性的，可以分解为多个部分的内积之和。
   二维到n维的扩展：通过将高维向量分解为多个二维向量，并对每个二维向量应用相同的旋转矩阵。
   不同的 $\theta$：代表不同维度上的旋转角度，确保每个二维子空间独立旋转,这个原理类似之前的sincos位置编码中，对每个位置m的位置编码，不同维度有类似的设计，应该是为了增加不同位置之间的波长差异，防止在较远的position出现相似的位置编码造成远程衰减的失效。

# easy code for Rope
由于R_m的稀疏性，可以将其分解为sin,cos两个部分，与整理后的q进行逐元素*实现上述旋转位置编码
inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2, dtype=torch.int64).float().to(device) / dim))
#inv_freq 代表 theta，即10000^{-2i/d_model}， 从公式可以看到只需要一半，即i从[0-d/2-1]进行取值
freqs = (inv_freq_expanded.float() @ position_ids_expanded.float()).transpose(1, 2)
# m*theta, inv_freq*position ，每个position计算一个位置编码
emb = torch.cat((freqs, freqs), dim=-1)
#这里复制了一份，匹配q,k的长度，因为freqs 目前只有一半，这种复制直接在后面添加
 cos = emb.cos()
sin = emb.sin()

def rotate_half(x):
    """将后面一半元素反转到前面，并取负数"""
    x1 = x[..., : x.shape[-1] // 2]
    x2 = x[..., x.shape[-1] // 2:]
    return torch.cat((-x2, x1), dim=-1)

q_embed = (q * cos) + (rotate_half(q) * sin)
 k_embed = (k * cos) + (rotate_half(k) * sin)

从Qwen的代码看，与上文提到的两个元素一组进行翻转的公式不太一样了，以q为例子，真实的代码计算结果为：

这是一种高效的代码实现，不过是将向量q视为两部分，以类似二维向量旋转的公式来处理N维，将一半的元素视为一个整体元素进行翻转，二维情况的实现如下：
$$\mathbf{f}(\mathbf{q},m)=\left(\begin{array}{cc}\cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{array}\right)\left(\begin{array}{c}{q}_0\\ q_1\end{array}\right)=\left(\begin{array}{c}cosm\theta \\ cosm\theta \end{array}\right)\ast \left(\begin{array}{c}{q}_0\\ q_1\end{array}\right)+\left(\begin{array}{c}sinm\theta \\ sinm\theta \end{array}\right)\ast \left(\begin{array}{c}-q_1\\ q_0\end{array}\right)$$

进一步地，旋转位置编码如何拓展到视觉场景Rope 2D，为了让patch的Embeding包含位置(x,y)的信息，可以采用以下方式，与1D的情况相比，位置编码的一半维度用于表示x，一半表示y,$\theta$取0-d/4-1即可
$${\mathcal{R}}_{x,y}=\left(\begin{array}{cccc}\cos x\theta & -\sin x\theta & 0& 0\\ \sin x\theta & \cos x\theta & 0& 0\\ 0& 0& \cos y\theta & -\sin y\theta \\ 0& 0& \sin y\theta & \cos y\theta \end{array}\right)$$

$$f(q,x,y)=\left(\begin{array}{cccc}\cos x\theta & -\sin x\theta & 0& 0\\ \sin x\theta & \cos x\theta & 0& 0\\ 0& 0& \cos y\theta & -\sin y\theta \\ 0& 0& \sin y\theta & \cos y\theta \end{array}\right)\left(\begin{array}{c}{p}_1\\ p_2\\ p_3\\ p_4\end{array}\right)$$

基于Rope的长度外推能力（位置编码不同维度的频率角度）

## NTK
    def _dynamic_frequency_update(self, position_ids, device):
        """
        dynamic RoPE layers should recompute `inv_freq` in the following situations:
        1 - growing beyond the cached sequence length (allow scaling)
        2 - the current sequence length is in the original scale (avoid losing precision with small sequences)
        """
        seq_len = torch.max(position_ids) + 1
        if seq_len > self.max_seq_len_cached:  # growth
            inv_freq, self.attention_scaling = self.rope_init_fn(
                self.config, device, seq_len=seq_len, **self.rope_kwargs
            )
            self.register_buffer("inv_freq", inv_freq, persistent=False)  # TODO joao: may break with compilation
            self.max_seq_len_cached = seq_len

        if seq_len < self.original_max_seq_len and self.max_seq_len_cached > self.original_max_seq_len:  # reset
            self.register_buffer("inv_freq", self.original_inv_freq, persistent=False)
            self.max_seq_len_cached = self.original_max_seq_len
def _compute_dynamic_ntk_parameters(
    config: Optional[PretrainedConfig] = None,
    device: Optional["torch.device"] = None,
    seq_len: Optional[int] = None,
    **rope_kwargs,
) -> Tuple["torch.Tensor", float]:
#### 和标准Rope完全一致
    # seq_len: default to max_position_embeddings, e.g. at init time
    seq_len = seq_len if seq_len is not None and seq_len > max_position_embeddings else max_position_embeddings

    # Compute the inverse frequencies
    base = base * ((factor * seq_len / max_position_embeddings) - (factor - 1)) ** (dim / (dim - 2))
    inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2, dtype=torch.int64).float().to(device) / dim))
    return inv_freq, attention_factor


@torch.no_grad()
    def forward(self, x, position_ids):
        if "dynamic" in self.rope_type:
            self._dynamic_frequency_update(position_ids, device=x.device)

在应用NTK Rope时，每次对输入的x和position_ids，都会先在_dynamic_frequency_update函数看一下当前的长度是否超过了max_position_embeddings，如果超过则需要进行NTK内插，否则使用original_inv_freq，不做任何改变

在需要做内插的位置编码中，直接修改base，从而影响所有位置上的位置编码
base = base * ((factor * seq_len / max_position_embeddings) - (factor - 1)) ** (dim / (dim - 2))
当factor=1时，上式等于base*k

当$d/(d/2)$在d较高时接近1，则K可以看做外推的factor，但是实际应用起来基本外推4倍左右PPL就会上升了，这一点在YARN中得到了改进

YARN描述

NTK，YARN来自同样的作者团队，位置编码的内插方案作用在Embeding上而不是position上，这与之前的很多技术方案不一致；考虑到Rope的位置编码后对相对位置关系的建模
$$<f(q,m),f(k,n)>=Re[q{k}^{\ast }{e}^{i(m-n){\theta }_i}]$$
当m-n出现out of distribution的问题，模型可能会发生无法预测的行为造成效果下降，从极坐标旋转的角度看，$e^{i(m-n){\theta }_i}$表示将向量逆时针旋转$(m-n){\theta }_i$，从sincos位置编码画的图可以看出${\theta }_i=10000^{-2i/d}$是单调递减函数：相同的m-n设置下，位置编码的低维元素旋转速度快，高维元素旋转速度慢，即低维高频、高频低维

m-n的取值为$0-L_{train}$，可以认为低维元素是充分训练的，而高维元素没有充分训练，如何定量的标识“充分”程度呢？既然是旋转，则可以求解每个${\theta }_i$对应的周期，判断该元素是否在圆圈内充分训练：
$$T_i=\frac{2\pi }{{\theta }_i}$$
在$0-L_{train}$上，位置编码每个元素的最大旋转圈数为
$${\gamma }_i=\frac{L_{train}}{T_i}=\frac{L_{train}\ast {\theta }_i}{2\pi }$$
${\gamma }_i$就是m-n取最大值的时候，位置编码旋转的圈数，这个圈数必须>1，才说明该m-n距离是得到充分训练的，否则需要内插，压缩旋转角度到训练期间见过的长度范围，定义如下：
$$\begin{array}{c}{\theta }_i^{new}=\left[{\gamma }_i+(1-{\gamma }_i)\frac{L_{train}}{L_{test}}\right]{\theta }_i,{\gamma }_i=\{\begin{array}{rlr}& 1,& r_i>\tau \\ & 0,& r_i<1\\ & \frac{r_i-1}{\tau -1},& \text{others}\end{array}\end{array}$$