基于Matlab Function实现MPC横纵向耦合控制（快速实现硬件在环必备!!）

玉琯义

已于 2023-04-23 11:09:30 修改

阅读量1.8k

点赞数 9

CC 4.0 BY-SA版权

文章标签： matlab 开发语言

于 2023-04-23 10:06:16 首次发布

本文链接：https://blog.youkuaiyun.com/process98/article/details/130310755

文章介绍了使用模型预测控制(MPC)实现无人驾驶车辆的横向和纵向控制，通过MatlabFunction替代S-Function以适应特定硬件。代码示例展示了基于车辆动力学的状态量方程和控制量方程，以及如何将问题转化为二次规划进行求解，最终达到厘米级的路径控制精度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

MPC作为目前无人驾驶学术界广泛应用的算法，具有广阔的应用前景，利用MPC实现基于车辆动力学的横纵向控制已被百度Apollo开源放出（可见百度Apollo官网）。

但目前大多数使用Matlab进行仿真的MPC的模板都采用S-Function的形式来实现。而S-function在一些特定硬件在环设备上无法实现编辑，而Matlab Function可以完全兼容已有的设备。（我们实验室有的）。

下面放出代码，横向控制基于《Vehicle Dynamics and Control》，状态量分别为横向偏差、横向偏差率、航向偏差、航向偏差率(基于Frenet坐标系)。

kesi = [Lateral_error;Lateral_error_rate;Heading_error;Heading_error_rate]; %状态量6*1
%%状态量方程
A1 = [0,  1,  0,  0];%1*4
A2 = [0,  (C_af+C_ar)/(m*v_x),  -(C_af+C_ar)/m,  (a*C_af-b*C_ar)/(m*v_x)];
A3 = [0,  0,  0,  1];
A4 = [0,  (C_af*a-C_ar*b)/(I_z*v_x),  (C_ar*b-C_af*a)/I_z,  (C_af*a^2+C_ar*b^2)/(I_z*v_x)];

A = [A1;A2;A3;A4];%4*4
%%控制量方程
B = [0; -C_af/m; 0; -C_af*a/I_z];

%%扰动项方程
C1 = 0;
C2 = (C_af*a-C_ar*b)/(m*v_x)-dot_x;
C3 = 0;
C4 = (C_af*a^2+C_ar*b^2)/(I_z*(dot_x+0.001));

C = [C1;C2;C3;C4];%4*1
%%输出矩阵
F = [1,0,0,0];%1*4
%%离散化
A_k = ts*A + eye(4); %4*4
B_k = ts*B; %4*2
C_k = ts*C; %4*1

%%初始化矩阵
PHI = zeros(Np,4);
THETA = zeros(Np,Nc+1);
Omega = zeros(Nc+1,1);
ALUFA = zeros(Np,Nc+1);
 for j = 1:Np %行
        PHI(j,:) = F*A_k^j;
        for k = 1:Nc+1 %列
            if k <= j
                THETA(j,k) = F*A_k^(j-k)*B_k;
                ALUFA(j,k) = F*A_k^(j-k)*C_k;
            else
                 THETA(j,k) = 0;
                ALUFA(j,k) = 0;
            end
        end
 end

 for l = 1:Nc+1
     Omega(l,:) = phi_ades;
 end

%%转化为二次规划
%二次规划标准型
%min_x 1/2*x'*H*x + f'*x
error1 = PHI*kesi; %30*6*6*1=30*1
Qq = kron(eye(Np),Q); %30*30
Rr = kron(eye(Nc+1),R); %6*6
H = 2*THETA'*Qq*THETA + 2*Rr; %6*10*10*10*10*6 +6*6 = 6*6
g = (error1'-Y_desire'+Omega'*ALUFA')*Qq*THETA; % （1*10-1*10)*10*10*10*6=1*6
f = g'; %6*1
A_restrain = [];
b_restrain = [];
Aeq = [];
beq = [];
lb =[];
ub = [];
x0 = zeros(Nc+1,1);
options = optimoptions(@quadprog,'Display','iter','Algorithm','active-set');
X = quadprog(H,f,A_restrain,b_restrain,Aeq,beq,lb,ub,x0,options);


%%输出

delta_f = X(1);

纵向控制状态量为纵向偏差、纵向偏差率(基于Frenet坐标系)。

kesi = [Station_error;Speed_error]; %状态量2*1
%%状态量
A = [0,1;0,0];%2*2
%%控制量

B = [0;-1];

%%输出

F = [1,0];%1*2
%%离散化
A_k = ts*A + eye(2); %2*2
B_k = ts*B; %2*1


%%初始化矩阵
PHI = zeros(Np,2);
THETA = zeros(Np,Nc+1);

 for j = 1:Np %行
        PHI(j,:) = F*A_k^j;
        for k = 1:Nc+1 %列
            if k <= j
                THETA(j,k) = F*A_k^(j-k)*B_k;
            else
                THETA(j,k) = 0;
            end
        end
 end



%%转化为二次规划
%二次规划标准型
%min_x 1/2*x'*H*x + f'*x
error1 = PHI*kesi; 
Qq = kron(eye(Np),Q); 
Rr = kron(eye(Nc+1),R);
H = 2*THETA'*Qq*THETA + 2*Rr;
g = (error1'-Y_desire')*Qq*THETA; 
f = g'; 
A_restrain = [];
b_restrain = [];
Aeq = [];
beq = [];
%控制量为加速度与期望加速度的差值
lb =[];
ub = [];
x0 = zeros(Nc+1,1);
options = optimoptions(@quadprog,'Display','iter','Algorithm','active-set');
X = quadprog(H,f,A_restrain,b_restrain,Aeq,beq,lb,ub,x0,options);
%%输出
delta_acc = X(1);

imp_a = (delta_acc + a_p);

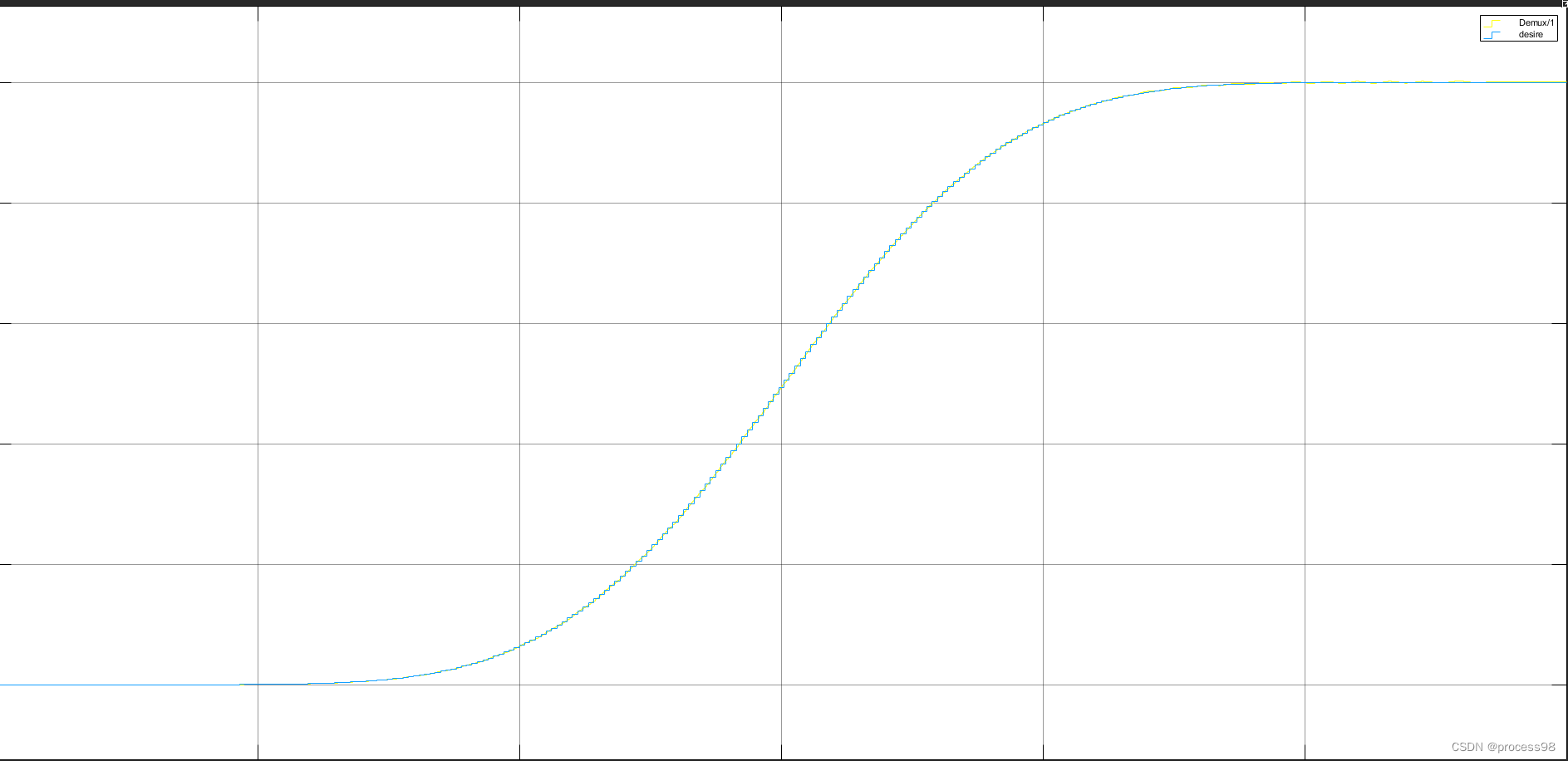
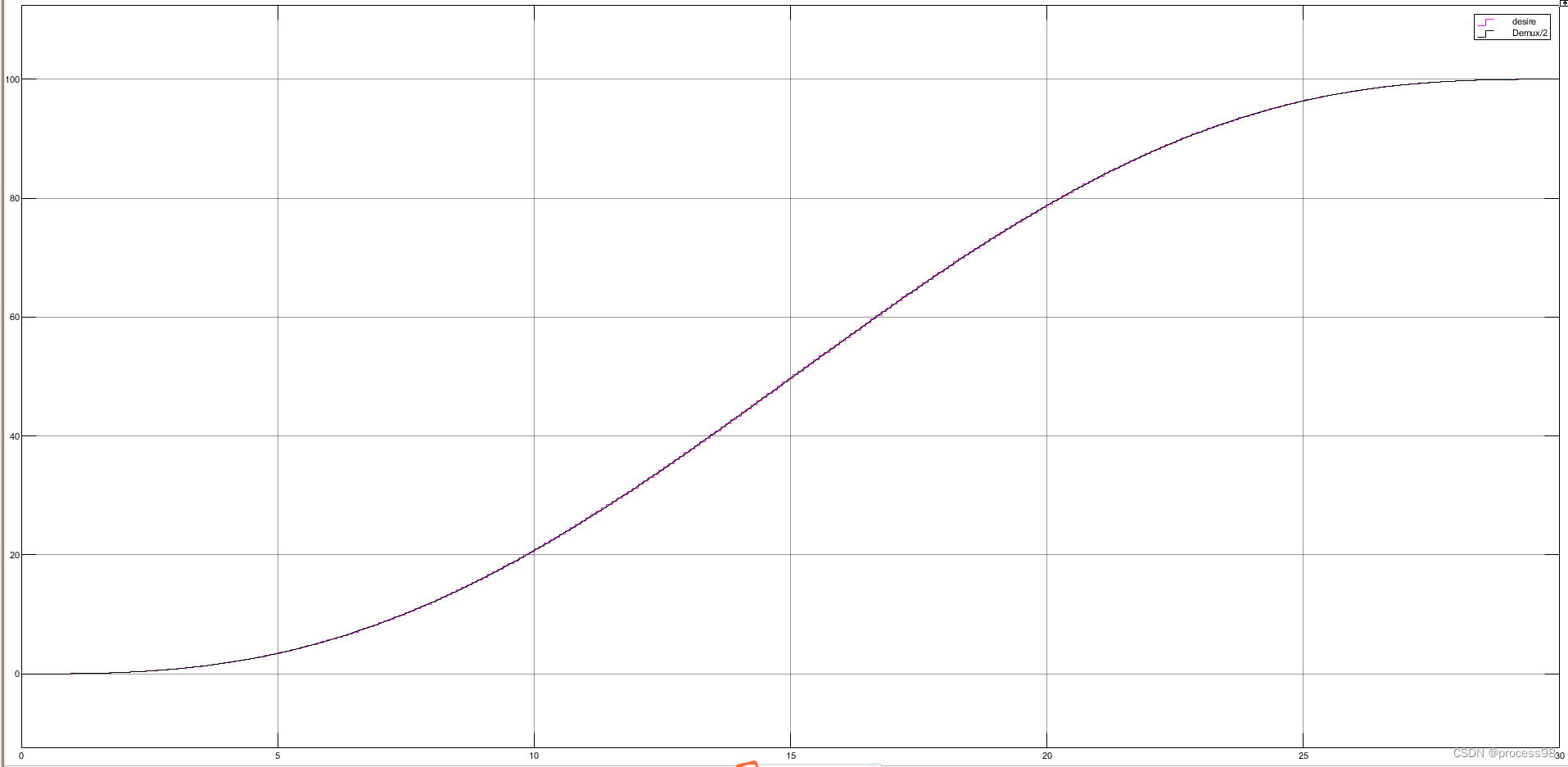
结果图：图1为横向期望路径与实际路径对比，图2为纵向期望路径与实际路径对比。

横纵向误差全部在厘米级的范围内，完全符合自动驾驶领域仿真的容许范围。