最近想用结构体来重新写一遍Dijkstra算法,结构体定义的变量使得对算法一些理解变得不那么抽象,在这里写下推导过程和代码。
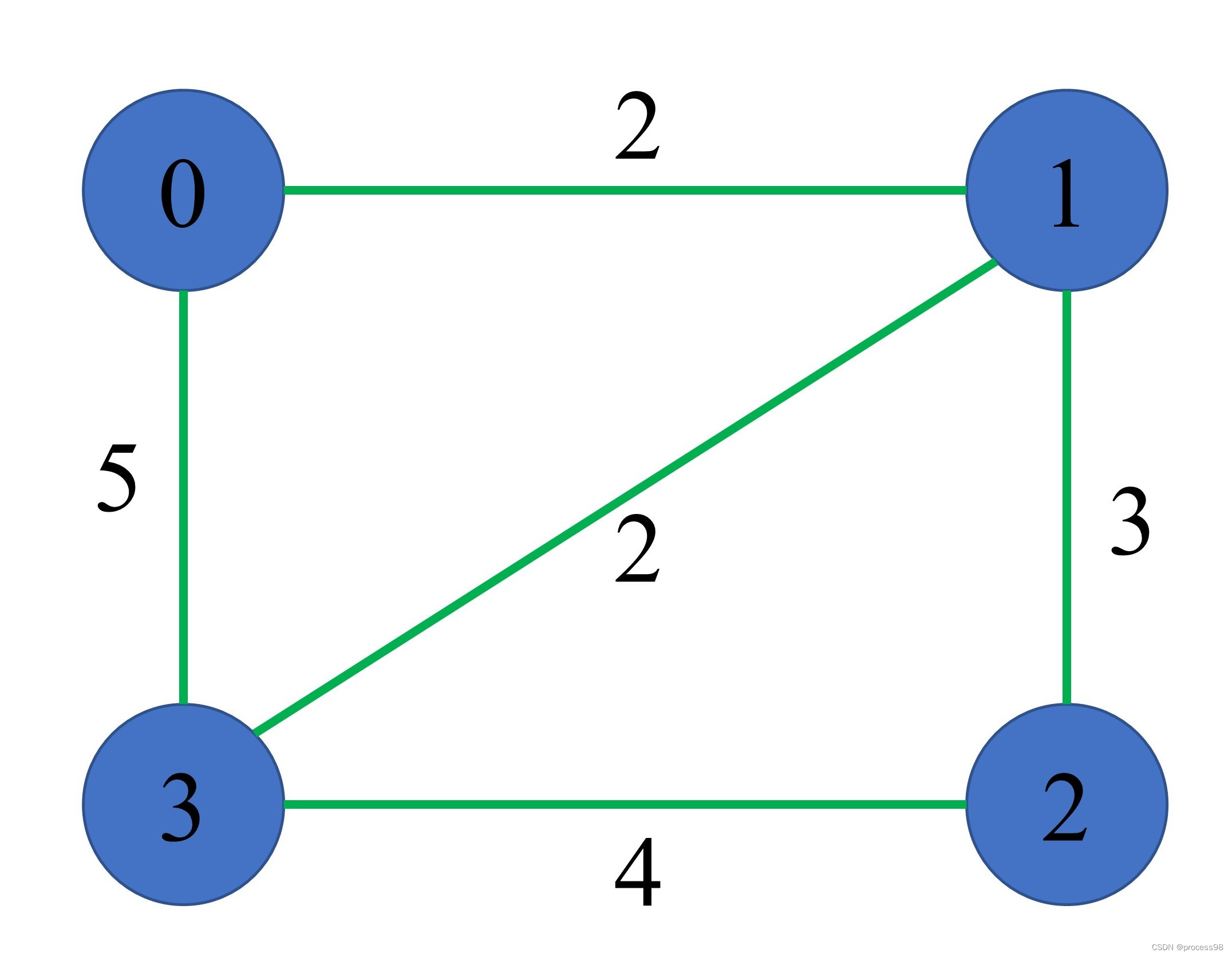
举例:蓝色圆圈代表节点,有四个节点:0、1、2、3。绿色边上的值代表经过这条边的代价系数。
目的:求出给定起始点和目标点的最小代价系数。
准备工作,定义一些需要的变量,分别为:无穷大、邻接矩阵(这里采用vector定义为动态数组,具体的大小根据输入而计算)、n和m代表顶点个数和边的个数、起始点和目标点、最后是一个结构体---DijkstraYGY_DiscretePoint,里面包括到起始点的距离(整数变量)和是否为最短距离(布尔值)。
#include <iostream>
#include <math.h>
#include <vector>
#include <limits>
const int inf_int = std::numeric_limits<int>::max();
std::vector<std::vector<int>> graph;
int n, m;
int start_point, destination_point;
struct DijkstraYGY_DiscretePoint
{
int Distance_from_start_point;
bool Whether_shortest_distance;
};
子函数一:生成邻接矩阵,函数输入:顶点个数和边个数
/*Subfunction, generate adjacency matrix*/
void generate_adjacency_matrix(int vertex_number, int edge_number)
{
graph.resize(vertex_number, std::vector<int>(vertex_number, inf_int));
int u, v, w;
for (int i = 0; i < vertex_number; i++)
{
graph[i][i] = 0;
}
for (int i = 0; i < edge_number; i++)
{
std::cout << "Please input the parameters required for the adjacency matrix" << std::endl;
std::cin >> u >> v >> w;
graph[u][v] = graph[v][u] = w;
}
std::cout << "Adjacency matrix generation completed." << std::endl;
std::cout << "The adjacency matrix is:" << std::endl;
for (int i = 0; i < vertex_number; i++)
{
for (int j = 0; j < vertex_number; j++)
{
std::cout << graph[i][j] << " ";
}
std::cout << std::endl;
}
}
子函数二:Dijkstra主体算法,这里最难理解的可能是第二个for循环的意义,当时也纠结好久。该循环的意义就在于寻找所有可能的中转点,试想如果没有该循环,函数计算一次最短距离就停止。也就是找到一个距离最短的中转点之后就再也不遍历,这样一来如果其他中转点如果由最优解就会被丢失。
void DijkstraYGY(int start, int destination, int vertex_number)
{
DijkstraYGY_DiscretePoint_Vector.resize(vertex_number);
for (int i = 0; i < vertex_number; i++)
{
DijkstraYGY_DiscretePoint_Vector[i].Distance_from_start_point = graph[start][i];
DijkstraYGY_DiscretePoint_Vector[i].Whether_shortest_distance = false;
}
DijkstraYGY_DiscretePoint_Vector[start].Whether_shortest_distance = true; /*Starting point joining a known set*/
int Minimum_distance, Minimum_distance_point;
Minimum_distance = inf_int;
for (int i = 0; i < vertex_number; i++)/*The significance of variable i lies in finding all the transition points*/
{
for (int j = 0; j < vertex_number; j++)
{
if (DijkstraYGY_DiscretePoint_Vector[j].Whether_shortest_distance == false && DijkstraYGY_DiscretePoint_Vector[j].Distance_from_start_point < Minimum_distance)
{
Minimum_distance = DijkstraYGY_DiscretePoint_Vector[j].Distance_from_start_point;
Minimum_distance_point = j;
}
}
DijkstraYGY_DiscretePoint_Vector[Minimum_distance_point].Whether_shortest_distance = true; /*Transition point joining a known set*/
for (int j = 0; j < vertex_number; j++)
{
if (DijkstraYGY_DiscretePoint_Vector[j].Whether_shortest_distance == false && DijkstraYGY_DiscretePoint_Vector[j].Distance_from_start_point > DijkstraYGY_DiscretePoint_Vector[Minimum_distance_point].Distance_from_start_point + graph[Minimum_distance_point][j])
{
DijkstraYGY_DiscretePoint_Vector[j].Distance_from_start_point = DijkstraYGY_DiscretePoint_Vector[Minimum_distance_point].Distance_from_start_point + graph[Minimum_distance_point][j];
}
}
}
std::cout << "The shortest distance from the starting point to the destination point is:" << DijkstraYGY_DiscretePoint_Vector[destination].Distance_from_start_point << std::endl;
}
函数主体
/*Main Function*/
int main()
{
std::cout << "Please input the number of vertex and edge:" << std::endl;
while (std::cin >> n >> m)
{
generate_adjacency_matrix(n, m);
std::cout << "The adjacency matrix is:" << std::endl;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
std::cout << graph[i][j] << " ";
}
std::cout << std::endl;
}
std::cout << "Please the start and destination points:" << std::endl;
std::cin >> start_point >> destination_point;
DijkstraYGY(start_point, destination_point, n);
}
return 0;
}
运行测试:
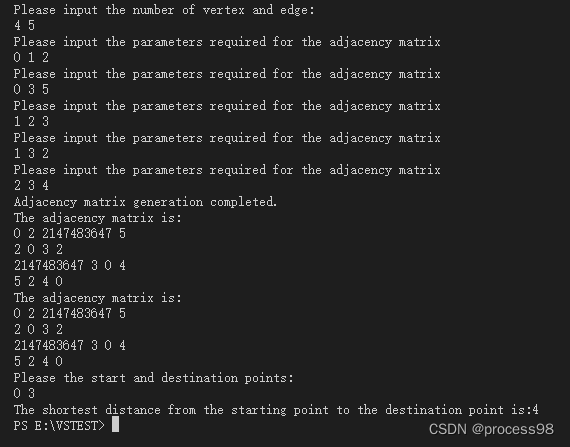




 本文详细描述了如何使用结构体重写Dijkstra算法,包括定义变量、邻接矩阵的生成、算法主体,以及如何处理起始点和目标点,以求解两点之间的最小代价路径。
本文详细描述了如何使用结构体重写Dijkstra算法,包括定义变量、邻接矩阵的生成、算法主体,以及如何处理起始点和目标点,以求解两点之间的最小代价路径。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








