频谱混叠
“时域的相乘等于频域的卷积,时域的卷积等于频域相乘”
对于一个连续的信号采样,采样后的频谱相当于将采样前的频谱进行延拓,延拓的周期就是采样率。
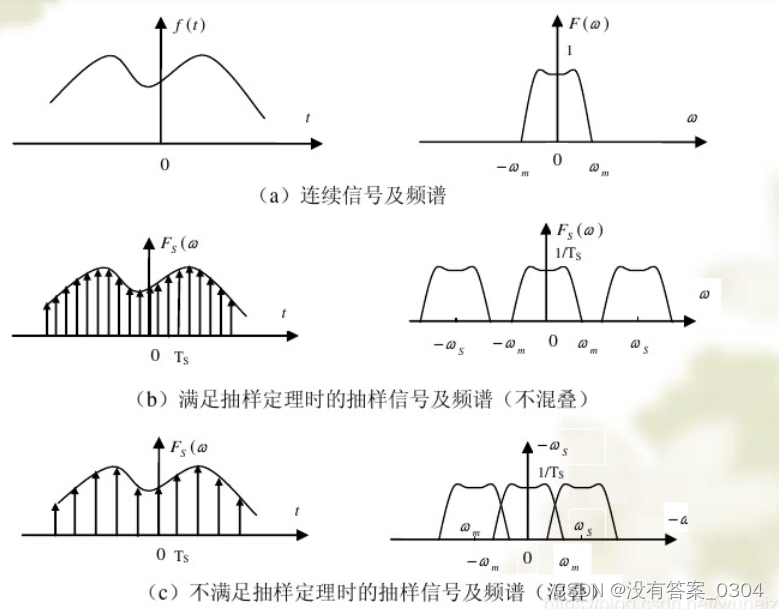
频谱混叠和奈奎斯特采样
最新推荐文章于 2025-12-03 10:01:15 发布
频谱混叠
“时域的相乘等于频域的卷积,时域的卷积等于频域相乘”
对于一个连续的信号采样,采样后的频谱相当于将采样前的频谱进行延拓,延拓的周期就是采样率。

 2937
2937

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


