RNN及变体LSTM、GRU（在NILM中的应用）_bi-directional gru-优快云博客

本文链接：https://blog.youkuaiyun.com/phoenixlxl/article/details/129326942

本文介绍了RNN的结构和参数共享机制，以及梯度消失和梯度爆炸问题。为了解决这些问题，文章详细阐述了LSTM的长短期记忆机制和三扇门（输入门、遗忘门、输出门）的工作原理，以及GRU如何通过更新门和重置门简化LSTM的复杂性，同时保持良好的性能。LSTM和GRU都是为了解决RNN的长期依赖问题而提出的变体，各有优缺点，适用于不同的应用场景。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

RNN(Recurrent Neural Network)循环神经网络

1、介绍

卷积神经网络等的输入和输出都是相互独立的，而RNN拥有记忆能力，其记忆能力依赖于输入和输出

网络结构如下图所示：

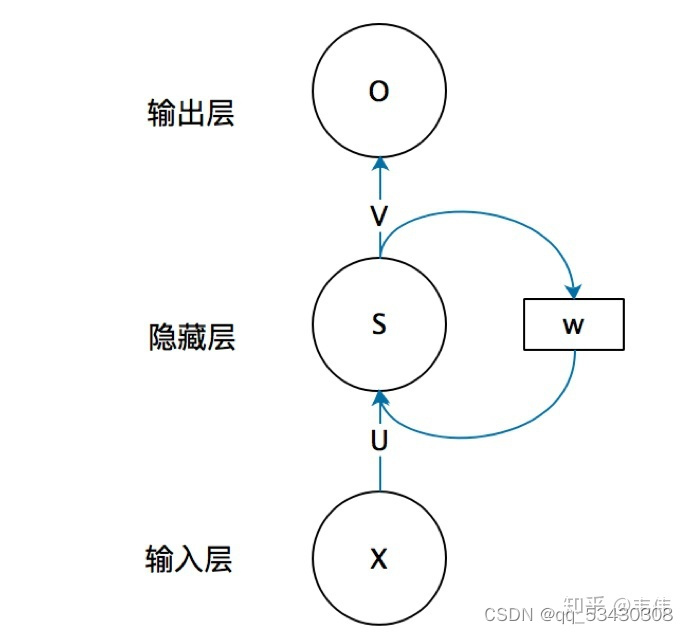
展开结构如下：

参数共享:

Wo 、Ws 、Wx 为参数，通过梯度下降不断更新，三个参数在一个神经单元(cell)中是共享的

在 t 时刻：

输入为

$X_{t}$

该时刻记忆：

$S_{t}=f(W_{X}*X_{t}+S_{t-1}*W_{S})$

输出为：

即：t时刻的输出不仅与当前时刻的输入有关，还与前一时刻的记忆有关

2、存在的问题——梯度消失和梯度爆炸

对t3时刻的代价函数求偏导：

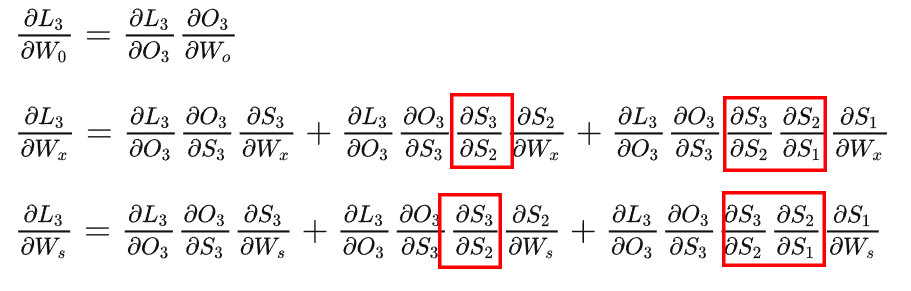
通过上式可推导出任意时刻对Wx、Ws求偏导的一般公式：

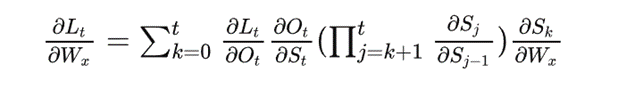
Ws同理。

又因为：

所以：

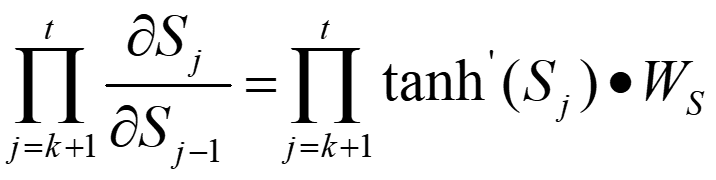
即在反向传播过程中对Wx和Ws求偏导时会乘以tanh函数的导数，网络层数越深乘上的导数越多。这是因为St随着时间序列向前传播，而St又是Ws、Wx的函数

又因为如下图所示tanh函数的导数不大于1

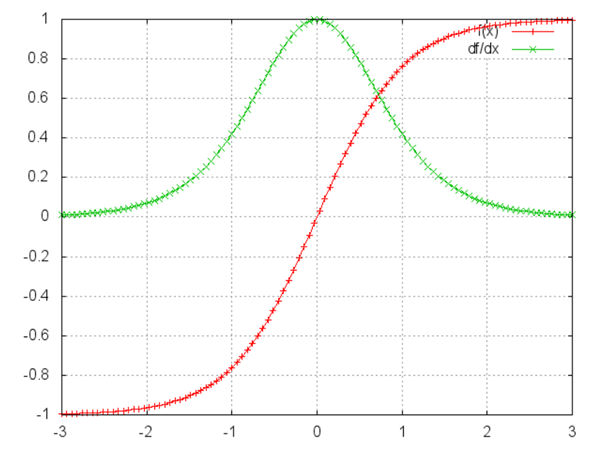
因此当Ws也是一个大于0但是小于1的数时，越深的层中较远的层的信息就会越趋近于0，即梯度消失

当Ws是一个足够大的数时，越深的层中较远的层的信息就会越趋近于正无穷，即梯度爆炸

（RNN中的梯度消失不是指损失对参数的总梯度消失了，而是RNN中对较远时间步的梯度消失了）

在神经网络中使用较小梯度进行更新的层会停止学习，导致RNN会忘记过早的内容，因此称其为具有短时记忆的神经网络

解决方案：RNN的变体LSTM、GRU

变体一：Long Short-Term Memory (LSTM)长短期记忆网络

相比于原始的RNN的隐层(hidden state)， LSTM增加了一个细胞状态Ct(cell state)

下图表示 t 时刻的输入输出：

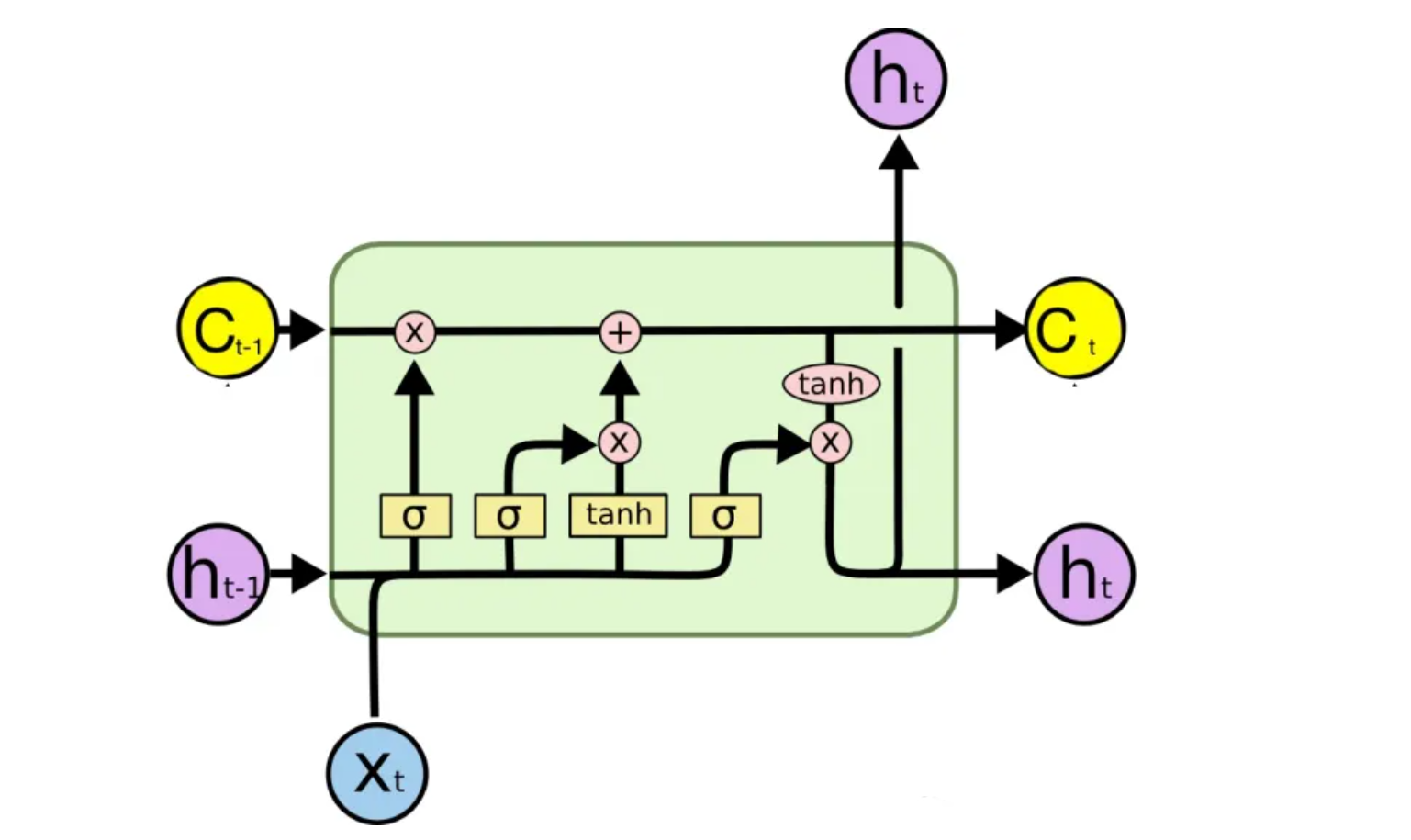
解释：

神经网络（黄色方框）：

表示一层神经网络，也就是w^T x + b的操作。区别在于使用的激活函数不同，σ表示的是softmax函数，他是将数据压缩到[0，1]范围内，如下图所示；tanh表示的是双曲正切激活函数，他把数据归一化到[-1，1]之间

细胞状态Ct（黄色圆圈）：

t-1 时刻的细胞状态Ct-1，通过上一时刻的隐层状态ht-1与当前时刻的输入Xt进行适当的修改（具体操作为通过遗忘门与输入门进行计算，见下文）得到当前时刻的细胞状态Ct，如下图所示：

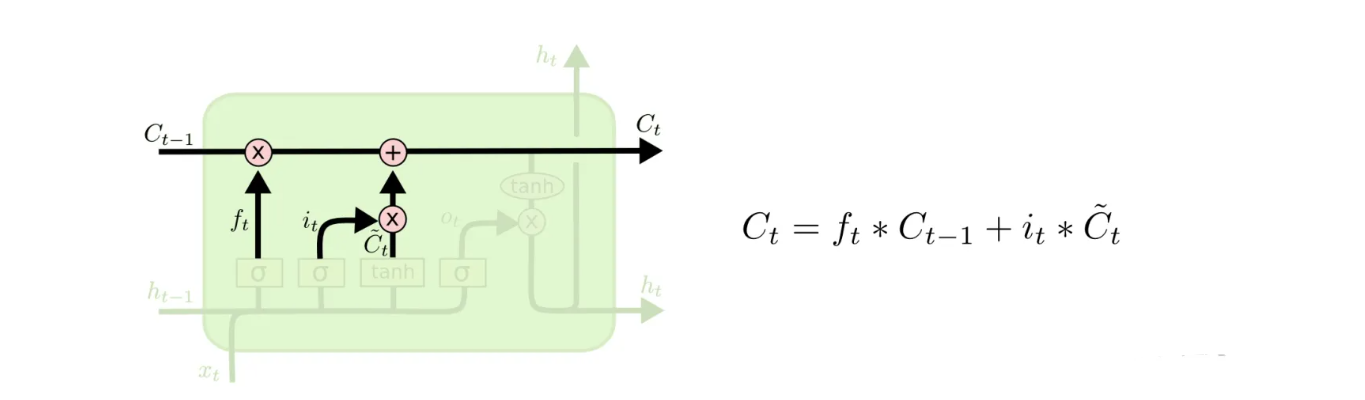
此外，Ct会参与当前时刻的隐层输出ht的计算

隐层状态ht（紫色圆圈）：

t -1 时刻的隐层状态ht-1，通过“门”对细胞状态Ct进行修改，并参与计算当前时刻的细胞状态Ct

ht不仅是由上一个状态，和本次的输入所决定，还有一个细胞状态Ct-1，这是其与RNN最大的不同

LSTM的三扇门（均包含sigmoid函数）：

输入门：

选择保留部分当前输入的信息，输入前一层的信息，接近1的信息表示更为重要

其次还要将前一层隐藏状态的信息和当前输入的信息传递到 tanh 函数中去，创造一个新的侯选值向量。最后将 sigmoid 的输出值与 tanh 的输出值相乘，sigmoid 的输出值 it 将决定 tanh 的输出值中哪些信息是重要且需要保留下来的

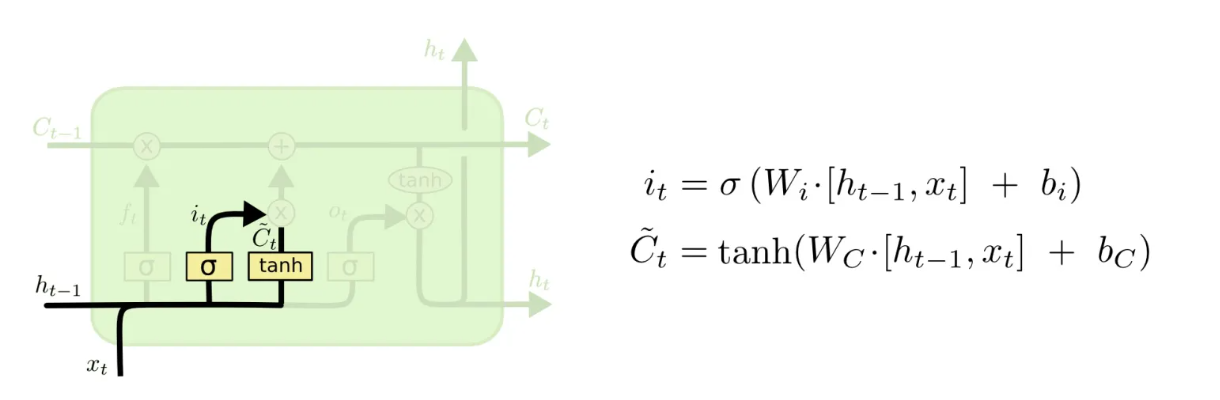
遗忘门：

选择丢弃哪些细节

越靠近1的信息越可能被保存，越接近0的信息越可能被遗忘。下图中遗忘门的输出ft与上一时刻的细胞状态Ct相乘即可选择遗忘哪些细节。

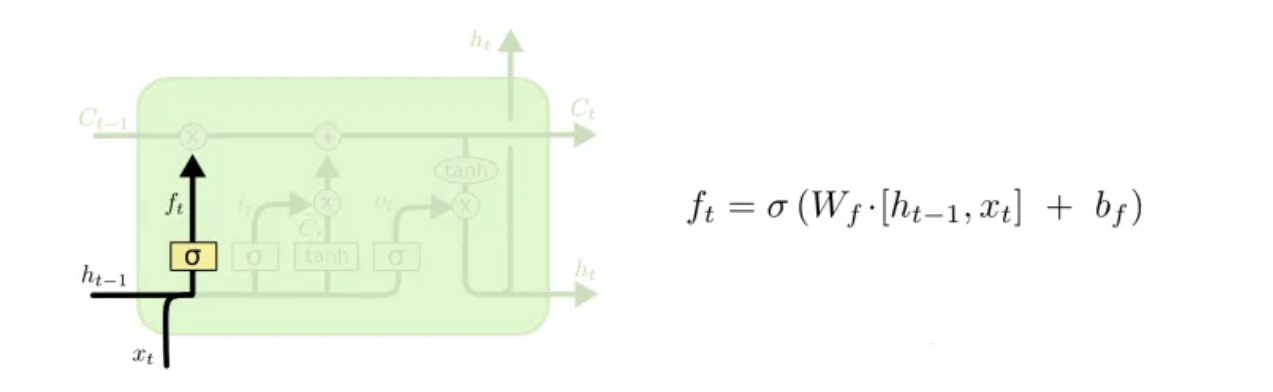
输出门：

通过输入以及记忆块决定输出

”门“的存在使得LSTM能够让有用的信息在记忆中长期保存，理论上能一直保存

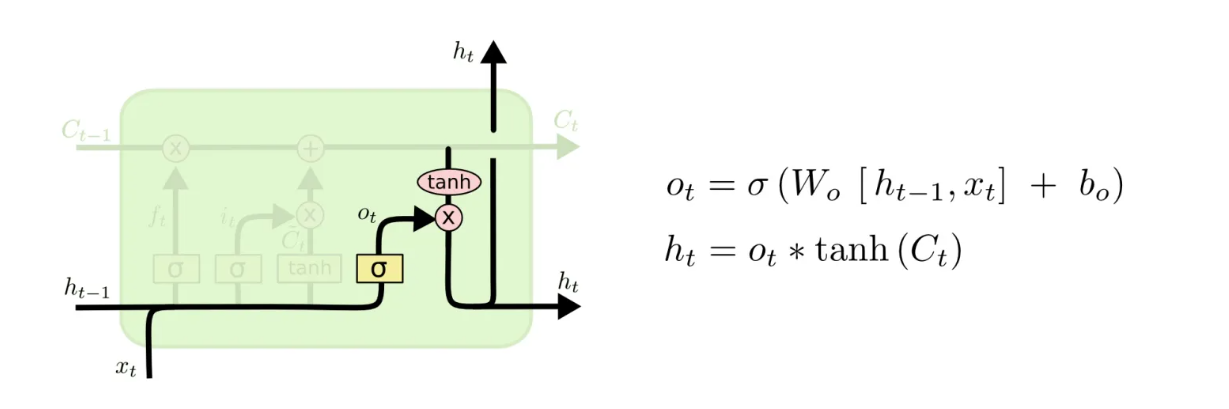
LSTM为什么能够解决梯度消失和梯度爆炸：

通过训练让“门”学习保存哪些信息，丢弃哪些信息。

LSTM的变式：带窥孔的LSTM：

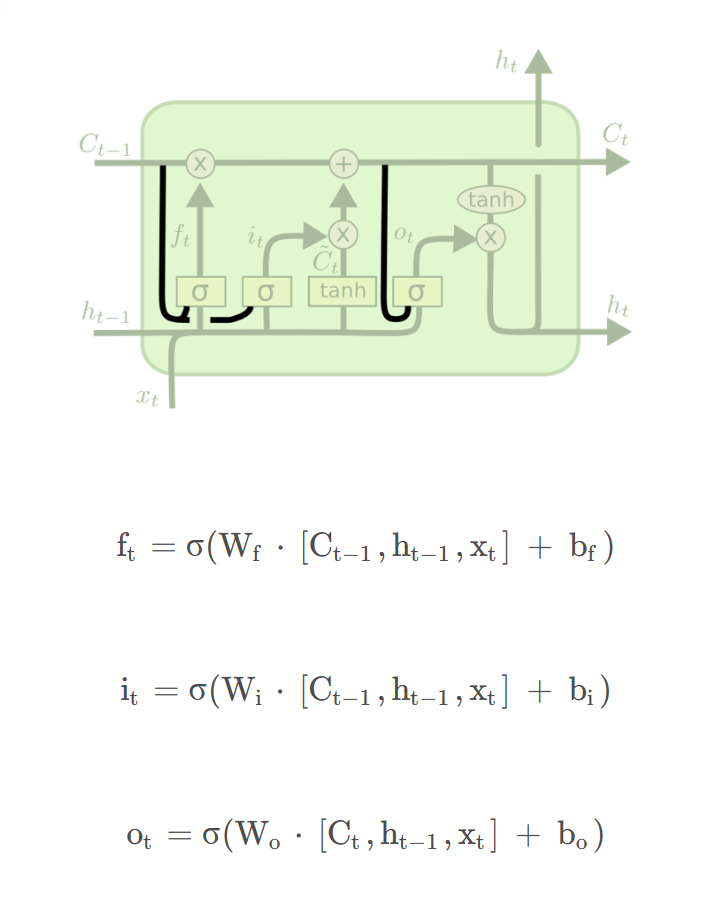
弥补网络的一个缺点：当前的细胞状态不能影响到三个门在下一时刻的输出，使整个细胞状态对上一单元模块的序列处理中丢失了部分信息，因此在内部网络结构中加入了窥孔连接，该连接可以让门观察到细胞状态。具体网络结构如下

构建LSTM（用于NILM）:

1. Input (length determined by appliance duration)

2. 1D conv (filter size=4, stride=1, number of filters=16, activation function=linear, border mode=same)

3. Bidirectional LSTM (N=128, with peepholes)

4. Bidirectional LSTM (N=256, with peepholes)

5. Fully connected (N=128, activation function=TanH)

Python实现：

        # Creates the RNN module described in the paper
        model = Sequential()            #顺序模型，即通过一层层神经网络连接构建深度神经网络
        # 1D Conv   一维卷积层
        model.add(Conv1D(16, 4, activation="linear", input_shape=(time_stamp,1), padding="same", strides=1))
        #Bi-directional LSTMs
        model.add(Bidirectional(LSTM(128, return_sequences=True, stateful=False), merge_mode='concat'))
        model.add(Bidirectional(LSTM(256, return_sequences=False, stateful=False), merge_mode='concat'))
        # Fully Connected Layers
        model.add(Dense(128, activation='tanh'))
        model.add(Dense(1, activation='linear'))
        model.compile(loss='mse', optimizer="adam")

变体二：Gate Recurrent Unit(GRU)门控循环单元

介绍：

GRU为新一代的循环神经网络，与LSTM类似

但是去掉了细胞状态Ct，使用隐藏状态来进行信息的传递，只包含更新门和重置门

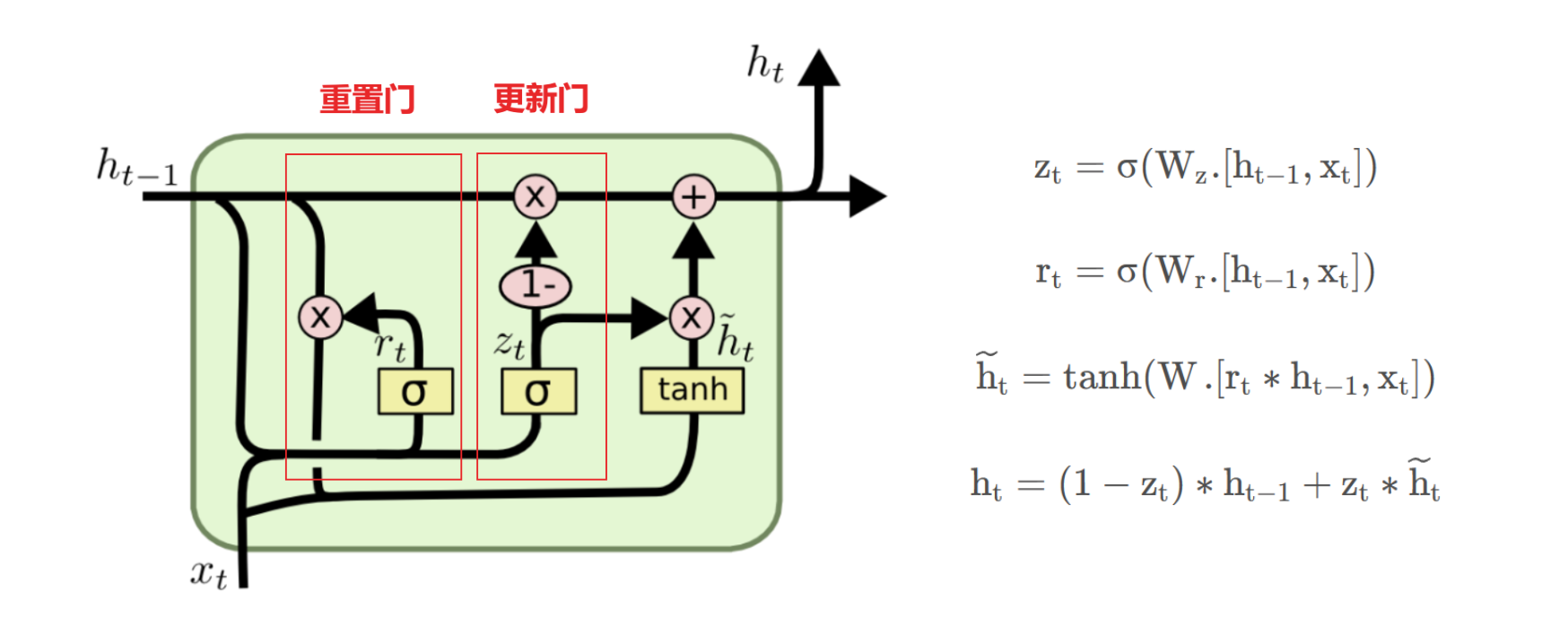
更新门：

GRU将LSTM中的输入门与遗忘门合二为一，称为更新门，用于控制前一时刻传递来的信息有多少能够被继续保留

重置门：

选择一定的信息丢弃（遗忘）

GRU的优势：

GRU的参数量少，减少过拟合的风险

LSTM的参数量是Navie RNN的4倍，参数量过多就会存在过拟合的风险，GRU只使用两个门控开关，达到了和LSTM接近的结果。其参数量是Navie RNN的三倍

GRU的构建：

1. Input (length determined by appliance duration)

2. 1D conv (filter size=4, stride=1, number of filters=16, activation function=ReLU, border mode=same)

3. Bidirectional GRU (N=64, activation function=ReLU)

4. Bidirectional GRU (N=128, activation function=ReLU)

5. Fully connected (N=128, activation function=ReLU)

6. Output: Output: Number of units:1, activation: linear

Python实现：

        model = Sequential()

        # 1D Conv
        model.add(Conv1D(16, 4, activation="relu", padding="same", strides=1, input_shape=(time_stamp,1)))
        #Bi-directional GRUs
        model.add(Bidirectional(GRU(64, activation='relu', return_sequences=True), merge_mode='concat'))
        model.add(Dropout(0.5))
        model.add(Bidirectional(GRU(128, activation='relu', return_sequences=False), merge_mode='concat'))
        model.add(Dropout(0.5))

        # Fully Connected Layers
        model.add(Dense(128, activation='relu'))
        model.add(Dropout(0.5))
        model.add(Dense(1, activation='linear'))
        model.compile(loss='mse', optimizer="adam")