例题11

例题12

1、知识点总结

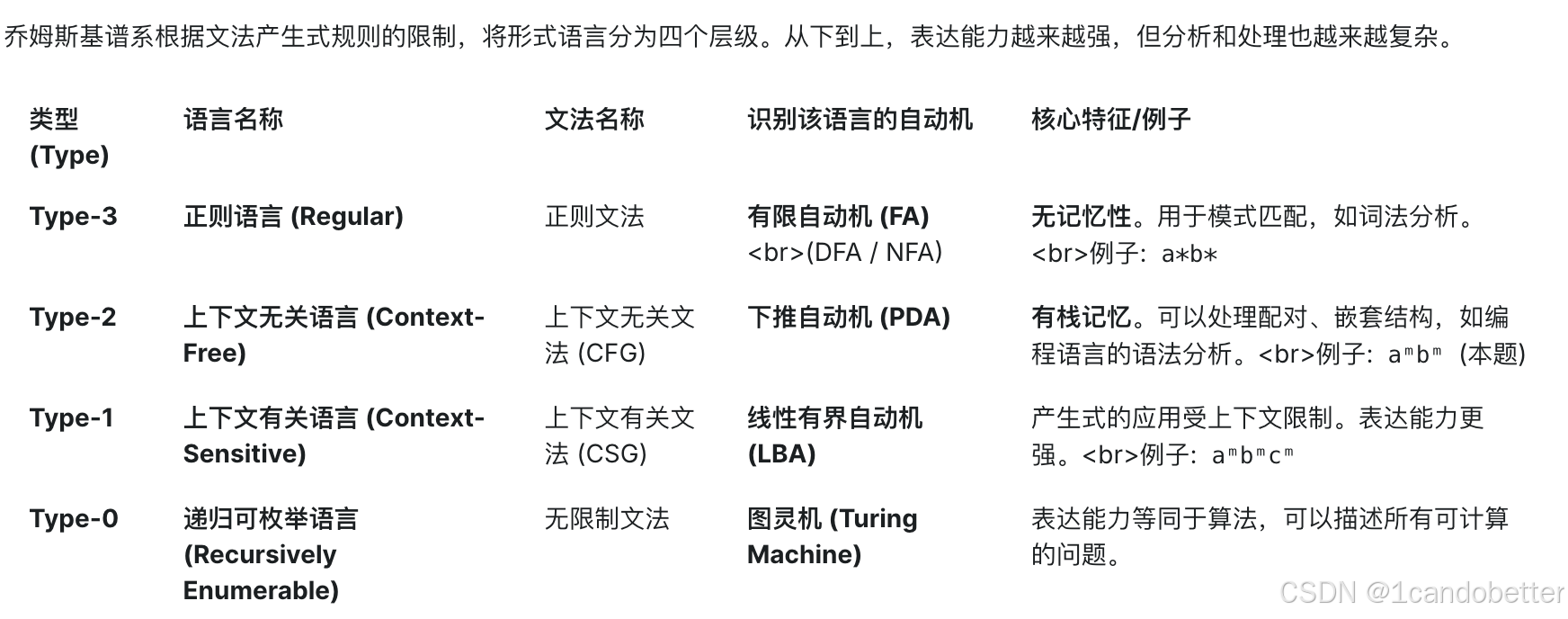
2、选项分析
A. 可用正则式 a*b* 表示
-
这个说法是错误的。 正则表达式 a*b* 表示“零个或多个 a”后面跟着“零个或多个 b”。它能匹配 aaabb,ab,aaabbbb 等 a 和 b 的数量不相等的字符串。而语言 L 严格要求 a 和 b 的数量必须相等。因此,a*b* 描述的语言集合远大于 L
B. 不能用正则式表示,但可用不确定的有限自动机识别
-
这个说法是错误的。 根据克莱尼定理 (Kleene's Theorem),正则表达式、确定的有限自动机 (DFA) 和不确定的有限自动机 (NFA) 在表达能力上是完全等价的。如果一个语言不能用正则表达式表示,那么它也绝对不能被任何有限自动机(无论是DFA还是NFA)所识别。
C. 可用正则式 aᵐbᵐ 表示
-
这个说法是错误的。 aᵐbᵐ 不是一个标准的正则表达式。正则表达式的语法中不包含这种用来表示“计数和回溯引用”的变量 m。标准的正则表达式只能表达有限次的重复(如 a{5})或者不确定但无关联的重复(如 a*)。它无法表达“b 的数量必须等于前面 a 的数量”这种依赖关系。
D. 不能用正则式表示,但可用上下文无关文法表示
-
这个说法是正确的。
-
为什么不能用正则式表示? 正则表达式的计算模型是有限自动机。有限自动机的核心特征是它只有有限的内存(即它的状态)。要识别 aᵐbᵐ,自动机必须在读取 a 的时候“记住” a 的数量,然后在读取 b 的时候进行“核对销账”。如果 m 可以是任意大的数字,那么有限个状态是绝对无法记住任意数量的 a 的。这就是正则语言的泵引理 所要证明的核心。
-
为什么可用上下文无关文法表示? 上下文无关文法 (Context-Free Grammar, CFG) 的计算模型是下推自动机,它比有限自动机多了一个无限容量的栈 (Stack)。这个栈完美地解决了“计数”问题。我们可以用一个简单的上下文无关文法来定义语言
3、最终答案:D
例题13

1、知识点总结
这道题考察的是上下文无关文法 (Context-Free Grammar, CFG) 所定义的语言 (Language) 的精确概念。
根据形式语言的标准定义,一个文法 G 所产生的语言 L(G) 是指:从开始符号 S 出发,经过零次或多次产生式的推导,所能得到的所有完全由终结符组成的字符串的集合。

2、选项分析
A. 从 S 出发推导出的包含 V 和 T 中所有符号的串
-
这个说法
 程序语言处理习题解析
程序语言处理习题解析





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 840
840

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








