低功率DBD中PFM调制分析

低功率应用中脉冲频率调制介质阻挡放电的分析与设计

1 引言

介质阻挡放电（DBD）已广泛应用于材料处理、臭氧生成、生物医学等领域。放电过程中产生的等离子体或臭氧可用于材料表面特性改性、灭菌和化学气相沉积（Fang et al., 2006；Wang 和 He，2006；Burany et al., 2008；Wedaa et al., 2011；Kostov et al., 2013）。通常，如图1a所示，将交流高压施加到负载上，以在工业应用中产生放电，因为这样便于功率调节。方法简单、拓扑结构简洁且可靠性高。当外加电压足够高时，电介质与高压电极之间的空气发生击穿，从而引发电晕放电。由于电晕放电发生时气隙两端的电压几乎保持恒定（Alonso et al., 2003），DBD负载的等效电路如图1a所示，其中C g_s表示气隙的等效电容，Cd s 表示电介质的等效电容（Wagner et al., 2003；Williamson et al., 2006；Bonaldo 和 Pomilio，2010）。二极管桥电路用于模拟恒定电晕放电电压的双向电压钳位特性。为了产生所需的交流高压，通常采用谐振变换器以及高频高变比变压器，以实现电气隔离。

在高功率介质阻挡放电应用中，变压器的寄生电容远小于DBD负载的等效电容因而可忽略不计。因此，采用电感‐电容‐电容（LCC）串并联谐振变换器作为等效电路，该电路已在许多论文中讨论过（Gilbert et al., 2007；Fu et al., 2008；Martin‐Ramos et al., 2008）。然而，在低功率应用中，如小尺寸材料处理或便携式医疗设备，DBD负载的等效电容与变压器的寄生电容处于同一数量级。因此，必须考虑寄生电容的影响，传统LCC谐振变换器不再适用于分析，需进一步讨论寄生电容的影响。此外，为了提高便携性和降低成本，通过应用磁集成技术将谐振电感集成到变压器中（Fu et al., 2008），因此仅需一个磁性元件（图1b）。

本文所用符号见表1。

为简化分析，基于基波近似（FHA）方法，采用与阻性元件并联的电容（RC）作为DBD负载的等效电路（Alonso et al., 2003；金纳雷斯和霍通坎，2010）。然而，由于存在二极管桥电路，FHA在稳态分析中精度不足。因此，采用整流补偿基波近似（RCFHA）（Shafiei et al.，2013）用于带整流桥的谐振变换器的稳态分析。

表1 本文使用的符号

参数	含义
Cd	折算到变压器初级侧的介质等效电容
Cg	折算到变压器初级侧的气隙等效电容
VT	折算到变压器初级侧的放电维持电压
Ls	变压器漏感
Cp	折算到变压器的寄生电容
n	变压器匝数比
f s	工作频率
ωs	工作角频率，ωs=2πf s
f 0	谐振频率
Vin	逆变器的母线电压
vab	逆变器输出电压
vae	电极施加电压
Vae	vae 的峰值
Gr	谐振槽路增益，Gr=Vae/(nVin)
vcd	施加到 Cd 的电压
icd	流经Cd的电流
vcg	施加到Cg的电压
ir	变压器初级侧的谐振电流
Ir	i 的峰值数值 r
Pin	平均输入功率
Pout	平均输出功率
ks	负载等效电容比，ks=Cd/Cg
k p	kp =Cp/Cd
ψ	充电角度 Cg
φ	输出电压之间的相位误差 逆变器和谐振电流
tdb	死区时间
td	驱动信号上升沿之间的时间延迟 信号及其对应的过零点 谐振电流的点
t p e	上升沿与全之间的时延 桥式输出电压和谐振 电流
X y _norm	归一化变量 Xy
X y _s	变量 Xy 折算到变压器的 次级侧
X y 1	Xy的基波分量
X y A	傅里叶正弦项系数 X y 1 在f s
X y B	傅里叶余弦项系数 X y 1 在f s

2 变换器分析

2.1 稳态分析

一个与电阻串联的电容器用于对RCFHA中的 Cg和整流器进行建模。因此，该分析比FHA中使用电阻等效的方法更加准确。为了简化分析，所有参数均折算到变压器的初级侧（图2a）。

谐振变换器的关键波形如图2b所示。由于折算到变压器原边的谐振电流r(t)几乎为正弦的，因此假设其等于基波分量。即，

$$ r1 r r s () () sin( ). i t i t I \omega t = = (1) $$

根据Cg是否被钳位，电路工作可分为四个阶段。在前半个周期中，当ir(t)从零开始增加时，Cg由−VT充电，其等效电路如图3a所示。因此，可得到以下方程：

$$ cd r s p p s 1 () sin( ), 1 i t I t k k k \omega = + + (2) $$

$$ r cg T s s g p p s () (1 cos( )). (1 ) I v t V t C k k k \omega \omega = - + - + + (3) $$

在此阶段结束时，vcg(t) 增加到 VT。也就是说，

$$ cg T s . v V \psi \omega \left( \right) = \left( \right) (4) $$

将式(4)代入式(3)，可推导出以下方程：

$$ T s g p p s r 2 (1 ) cos 1 . V C k k k I \omega \psi + + = - (5) $$

然后Cg充电至VT ，并保持钳位直到ir(t)振荡到零。因此，等效电路变为图3b所示的电路。在此阶段，icd(t)和vcg(t)由以下公式给出

$$ cd r s p 1 () sin( ), 1 i t I t k \omega = + (6) $$

$$ c g T () . v t =V (7) $$

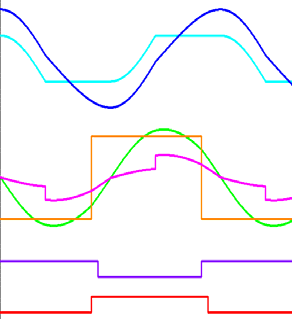和关键波形(b))

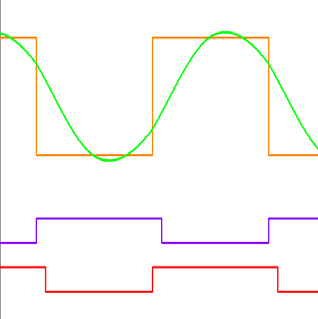和被钳位(b)时的等效电路)

2.2 性能分析

PFM通常用于调节输出功率，因其控制策略简单且能实现零电压开关（ZVS）（刘和何，2005）。随着工作频率的增加，输出功率降低，并在整个功率范围内实现零电压开关。对于从轻载到满载的谐振变换器，期望其工作频率范围较窄，因为变压器的击穿电压随频率增加而显著下降（Shafiei et al., 2011）。

另一方面，峰值施加电极电压在微放电数量和表面处理效果中起着重要作用（吉巴洛夫和皮茨，2000；Jidenko et al., 2006），其随输出功率而变化。在材料处理过程中，过高的施加电极电压可能会损坏甚至烧毁材料，而过低的电压则可能导致放电不稳定并造成处理不均匀。因此，有必要研究Cp对fs和Vae的影响。

当谐振槽路工作在谐振状态时，其呈阻性，因此谐振频率可由公式(20)推导得出。图5展示了不同Cp下的谐振工作频率和槽路增益。谐振频率随Cp的减小而增加，从而实现高功率密度。然而，在需要恒定Vae以维持稳定放电的情况下，谐振变换器的槽路增益同时会降低，且开关的电压应力增大。因此，必要时需进行权衡。

为了简化PFM中的分析，采用了归一化结果（Gilbert et al., 2007）。图6a示出了从满载到轻载时具有不同Cp的谐振变换器的归一化频率，其中Cp=0表示该变换器为无寄生电容的传统LCC谐振变换器。图6b显示了归一化的峰值施加电极电压。此外，DBD负载的等效电容随峰值施加电极电压而变化。Cd随着Vae的减小从48 nF降至32 nF，而Cg被假定为恒定的16 nF，这与Wang et al. (2005)的结论一致。图6a中的曲线表明，较大的Cp会导致从满载到轻载的频率范围更窄，因为Cp抵消了DBD负载非恒定等效电容的影响，从而简化了变压器设计并提高了可靠性。

另一方面，在PFM中，较大的Cae会使 ae下降得更快，这可能影响放电稳定性并改变特性。因此，在根据要求选择Cp时应进行折衷考虑。

3 设计考虑

基于第2节中推导出的表达式，以指定的DBD负载为例介绍了设计流程。该DBD负载由两个圆形平面电极和一块厚度为1 mm的平板石英电介质组成，如图1a所示。高压电极、石英电介质和接地电极的直径分别为3 cm、5 cm和6 cm。额定条件下负载的参数列于表2中。在带有DBD负载的谐振变换器中，工作频率是一个略高于实现零电压开关的谐振频率，如图7所示。当开关S1和S4导通时，谐振电流流过反并联二极管，两个开关两端的电压为零。因此实现了零电压开关，td定义为驱动信号上升沿与对应电流过零点之间的时间延迟。通过将死区tdb加到td上，得到逆变器输出电压超前于谐振电流的总时间tpe。在本研究中，在额定条件下，tdb和tpe分别设定为2 μ秒和4 μ秒。

由于应用了磁集成技术，只需确定三个参数：n、Ls 和 Cp。对于明确的 n 和 Cp，可通过结合公式(5)和(8)推导出Ir和ψ：

$$ in p r T s g p p s T π(1 ) (1 ), 2 P k I V C k k k V \omega + = + + + (24) $$

$$ 2 in p T s g p p s 2 in p T s g p p s π(1 ) 2 (1 ) arccos . π(1 ) 2 (1 ) P k V C k k k P k V C k k k \omega \psi \omega \left( \right) + - + + = \left( \right) \left( \right) + + + + (25) $$

因此，得到Req、Xeq和Rin，分别对应公式(16)、(17)和(19)。然后可通过将公式(19)、(20)和(24)代入公式(22)推导出Ls：

$$ 2 2 ab in s s r s 2 2 2 p e p s e eq 2 2 4 2 2 2 s p e s p e eq 4 π . ( ) V R L I C C C C R C C C C R \omega \omega \omega \omega \left( \right) \left( \right) = - \left( \right) + + + + + (26) $$

Xin通过将公式(26)代入公式(20)得到。然后根据公式(21)计算φ。并且

$$ p e s . t \varphi \omega = (27) $$

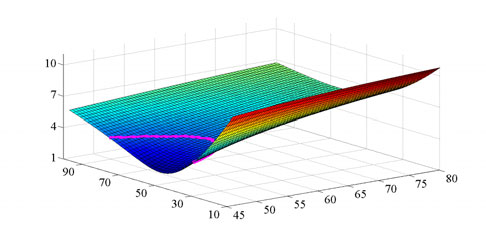
图8a中的三维图展示了tpe随n和Cp的变化情况，对应于公式(27)，而图8b中给出了根据公式(26)得到的Ls曲线。该设计流程可根据这些曲线细分为以下步骤：

步骤1 ：选择n和Cp。图8a中的紫色曲线包含tpe为4微秒的点。此处选择n为40，以便于计算，变压器匝数比较低，因此可以选择较小的Cp以从满载到轻载的施加电极电压范围较窄，如第2节所述。因此，Cp为52纳法。

步骤2 ：计算变压器漏感。图8b中的红色曲线表示当tpe为4微秒时，Cp和n之间的对应关系。因此，根据步骤1中确定的参数，Ls被确定为827 微亨。

步骤3 ：计算电流应力。根据公式(24)，在指定的n和Cp条件下，谐振峰值电流为1.94安，这有助于选择开关。

步骤4 ：检查Cp和Ls的误差容限。Cp受绕组结构及层间绝缘材料的影响较大（Shafiei et al., 2011）。此外，在高电压应用中，通常采用芯式变压器以获得高绝缘性能，而漏感难以准确计算（Doebbelin et al., 2008）。因此，Cp和Ls无法精确设计，需考虑误差容限。表3列出了当Cp和Ls变化10%时的关键参数。结果显示，当tpe固定为4微秒时，Cp和Ls的10%误差会导致额定功率出现约15%的偏差。然而，只需对工作频率进行不超过9%的微小调节，即可保证所需的额定功率，同时仍可实现零电压开关。因此，原型中Cp和Ls的微小误差是可以接受的。

tpe；(b) Ls)

表2 变换器规格

参数	数值
Pin	26 W
Cd	30 皮法
Cg	10 皮法
VT	2900 伏特
Vab	24 V
f s	20 千赫兹
tpe	4 μs

表3 当Cp和Ls变化10%时的关键参数

参数	Cp=52纳法, Ls=827微亨	Cp=47纳法, Ls=744微亨	Cp=57纳法, Ls=910微亨
	固定 tpe	固定 Pin	固定 tpe
Pin(瓦特)	26.0	23.0	26.2
Ir(安培)	1.94	1.78	1.91
f s(千赫兹)	20.0	22.3	21.8
tpe(μs)	4.00	4.06	3.28

4 仿真和实验结果

根据设计流程中获得的参数，制作了如图9所示的变压器样机，实际变压器参数列于表4中。磁芯由一对UF120A/70/30组成，该材料为锰锌铁氧体材料。

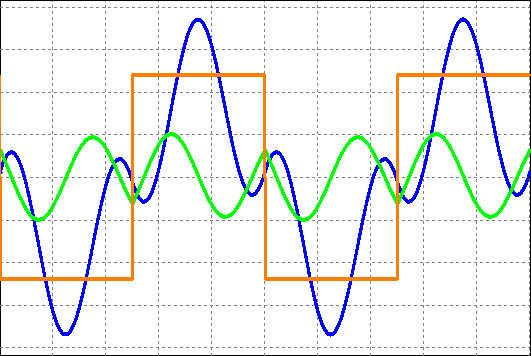
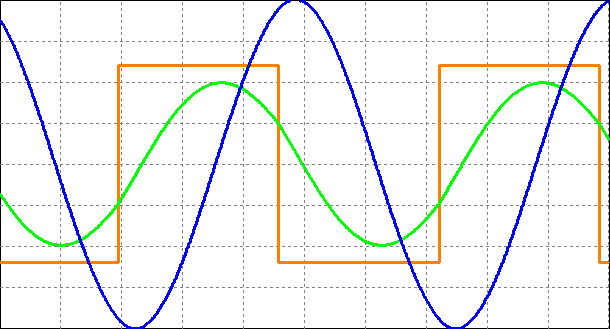
采用带有内置变压器的低功率DBD系统来验证等效电路和设计流程。实际计算中，Cp取54纳法，因为高电压探头（P6015，泰克）会引入折算到变压器原边的额外3皮法电容。次级侧（折算到变压器初级侧约5纳法）与负载并联，用于测量施加电极电压。图10a展示了忽略寄生电容时对应样机参数的仿真波形，该波形与图10d中的实验波形差异较大。因此，Cp对介质阻挡放电的性能影响显著，必须予以充分考虑。与实验波形相比，图1b所示带整流桥的变换器以及图4b所示带等效谐振模型的变换器的仿真波形分别如图10b和图10c所示。当电流从二极管换流至开关器件时，由于开关的导通电压和二极管的正向电压降，会出现电压降。表5列出了仿真、基于等效模型的计算以及实验的关键参数，结果验证了稳态分析和设计流程具有良好的准确性。

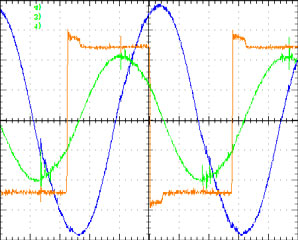
输出功率通过压电力显微镜进行调节，tpe是控制变量，通过自持振荡维持零电压开关（优素福和贾因，2007；吉尔伯特 et al., 2008）。图11a–11c展示了在不同频率下的实验波形，表明谐振槽路的输入功率随频率增加而降低，并且在整个功率范围内实现了零电压开关。当tpe大于10微秒时，施加电极电压过低，气隙中的放电几乎消失。表6给出了变换器的关键参数及其等效模型，与在不同频率下的实验结果进行了比较，验证了等效谐振槽路在不同功率水平下稳态条件的准确性。

由于RCFHA基于正弦谐振电流，等效模型的准确性在很大程度上受到谐振电流总谐波失真（THD）的影响。图12展示了额定条件下，实验谐振电流的谐波幅值相对于基波幅值的百分比。表7给出了通过仿真和实验波形得出的不同频率下谐振电流的总谐波畸变率（THD），结果表明，在通过工作频率调节功率的所有稳态条件下，RCFHA均具有较高的准确性。因此，该等效模型能够替代带整流桥的原始谐振变换器，从而简化性能分析和设计流程。

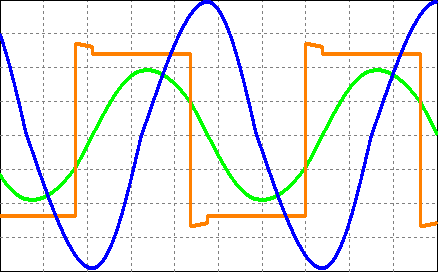
表4 变压器参数

参数	数值	设计	样机
n	40	40
Cp	52纳法	49 纳法
Ls	827 微亨	880 微亨

，图1b仿真的结果(b)，基于图4b等效模型仿真的结果(c)，以及实验结果(d))

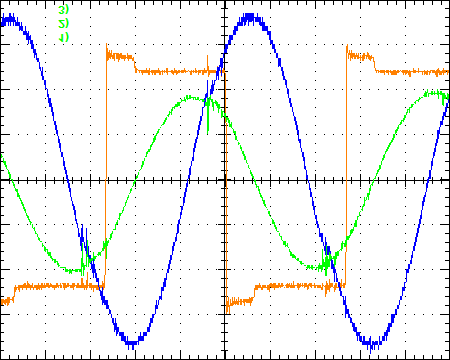，tpe = 8 μs (b) 和 tpe =10 μs (c))

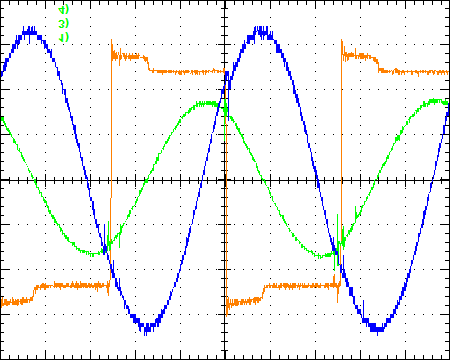
表5 额定条件下的仿真、计算和实验结果

参数	仿真与Cp	计算	实验
Pin(瓦特)	26.6	27.3	26.8
Ir(安培)	1.91	1.98	2.05
fs(千赫兹)	19.0	19.0	18.1
tpe(微秒)	4.03	3.91	4.00
Vae(千伏)	7.86	8.03	7.76

表6 不同频率下的计算和实验结果

tpe (μs)	Pin (瓦特)	fs (千赫兹)	Ir (A)	Vae (kV)
	计算结果	实验结果	计算结果	实验结果
6	23.3	23.0	19.6	18.7
8	15.4	15.3	20.7	19.6
10	4.59	4.53	21.8	20.7

表7 不同频率下谐振电流的总谐波失真（THD）

fs (千赫兹)	THD 仿真	THD 实验
18.1	3.16%	3.10%
18.7	2.29%	2.69%
19.6	1.40%	2.16%
20.7	2.62%	2.89%

5 结论

考虑了高升压变压器寄生电容的情况下，对用于低功率DBD的电源进行了研究。采用RCFHA进行稳态分析，并针对DBD负载的等效电路给出了详细推导。在低功率DBD应用中，寄生电容对变换器性能影响较大，在确定其数值时，应在小频率差与稳定的电极峰值电压之间做出折衷。设计流程根据推导出的表达式，采用磁集成技术设计了电源。最后，按照设计参数制作了带有两个平面电极的样机，实验结果与设计相符。