树莓派与FPGA控制德尔塔机器人

基于树莓派和现场可编程门阵列的并联德尔塔机器人系统控制器开发

摘要

本文提出了一种两轴“德尔塔工业机器人”的系统控制设计。该控制系统结合了嵌入式技术以及基于Linux操作系统的低功耗、低成本计算机“树莓派”。用户通过Linux图形用户界面与PC和现场可编程门阵列（FPGA）进行通信。FPGA作为专用硬件，为闭环伺服控制系统提供了高效率和灵活性。采用查找表方法以降低两轴德尔塔机器人相关运动学方程的计算复杂度。开发了Python程序用于创建和查询查找表。在两轴德尔塔机器人上进行了多项测试，系统测试结果中末端执行器的位置标准差在0.06毫米以内。

引言

有许多关于嵌入式系统用于控制各类机器人的介绍。许多此类嵌入式系统由ARM微控制器和现场可编程门阵列（FPGA）组合而成。采用这种方案的主要原因包括：微控制器能够轻松完成小数运算，FPGA具备独特的并行处理能力，这种组合方式可提供非常高效的控制系统。这降低了系统的复杂性，并实现了可重构控制架构，这对于控制各个工业机器人至关重要[1‐3]。例如，“双足机器人”需要简单小巧的控制器，目前主要采用数字信号处理器（DSP）作为主控制器，FPGA作为电机控制器，该方案为控制“双足机器人”提供了高效的方法[7]。另一种新方法是采用树莓派结合开源Linux操作系统来控制上述机器人。树莓派的低成本和低功耗显著降低了开发成本，并提供了与专用控制器相当的可靠控制系统[6]。

为了完全控制工业机器人的所有位置运动，必须计算所有移动机械部件的相关动力学方程，以确定所需的位置运动。然后将计算结果与工业机器人的实际位置运动进行比较。该方法反过来将有助于改进动力学方程，提高精度并加快计算速度。

有研究提出通过将计算数据与德尔塔工业机器人[4]的实际位置运动进行比较，来实现正向运动学计算。为了加快机器人操纵器的运动学计算速度，采用了查找表以及三角函数中正弦和余弦的相对角度。查找表中存储了带有系数的四阶级数，这些数据通过反三角函数和平方根函数计算得出。计算结果随后被输入到基于现场可编程门阵列的硬件平台，以实现极快的运算[5]。

本研究的目标是利用嵌入式技术和现场可编程门阵列技术，为典型的德尔塔工业机器人开发一种控制系统，以获得灵活性，提高响应速度和控制精度。现场可编程门阵列将用作专用控制硬件，树莓派将作为现场可编程门阵列的前端处理单元。该方法将提高效率，降低当前控制德尔塔工业机器人的复杂性以及耗时。

控制系统设计

相关动力学方程

来自《机械学报》中的“新型2自由度平移并联抓取机器人的概念设计与尺度综合”，以下是图1的相关动力学方程。

$$
H = l_1 \sin \theta_u + l_2 + h
\tag{1}
$$

$$
A \sin(\theta) + B \sin(\theta - \theta_u) + C = 0
\tag{2}
$$

$$
A = 2Hl_2 + h
\tag{3}
$$

$$
B = 2be + l_2
\tag{4}
$$

$$
C = \frac{b^2}{2} + \frac{h^2}{2} + eH + l_1^2 + l_2^2 - l_1 l_2
\tag{5}
$$

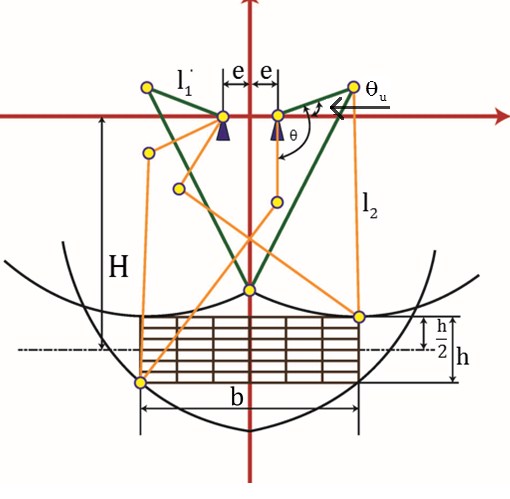
其中：
- $ H $：德尔塔机器人上臂旋转点到机器人工作空间中心点的垂直距离。
- $ e $：从中心点(0,0)到机器人各上臂旋转点的距离。
- $ l_1 $：机器人上臂部分的长度。
- $ l_2 $：机器人下臂部分的长度。
- $ \theta_u $：上臂相对于两个上臂起始旋转点之间连线的旋转角度。
- $ \theta $：德尔塔机器人的上臂的最大旋转角度。
- $ h $：德尔塔机器人的工作空间的宽度。
- $ b $：德尔塔机器人的工作空间的长度。

正向运动学

第一步，绘制一个典型的德尔塔机器人结构连接图，如图2所示，以简化机器人各部分的运动分析。第二步，在图2的结构连接上标出所有相关的数学变量，各个变量的具体细节如下：

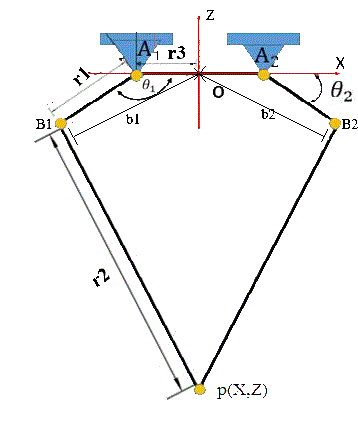
• A1 和 A2：德尔塔机器人的每个上臂的旋转点。
• B1 和 B2：德尔塔机器人的每个上臂末端的旋转点。
• b1 和 b2：B1 和 B2 旋转点的位置向量。
• $ \theta_1 $ 和 $ \theta_2 $：每个上臂在XZ平面上的旋转角度。
• O：XZ平面的原点(0,0)。
• r1：德尔塔机器人上臂部分的长度。(150) mm
• r2：德尔塔机器人下臂部分的长度。(403.11) mm
• r3：A1点与O点之间的距离。(50) mm
• p：德尔塔机器人的末端执行器的位置。

第三步：从机器人末端执行器的位置开始，基于位置向量 $ \mathbf{p} $（见公式(6)）推导正向运动方程。

$$
\mathbf{p} = (X, Z)
\tag{6}
$$

点 B1 和 B2 处的位置向量分别为 $ \mathbf{b}_1 $ 和 $ \mathbf{b}_2 $，如下所示：

$$
\mathbf{b}_1 = (r_3 + r_1 \cos \theta_1, r_1 \sin \theta_1)
\tag{7}
$$

根据 $ \mathbf{p} $、$ \mathbf{b}_1 $, $ \mathbf{b}_2 $ 的值，可得到其幅值：

$$
|\mathbf{p} - \mathbf{b}_i|^2 = r_2^2 \quad i = 1,2
\tag{8}
$$

由(7)和(8)可得方程(9)如下：

$$
(x - r_3 - r_1 \cos \theta_1)^2 + (z - r_1 \sin \theta_1)^2 = r_2^2
\tag{9}
$$

由方程(9)可得x的值如下：

$$
x = \frac{(2r_1 r_3 \cos \theta_1 - r_1^2 \sin \theta_1 \sin \theta_2 + r_3^2)}{(2r_1 r_3 \cos \theta_1 + r_1^2 \cos \theta_1 \cos \theta_2)}
\tag{10}
$$

设变量e和f如下：

$$
e = \frac{(r_1 \sin \theta_1 - r_1 \sin \theta_2)}{(2r_1 r_3 \cos \theta_1 + r_1^2 \cos \theta_1 \cos \theta_2)}
\tag{11}
$$

$$
f = \frac{(r_3 \cos \theta_1 + r_1 \cos \theta_1 \cos \theta_2)}{(2r_1 r_3 \cos \theta_1 + r_1^2 \cos \theta_1 \cos \theta_2)}
$$

因此：

$$
x = ez + f
\tag{12}
$$

将方程(9)代入方程(7)得到(13)如下：

$$
x^2(1-e^2) + z^2(-2ef + er_1 \cos \theta_1 + er_3) + … = …
\tag{13}
$$

设以下变量d、g、h如下：

$$
d = 1 - e^2
\tag{14}
$$

$$
g = -2ef + er_1 \cos \theta_1 + er_3
$$

$$
h = f^2 - r_2^2 + …
$$

因此：

$$
dz^2 + gz + h = 0
\tag{15}
$$

由公式(10)、(11)和(12)代入输入值得到两个z值，一个正值和一个负值。由于端点p（在图2中）位于z轴的负侧，因此选择z的负值。这意味着角度和z的值都必须为负角度。

逆运动学

重新排列方程(7)和(8)，分别得到方程(14)和(15)，如下所示：

$$
\theta_i = 2 \tan^{-1}(Z_i) \quad \text{where } i = 1,2
\tag{16}
$$

and

$$
Z_i = \frac{-b_i \pm \sqrt{b_i^2 - 4a_i c_i}}{2a_i} \quad \text{where } i = 1,2
\tag{17}
$$

其中

$$
a_1 = r_1^2 + r_3^2 + x^2 + y^2 - r_2^2
\tag{18}
$$

$$
b_1 = -2yr_1 - 2(x+r_3)r_1
$$

$$
c_1 = (x + r_3)^2 + y^2 - r_2^2
$$

$$
a_2 = r_1^2 + r_3^2 + (x - r_3)^2 + y^2 - r_2^2
\tag{19}
$$

$$
b_2 = -2yr_1 - 2(x - r_3)r_1
$$

$$
c_2 = (x - r_3)^2 + y^2 - r_2^2
$$

现场可编程门阵列中查找表的实现

为了获得各个查找表中的所有数据集，必须在Python程序中使用逆运动学方法计算机器人工作空间内末端点p(X,Z)的相应值。德尔塔机器人的上臂和下臂长度分别为：150毫米和403毫米。Z轴上的最大行程长度为200.03毫米。X轴上行程长度的最大值为536.65毫米。表1是根据相关的逆运动学方程创建的一个典型查找表。

位置 X, Z [mm]	查找表：臂部运动角度 $\theta_1$, $\theta_2$ [degree]
0.00, -350	0.00, 0.00
...........	.............
-140.00, -350	340.61, 37.45
...........	.............
-150.00, -350	340.12, 40.47

控制系统设计

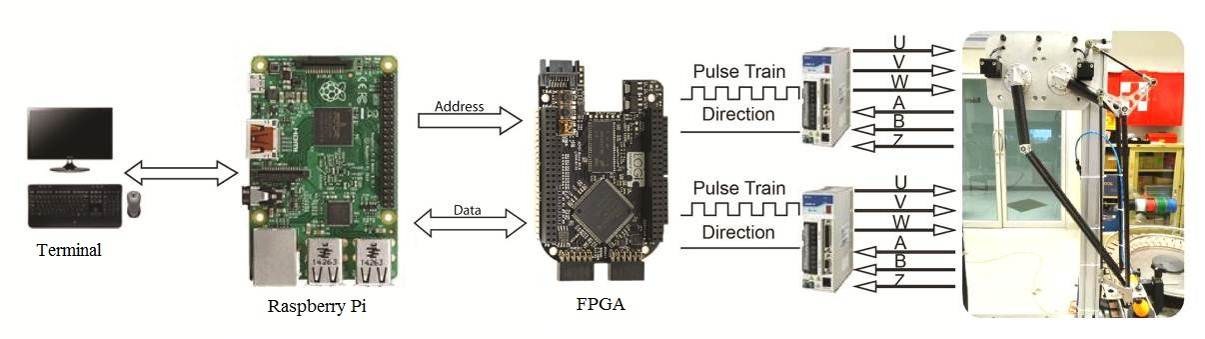
树莓派是一种低成本、低功耗的商用开发板，可选择支持开源的Linux操作系统。在图3所示系统中，更便于开发图形用户界面来控制专用的现场可编程门阵列。为了控制机械臂，树莓派通过地址/数据线向现场可编程门阵列发送一系列指令。根据接收到的指令，现场可编程门阵列硬件生成相应的脉冲信号，发送给交流伺服驱动器，从而驱动机械臂运动到指定位置。

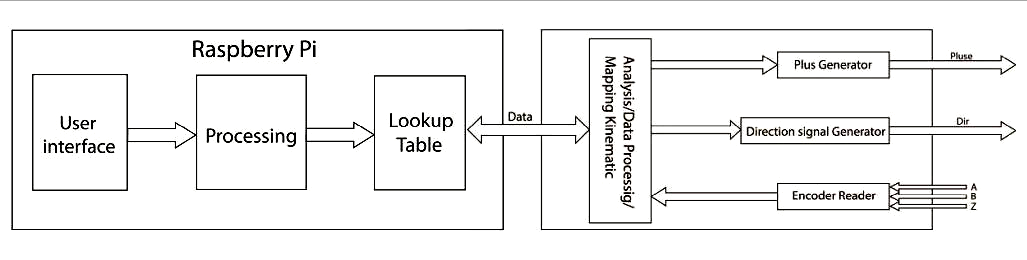
要控制机器人，主要有以下两个步骤：
树莓派通过图形用户界面与用户通信。查找表被用于减少机械部件运动的计算量。树莓派作为前端计算机，向现场可编程门阵列发送/接收数据。
现场可编程门阵列根据运动学过程分析接收到的数据，并将其转换为适当的脉冲序列格式，以实现更高精度的机器人运动，如图4所示。

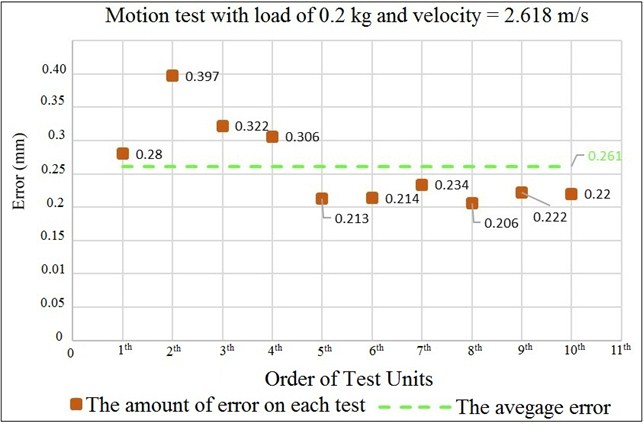
图5中的流程图是树莓派上控制程序的流程图和现场可编程门阵列上电机控制的流程图。

实验结果

控制德尔塔机器人的目标是通过控制X轴和Z轴的运动，使机械臂移动到所需的位置。实验按以下步骤进行：在XZ平面上对携带0.2千克负载的两轴德尔塔机器人从起点(0,0)到终点(300,0)以2.618米/秒的速度进行了多种测试，测试结果如图6所示。

从图6可以看出，测试的误差平均值为0.261毫米，标准差（S.D.）为0.06毫米。

摘要

在本研究中，我们提出了将树莓派和现场可编程门阵列结合用于两轴德尔塔机器人的嵌入式控制系统。测试结果表明，所提出系统的目标已达成。采用查找表方法确实降低了德尔塔机器人运动的计算复杂度。尽管测试过程中存在一些误差，但测试后的进一步分析表明，误差的主要来源是机器人机械部分的偏差。目前，研究实验室已在重新设计新型两轴德尔塔机器人。未来还将开展更多研究，以提升所提出嵌入式控制系统的性能。