高等数学：极限（零比零型、∞比∞型）

ok雷迪森and砖头们，废话不多说，今天我们讲的是极限。

目录

极限

一、极限小知识

1. 极限存在

2. 极限是什么

3. 做题步骤

4. 无穷分之C，零分之C

二. ∞比∞型（抓大头）

1. 幂函数抓大头

2. 指数函数抓大头

三、 0比0型

1. 公式

2. 注意事项

3. 对于一部分公式的记忆方法

4. 例题

四、扩展知识点极限

1. 零乘有界

---

极限

一、极限小知识

1. 极限存在

极限存在的条件：左右极限存在并且相等。什么，你问我极限是什么？？？，且随我前来。

2. 极限是什么

极限是指，某个东西A无限趋近某个东西B但是永远不能达到。好吧，我知道你可能没有看懂，让我们来看看下面这个图:

3. 做题步骤

（1）先把x趋向于x0中的这个x0带入到f（x）中定型。也就是把0带入到咱们的肉包子里面。

（2）定完型后，根据不同类型的极限使用不同的方法（稍后会介绍到方法。）

（3）定型时，可以将乘除关系中的非零常数先计算。（就是将x0带入到某个式子中，可以提前得出来一个常数）

tip:f(x)在某点x0处的极限值与f(x)在该点处有无定义f(x0)无关

4. 无穷分之C，零分之C

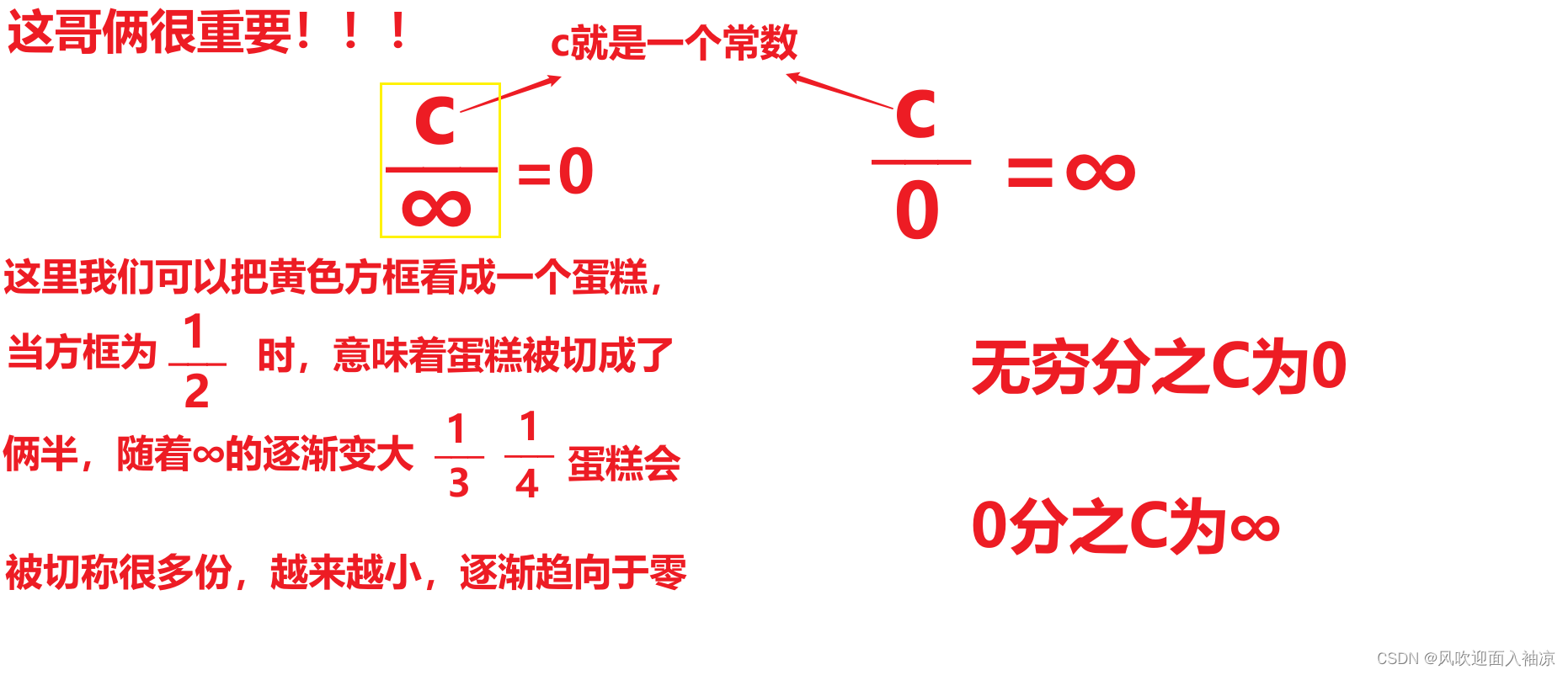
俗话说知己知彼，百战不殆。我们了解了它有哪些题型，还怕不会做？都是撒撒shui。

二、 ∞比∞型（抓大头）

按照咱们的做题步骤带入后分子分母都是无穷。

解法：抓大头

1. 幂函数抓大头

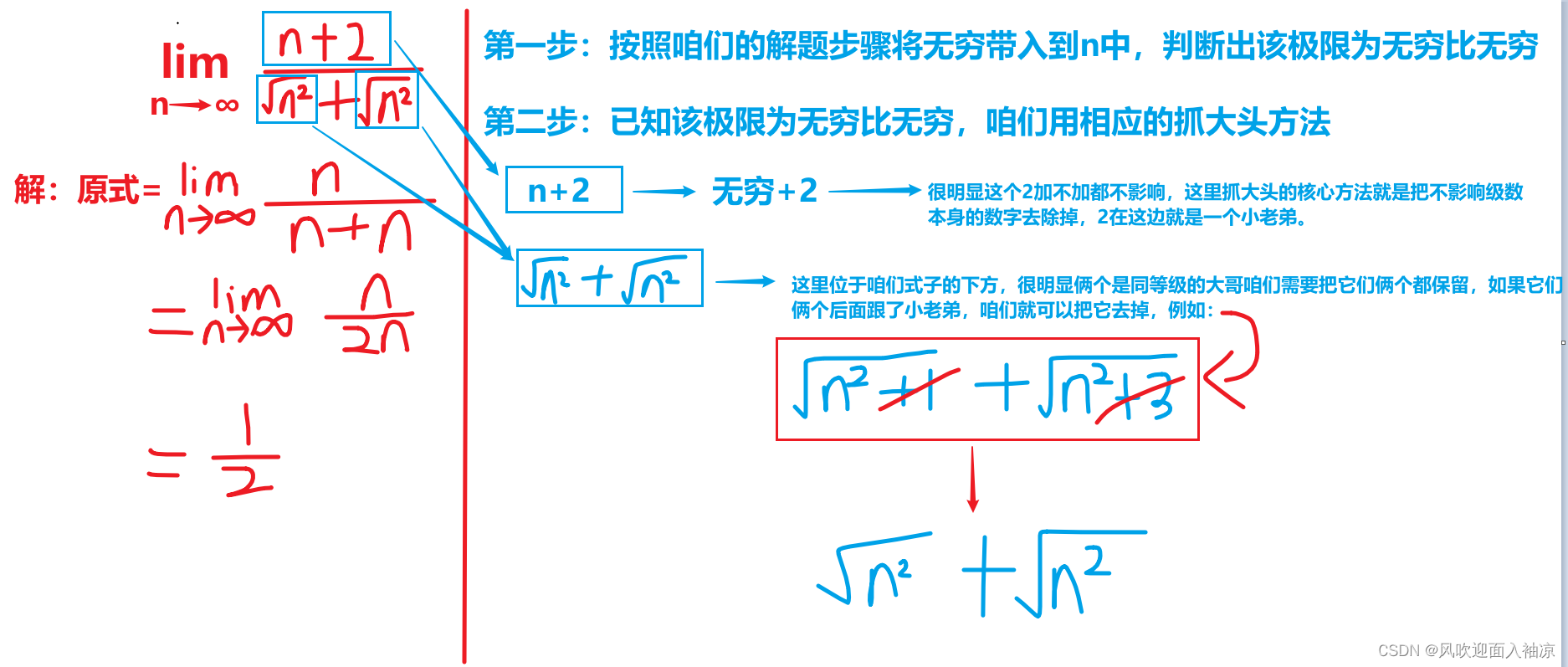
2. 指数函数抓大头

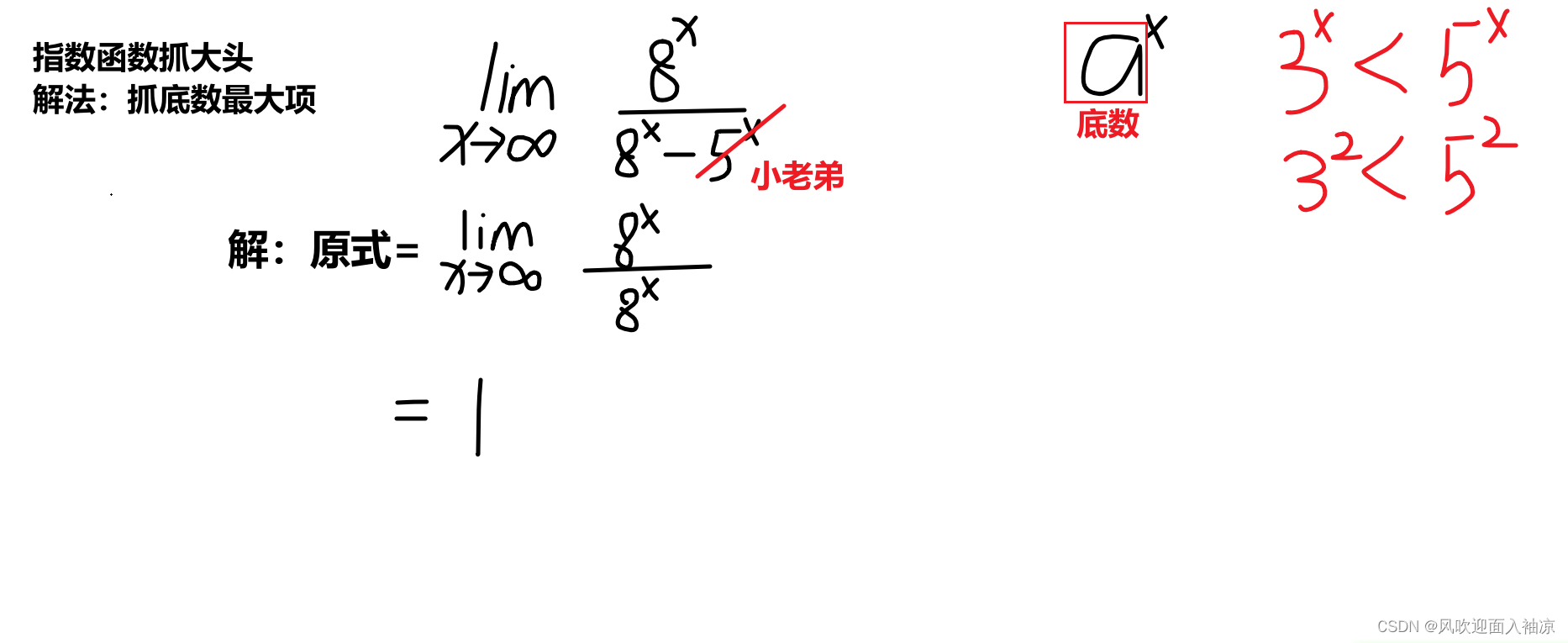
三、0比0型

按照咱们的做题步骤带入后分子分母都是0，下面的公式是需要记住的。

解法：用等价无穷小求解（在乘除中使用）

1. 公式

2. 注意事项

在加减中慎用等价无穷小。在专升本阶段的极限中，我觉得可以直接变为：在加减中禁用等价无穷小。例如下面的式子咱们是禁用的：

3. 对于一部分公式的记忆方法

其实是很简单的，只不过我描述的文字有点多了。。。不知道有没有解释清楚。

大家可以看到一共有五个函数，其实都是对应的。tanx对应arctanx，arcsinx对应sinx，中间则是一个单独的x，记住图像便可以不用记公式了-.-,我觉得公式记住了不常用就还是会忘掉，相反利用图像有些公式用的多了自然而然就记住了。

4. 例题

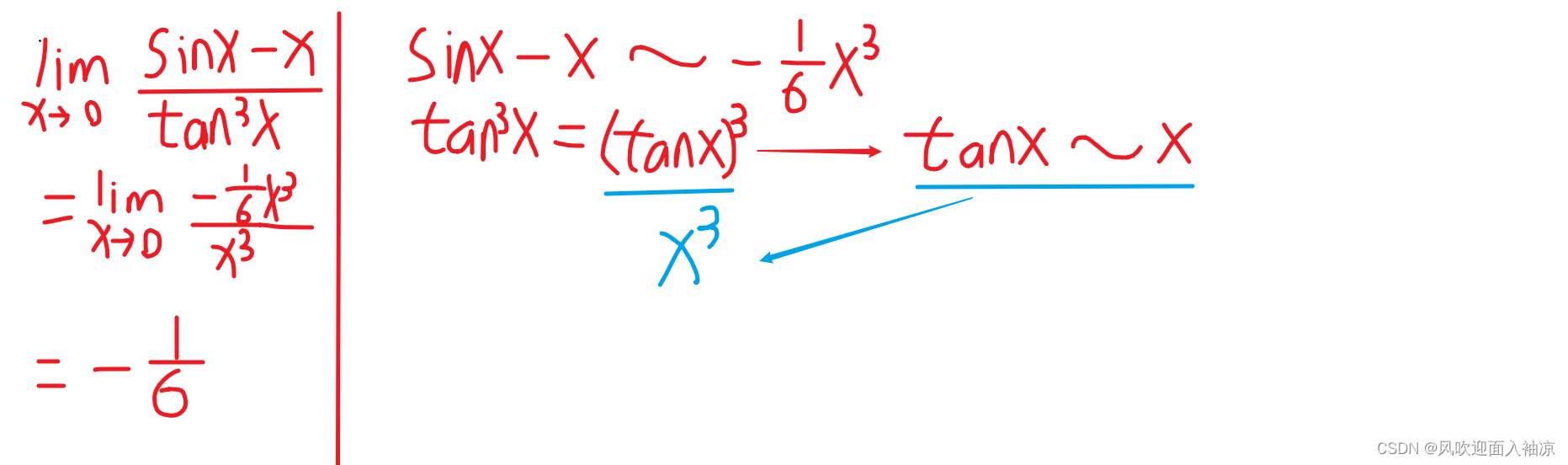
四、扩展知识点极限

1. 零乘有界

考点：遇到sin∞、cos∞、arctan∞优先考虑咱们的   0乘有界=0