HDU3944 （Lucas定理+阶乘逆元预处理）

最新推荐文章于 2024-08-12 01:43:46 发布

WayJasy

最新推荐文章于 2024-08-12 01:43:46 发布

阅读量371

点赞数

CC 4.0 BY-SA版权

分类专栏：数论文章标签： Lucas 预处理

本文链接：https://blog.youkuaiyun.com/pall_scall/article/details/95254073

数论专栏收录该内容

5 篇文章

订阅专栏

博客围绕杨辉三角中从顶点(0,0)走到给定点(n,m)的最小和问题展开。分n>=2m和n<2m两种情况给出答案公式，之后因有多组样例且n、m很大，需用Lucas定理对组合数进行预处理，包括对素数打表及对阶乘和阶乘逆元预处理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

$题意：在一个杨辉三角中，从顶点 (0, 0) 走到给定点 (n, m) 的最小和$
如图：
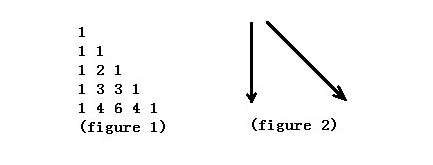
在这里插入图片描述
$①对于n大于等于>=2m时，如果走到(4,1),即C(mn)=4这个点，那么我们可以选择先一直往下走（取尽量多的1），然后走到与4成斜线时，往斜的方向走，因为越往下走值越大，直线走不了的时候走斜线一定是最优的。①对于n大于等于>=2m时，如果走到(4,1),即C\tbinom{m}{n}=4这个点，那么我们可以选择先一直往下走（取尽量多的1），然后走到与4成斜线时，往斜的方向走，因为越往下走值越大，直线走不了的时候走斜线一定是最优的。$

$n-m+C\tbinom{m}{n+1},就是取1的个数+斜线上的和$

$② 对于 n 小于 2 m 的情况，同理取尽量多的 1 ，那么肯定先走斜线，走到与目标值在同一竖线上时，直接往下走直线，其实和第一种情况是一样的。$

$此时答案就是m+C(n−mn+1)，取1的个数+竖线上的和此时答案就是m+C\tbinom{n-m}{n+1}，取1的个数+竖线上的和$

总结就是

$(n-m+C\tbinom{m}{n+1})\mod p，n>=2m$
$(m+C\tbinom{n-m}{n+1})\mod p，n<2m$

接下去就是如何处理这个组合数
$由于有多组样例，所以需要进行预处理。并且 n, m 很大，普通的阶乘逆元打表肯定不行了。这时候就要用 L u c a s 定理$

$f a c [j] [i] 表示在模第 i 个素数的情况下， j 这个数的阶乘$
$i n v [j] [i] 表示在模第 i 个素数的情况下， j 这个数的阶乘逆元$
$因为保证输入的模数是素数，所以先对 110000 的素数打表（有 t o t = 1229 个），然后对 f a c, i n v 预处理，最后套个 L u c a s$

#include<cstdio>
#include<iostream>
#define maxn 10010
#define ll long long
using namespace std;
int inv[maxn][1500],pri[maxn],num[1500],fac[maxn][1500],prid[maxn];
int n,m,p;
int tot = 0;
int id;
void getprime(){
    pri[1] = 1;
    for(int i = 2; i <= 10000; i++){
        if(pri[i] == 0){
            prid[i] = tot;
            num[tot++] = i;
            for(int j = i+i; j <= 10000; j+=i)
                pri[j] = 1;
        }
    }
}
int quickpow(int A,int B,int mod){
    A%=mod;
    int ans=1;
    while(B)
    {
        if(B&1)
        ans=(ans*A)%mod;
        A=(A*A)%mod;
        B>>=1;
    }
    return ans%mod;
}
void solve(){
    getprime();
    for(int i = 0; i < tot; i++){
        fac[0][i] = inv[0][i] = 1;
        for(int j = 1; j < num[i]; j++){
            fac[j][i] = (fac[j-1][i]*j)%num[i];
            inv[j][i] = quickpow(fac[j][i],num[i]-2,num[i]);
        }
    }
}
int CC(int n,int m){
    /*注意判断*/if(m>n) return 0;
    //注意取模 
    //费马小定理求逆元 
    return ((fac[n][id]*inv[m][id]%p)*inv[n-m][id]%p)%p;
}
int Lucas(int n,int m){
    if(!m) return 1;
    return CC(n%p,m%p)*Lucas(n/p,m/p)%p;//注意取模 
}
int main(){
    solve();
    int ca = 1;
    while(~scanf("%d%d%d",&n,&m,&p)){
        int ans;
        id = prid[p];
        if(n < 2*m) ans = m+Lucas(n+1,n-m);
        else ans = n-m+Lucas(n+1,m);
        printf("Case #%d: %d\n",ca++,ans%p);
    }
    return 0;
}