c++实现prim算法（最小生成树）

最新推荐文章于 2022-12-21 11:10:56 发布

原创

最新推荐文章于 2022-12-21 11:10:56 发布 · 3k 阅读

43 ·

CC 4.0 BY-SA版权

本文解析了Prim算法如何通过逐步添加边来构建最小生成树，以特定顶点开始，更新权值并维护最小代价路径。通过邻接矩阵操作，确保每一步选择都是当前未加入树中代价最小的连接。

解读代码：

1.
从图中任选任选一个顶点作为初始点开始寻找最小生成树，定义的lowcost数组用来存放顶点间的权值，初始化为初始顶点与其他顶点的权值，之后再将初始顶点在lowcost数组中对应的值置为0，代表此顶点已经纳入最小生成树中，此后每次lowcost数组中的值被置为0就代表该顶点已经纳入最小生成树。

2.
遍历找到lowcost数组中非0的最小值，输出该顶点再纳入最小生成树（在lowcost数组中置为0）。

3.
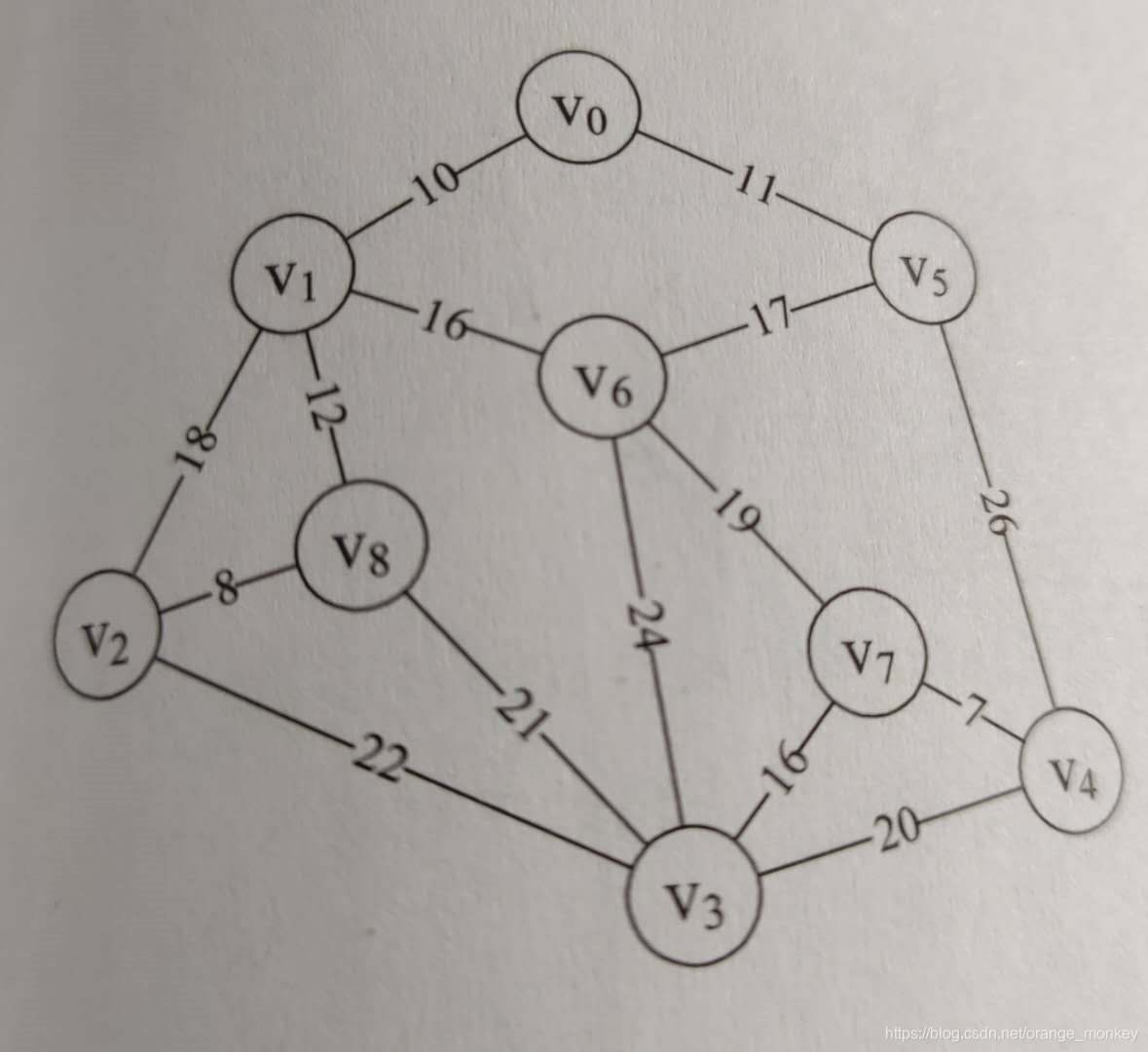
将刚刚纳入最小生成树的顶点与其他顶点的权值和lowcost数组的非0值比较，若前者有数值比后者小，就将小的数值赋给lowcost，此举是为了保证当前树中的顶点与其他顶点的权值最小，然后adjvex数组保存的是代价最小对应的顶点的下标，例如下图，假如以顶点v0为初始点，此时最小生成树（因为这时最小生成树就只有v0一个顶点，所以也也可以看成是v0到这三个顶点的权值）到v2,v8,v6的权值应该为无穷值，但是当v1纳入最小生成树之后，最小生成树到这三个顶点的权值就可以分别变为18，12，16（也可以看成是v1到这三个顶点的权值），所以此时adjvex数组下标为2，6，8的值就应该变为1，之后再用比较完的lowcost数组重复步骤2，直到所有顶点都纳入最小生成树为止。
在这里插入图片描述

代码：

#include<iostream>
using namespace std;

const int MAX = 10;
const int _INFINITY = 65535;  //初始化最小值为一个不可能的数值
class Graph
{
   
   
private:
	int vertex_num; //顶点数
	int edge_num; //边数
	int weight; //权值
	char vertex[MAX]; //顶点数组
	int edge[MAX][MAX]; //邻接矩阵
	int locate(char ch); //定位

public:
	Graph(int v_n, int e_n); //构造函数
	void print_graph(); //打印
	void prim(char ch); //prim算法
	char get_leter(); //获取字母
};

//定位（找到字母的下标）
int Graph::locate(char ch)
{
   
   
	int index;
	for (index = 0; index < this->vertex_num; index++)
	{
   
   
		if (this->vertex[index] == ch)