蓝桥杯--数论1 AcWing 1295. X的因子链 （算术基本定理，线性筛）

AcWing 1295. X的因子链

输入正整数 X，求 X 的大于 1 的因子组成的满足任意前一项都能整除后一项的严格递增序列的最大长度，以及满足最大长度的序列的个数。
输入格式
输入包含多组数据，每组数据占一行，包含一个正整数表示 X。
输出格式
对于每组数据，输出序列的最大长度以及满足最大长度的序列的个数。
每个结果占一行。
数据范围
1≤X≤220
输入样例：
2
3
4
10
100
输出样例：
1 1
1 1
2 1
2 2
4 6

题意：给出一个数n，求出在它除了1的因子中，能够倍乘的最长序列的长度以及最长序列的个数

经典数论题，涉及到算术基本定理和素数打表两个方面

---

算术基本定理

对于任意一个正整数n，可以将它分解成n个质因子的乘积

36 = 2 * 2 * 3 * 3
20 = 2 * 2 * 5
105 = 3 * 5 * 7

换句话说可以表达成如下形式，即P为一个质因数，a为他的指数

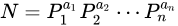
例如

36 = 2² * 3²
20 = 2² * 5¹
105 = 3¹ * 5¹ * 7¹

这个分解式具有存在性和唯一性，即每个大于1的自然数都可以如此分解，且这个分解式是唯一的，这个分析比较复杂这里不再赘述

可以观察出，n的每个因数即是n的各个质因数乘积的各种组合，如果想要获得一个倍增的因数序列，那么对于序列中的一个因数ki来说，ki+1应该是k乘上一个未使用的质因数

例如对于n=20来说，当序列第一个数是2时，那么第二个数则应该是22或25，才能满足即是20的因数，同时倍增

那么对于这个序列来说，如果想要长度最长，则应该让第一个数为一个质因数，第二个数为另一个质因数乘上第一个数，第三个数为另一个质因数乘上第二个数…以此推至最后一位

可见该序列的长度是与n的质因数数量有关的，如果n有4个质因数p1,p2,p3,p4，那么最大长度序列则应该是

p1，p1 * p2 ，p1 * p2 * p3， p1 * p2 * p3 * p4，

即因数序列最大长度即是质因数的个数

另一方面对于数量的计算，虽然序列中的每个数都是一个乘积，但实际变化的只是当前位置的质因数，可以简化为4个质因数的组合，找到这4个质因数在序列中位置的不同组合，即排列组合中的A ⁴₄ 运算或4!阶乘运算

同时，当一种质因数在全部质因数中多次出现时，则要除上重复部分

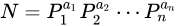
因此，根据下图a1,a2,a3…分别是各个质因数的个数情况下来计算，可以求出最长序列即是

(a1+a2+…+an) ! / a1!* a2! … a3!

---

线性筛求素数

根据上方的推理，还需要做的即是求出n的质因数分解式，需要对1~n的质数打表

如果使用对每个数都进行循环判断是否是质数的话时间复杂度会爆表，这里使用线性筛、也称欧拉筛的方法以O（n）的复杂度将素数打表，同时可以记录下来每个数的最小质因数

代码如下

	static int primes []=new int [N];//素数表
	static int minp[]=new int [N];//下标数的最小质因数
	static boolean st[]=new boolean [N];//判断是否为素数，false则为素数，true为合数
	static int cnt;//素数个数
	
	static void get_primes(int n) {
		for(int i=2;i<n;i++) {
			//如果i是素数，则它的最小质因数是它本身，同时记录进素数表
			if(!st[i]) {
				minp[i]=i;
				primes[cnt++]=i;
			}
			//循环对后方合数进行处理，判出条件为合数在N内
			for(int j=0;primes[j]*i<=n;j++) {
				int t=primes[j]*i;//待处理合数
				minp[t]=primes[j];//记录该合数的最小质因数
				st[t]=true;//合数标记
				if(i%primes[j]==0) {//核心代码
					break;
				}
			}
		}
	}

这里理解的还不是很透彻，不过个人理解核心代码大致意思是，当 i 可以将primes[j]整除时，那么后方由 i 组成的合数将会被更大的合数（i*primes[j]或以上）筛去，而不必在现在就筛除，即对于每个合数k来说，它只会被它的最小质因数筛去，而这个过程会在最接近k时产生

例如

40=2 * 20=4 * 10=5 * 8

只有当i=20时，40才会被唯一一次筛除即20*2，获得它的最小质因数2，而在4 * 10或5 * 8时则不会被筛除

这样做的目的是，确保每个数只会被标记一次，而不是在2 * 20=4 * 10=5 * 8这三种情况时每次都被标记，避免造成时间上的浪费，也正是这句核心代码才能保证线性筛以O(n)的时间复杂度实现

---

代码如下

import java.io.*;
import java.util.*;

public class Main {
	static Scanner tab = new Scanner(System.in);
	static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
	static int N = (1 << 20) + 10;

	static int primes []=new int [N];
	static int minp[]=new int [N];
	static boolean st[]=new boolean [N];
	static int cnt;
	
	//素数打表
	static void get_primes(int n) {
		for(int i=2;i<n;i++) {
			if(!st[i]) {
				minp[i]=i;
				primes[cnt++]=i;
			}
			for(int j=0;primes[j]*i<=n;j++) {
				int t=primes[j]*i;
				minp[t]=primes[j];
				st[t]=true;
				if(i%primes[j]==0) {
					break;
				}
			}
			
		}
	}
	
	public static void main(String[] args) throws IOException {
		get_primes(N-1);
		int sum[]=new int [N];//记录某个质因子的个数即ai
		while(tab.hasNext()) {
			int x=tab.nextInt();
			if(x==-1) return ;
			int k=0;//质因子种类数
			int tot=0;//质因子总数
			while(x>1) {
				int p=minp[x];//取出最小质因子
				sum[k]=0;//重置sum
				while(x%p==0) {//当x中还存在p时
					sum[k]++;//质因子p数量+1
					tot++;//质因子数+1
					x/=p;//x更新
				}
				k++;//质因子种类数+1
			}
			long res=1;
			for(int i=1;i<=tot;i++) {//计算分子阶乘
				res*=i;
			}
			for(int i=0;i<k;i++) {//除去分母阶乘
				for(int j=1;j<=sum[i];j++) {
					res/=j;
				}
			}
			System.out.println(tot+" "+res);
			
		}
		
	}
}