元启发式算法在对称密钥设计中的应用

如何使用元启发式算法进行对称密钥原语的设计

1 引言

近年来，我们见证了用于对称密钥原语自动分析的计算机工具的重大发展。这些工具涵盖了广泛的分析技术：差分[5–7,16,18,19,21,30–33,38–40],线性[17,30],不可能差分[12,15,26,29,36,43],中间相遇[8,14,15],等。这些工具有多种应用，其中之一便是作为新设计安全性的证明，因为它们能够提供新设计对大多数（有时是全部）已知密码攻击的抵抗能力。

然而，用于对称密钥原语设计的高级计算机工具尚未被考虑。相反，大多数设计问题要么通过解析方法解决，要么使用诸如暴力破解和随机搜索等简单的计算机算法来解决。例如，考虑调整高级加密标准（AES）以使其更抵抗中间相遇攻击的问题。借助针对中间相遇攻击的自动化分析工具，我们可以检查每个调整后AES版本的安全裕度。如果我们仅调整行移位（ShiftRows），则可以通过暴力破解所有可能的调制参数空间，利用上述自动化工具对每种调制参数进行检查，并找出能提供最高安全性的那一个。另一方面，如果我们决定同时调整行移位（ShiftRows）和列混淆（MixColumns），那么调制参数的空间将对于暴力破解来说可能规模过大，因此我们将采用随机搜索。也就是说，我们 将仅检查一部分随机选择的调制参数，并从中找出最佳的一个。这两种简单的 算法基本上是设计者唯一可用的计算机工具。

假设目标是创建一种用于对称密钥原语自动设计的工具，该工具需满足以下两点：（1）基于更先进的搜索方法；（2）具有通用性，能够应对多种设计问题。需要注意的是，暴力破解和随机搜索不满足第一点，因为它们过于简单，但满足第二点，因为它们可应用于多种设计问题。简而言之，这两种算法是最简单的优化方法。因此，为了构建更优的设计工具，我们需要关注下一类已知的优化算法，这类算法不仅通用，而且更为复杂，即元启发式算法。

元启发式算法是一种用于寻找优化问题足够优解的搜索算法。它对被优化（目标）函数几乎不做任何假设，即使函数未被明确定义但可以进行查询时，它也能表现良好。元启发式算法中实现的搜索策略通常基于某种仿生方法或技术——元启发式算法以其对应的自然现象命名，例如粒子群优化、模拟退火、蚁群优化、进化计算等。在密码学中，元启发式算法主要用于设计满足特定准则的S盒，例如抵抗密码攻击[1,11,34,42,44]。

我们的贡献. 可以认为，对任何对称密钥密码学原语的各个部分的设计决策，都是以优化为目标（如安全性、尺寸、吞吐量等）。因此，我们将设计问题纯粹视为一个优化问题。用于解决该优化问题的计算机算法，我们称之为自动设计工具。

我们的工具基于元启发式算法。这些搜索算法具有足够的通用性，能够解决大多数设计优化问题。我们使用了两种受自然启发的元启发式算法：模拟退火和遗传算法。我们在第2节中介绍这些元启发式算法；对每种算法，我们指出其主要思想，提供伪代码描述，并列出最重要的参数。在第3节中，我们将元启发式算法应用于解决两个具体的设计优化问题。为此，我们首先确定优化问题，然后对其进行形式化定义（描述目标函数及其输入空间），最后使用元启发式算法寻找良好解。我们的两个问题与最近提出的分组密码SKINNY[3]以及基于 AES轮的构造 [23]中寻找新组件相关。我们选择这两种原语是因为它们最能展示元启发式算法的有效性。无论是SKINNY还是AES轮结构，其设计都具有明确的优化目标，并且鉴于其出色的性能，已实现了这些目标。然而，元启发式算法可以实现进一步的优化。我们展示了模拟退火和遗传算法可用于在这两种原语中寻找特定组件从而根据设计者认为重要的标准获得更高的性能。更准确地说，我们使用元启发式算法为SKINNY寻找密钥扩展调度中的一个置换，以提高对相关密钥扩展攻击的抵抗能力；对于AES轮结构，则用于寻找一种轮变换，以增强对内部碰撞的安全性。

总之，我们的主要目标和贡献是提供实证证明：由于元启发式算法的简单性和通用性，它们可能是对称密钥原语自动设计中最有效的工具。

2 元启发式算法

考虑一个简单的优化问题：求目标函数 f(x) : D → R的最优值（最大值或最小值）。如果 f(x)以黑盒形式给出，即可以进行查询但没有显式定义，则无法应用数学和标准计算机科学方法来解决该优化问题，因为这些方法要求 f(x)有完整的定义。此外，如果定义域 D是离散的且尺寸很大，则该优化问题无法在实际时间内通过暴力破解解决。

为了应对这类问题，我们使用元启发式算法。它们是近似算法——所提供的解不能保证是最优的（尽管某些算法具有渐近收敛的理论证明）。然而，元启发式算法仅使用有限的计算资源就能输出解，即它们是实用的算法。因此，除了其他应用之外，元启发式算法非常适合用于搜索那些目标函数（黑盒）计算代价较高的优化问题的近似最优解。

元启发式算法有多种分类方式。根据搜索策略，它们可分为局部搜索（仅尝试寻找局部最优）和全局搜索（全局最优）。例如，最流行的元启发式方法之一是爬山法，它仅尝试寻找局部最优。另一种分类是单点与基于种群的搜索。单点元启发式一次只处理一个候选解，而种群式方法则同时处理多个候选解。爬山法、模拟退火、迭代局部搜索是单点搜索的例子，而遗传算法、蚁群优化则是种群式搜索的例子。

通过比较元启发式算法解决某些知名问题所需的时间复杂度（以对 f(x)的调用次数衡量），可以实验性地测试其效率。根据问题的不同，两种元启发式算法的相对效率可能会有所变化，即对于某些问题第一种可能更优，而对于其他问题则第二种更优。因此，“最佳元启发式算法”这一术语没有意义。测试元启发式算法的效率并非易事，因为每种算法都关联着一组参数。针对每个具体问题，元启发式算法都需要对其参数进行精细调整——这可能是一个非常漫长且繁琐的过程，但会对算法的效率产生重大影响。对于每种元启发式算法，都有是其参数推荐的一组取值，然而这些取值是从先前应用中通过经验推导得出的，因此不能保证最优性。

接下来，我们将使用两种元启发式算法：模拟退火和遗传算法。这一选择并非偶然——据报告，它们分别在单解式和种群式类别的多种问题上表现最佳。下文将简要介绍这两种元启发式算法，我们相信这足以帮助理解后续的思想。感兴趣的读者可以在[37,41]中找到有关元启发式算法的更多细节。

2.1 模拟退火

模拟退火[9,27]是一种单解式、全局搜索元启发式算法。它是一种仿生算法，模拟化学物质中发生的物理过程：加热后冷却并结晶。

给定一个目标函数 f(x)，模拟退火通过迭代改进潜在解来尝试找到其最大值1 。也就是说，从某个随机的 x0 开始，它构建 x1, x2,…。在第 i 次迭代中，xi 的值由前一个值 xi−1 生成，目标是进一步最大化函数 f(x)，即 f(xi) ≥ f(xi−1)。模拟退火的主要思想是允许解的概率性退化，即有时即使 f(xi) < f(xi−1)也接受 xi。然而，接受概率是变化的：在早期阶段（当 i 较小时）接受更多退化解，而后期则较少。这种策略允许算法在开始时探索更多种类的解，包括退化解，而在后期则专注于局部优化。注意，退化解使算法能够逃离局部最优。

模拟退火的正式描述见算法1。它接收三个参数作为输入：初始温度 T、冷却方案函数α(T)以及邻域函数 ε(x)。在初始化阶段，它为 f(x)的最大化问题随机赋值一个最优解 x。然后通过重复相同的步骤不断尝试构造更优的解：从 x生成一个新的候选解 x′，如果满足特定条件，则接受其作为新的解 x。函数 ε(x)通过对 x的值进行微小改变，从 x生成x′。如果 x′比 x更优，则将 x更新为 x′。然而，如果 x′更差，则不会立即拒绝，而是以一定的概率被接受。接受概率（用r< e f(x′)−f(x) T ,表示，其中 f(x′)− − f(x)为负数）在温度T较高且新候选解 x′的目标函数值接近旧候选解 x时更高。当满足终止条件时，迭代停止。该条件可设置为不同的形式：如迭代次数、温度值等。

1类似地，通过一些微小的改动也可以实现最小值的寻找。2例如，当 x是一个向量时， ε(x)将返回在某个预定义的ε环境中 x的另一个向量。

算法1. 模拟退火

输入： 温度 T0，冷却方案 α(T)，邻域函数 ε(x)
x ←$ 生成随机初始值
T ← T0
do
x′ ←− ε(x) 生成随机邻居
如果 f(x′)> f(x)那么 如果新最大值，则接受它
x ← x′
else
r ← U[0, 1] 生成均匀的随机数
如果 r< ef(x′)−f(x) T then
x ← x′ 接受劣化解
结束如果
结束如果
T ← α(T) 降低温度
while(终止条件未满足)
输出: x

参数。 如前所述，选择参数值时的主要目标是优化该元启发式方法的效率，使其能在尽可能短的时间内产生接近全局最大值的解。模拟退火需要以下参数：

–邻域函数： ε(x) 应返回 x′位于x邻域内的解，即 ‖x − ε(x)‖的差异应较小。例如，若 x是一个向量，则可将 ε(x) 定义为仅在一个坐标上与 x不同的向量。注意，如果 ‖x−ε(x)‖较大（或无限制），则模拟退火退化为普通的随机搜索。更多关于邻域函数的讨论参见附录B。

– 冷却方案： α(T) 应为单调（严格递减）函数。 α(T) 有多种选择：线性、指数、逆向、对数及其他冷却方案。我们将使用逆向冷却，定义为 α(T) = T 1+βT，其中 β 是一个较小的常数，通常为0.001 数量级。我们选择逆向冷却，因为在初步实验中其表现优于其他冷却方案。

– 初始温度： 如果 T0 较高，则模拟退火将探索更多的可能性，但需要更长时间才能收敛到接近最优的解。相反，较低的初始温度会导致更快地找到某个可能并非最优的解。 T0 的值应根据 ε(x) 和 α(T) 的取值以及允许的时间复杂度来选择，以在探索更多解的可能性与最大允许时间之间取得平衡。

2.2 遗传算法

遗传算法 [22]是一种种群式、全局搜索元启发式算法。它属于进化算法这一更大类别的算法，通过模拟自然选择来求解优化问题。

Algorithm 2. 遗传算法

输入: 种群大小 N，选择函数 Selection({Fi})，交叉 func‐ 变换 Crossover(PA, PB)，变异概率 MutationProbability 和函数 Mutate({Ci})
对于 i=1到 N 执行
Pi ←$ 生成随机父代
结束循环
do
for i=1到 N do
Fi ← f(Parenti) 计算父代的适应度
end for
for i=1到 N 执行
2
(PA, PB) = Select({F}) 选择2个父代
(C2i, C2i+1) ← Crossover(PA, PB) 生成2个子代
结束循环
对于 i=1到 N 执行
r ← U[0, 1] 生成均匀分布的随机数
如果 r< MutationProbability 那么
Ci ← Mutate(Ci) 变异 子代
结束 如果
结束 对于
{Pi}←{Ci} 更新 代
while(未满足终止条件)
输出： {Pi} 中的最优父代

为了找到目标函数（称为适应度函数）的最大值，遗传算法通过迭代（称为代）进行工作。在每次迭代中，它尝试改进一组解，而不是单个解。该组被称为种群的个体。为了从旧种群产生新种群，即更替代，遗传算法使用两种操作：变异和交叉。变异应用于一个个体，包括对其轻微改变。另一方面，交叉是繁殖的同义词。它选取两个个体（称为父代），并产生两个新个体（称为子代）3。父代的选择由所谓的选择函数控制，该选择函数决定如何选择父代。选择函数偏向于存在一些交叉算子的变体，其中两个父代可以产生一个或超过两个子代。

适应度更高的个体（适应度函数值更高）。这样做是为了模拟自然选择中的父代选择——具有更好品质（基因）的个体有更高的繁殖机会。遗传算法的形式化描述见算法2。

参数。 遗传算法使用大量的参数：

– 种群大小 N：个体的数量。推荐的N值范围为 [log |D|,2 log |D|]，其中 |D| 是搜索空间的尺寸。

–选择函数：最流行的几种选择方式包括轮盘赌选择（个体被选为父代的概率与其适应度函数成正比）、锦标赛（首先随机选择若干个体，然后根据其适应度值以类似锦标赛的方式选出优胜者）、排名（根据个体的适应度值进行排序，并以其位置——即排名——来确定其被选择的概率）以及随机选择（根据概率分布同时选择若干个体作为父代）。更多关于选择函数的详细描述见附录B。

– Crossover function：它生成的子代会与父代具有相似性。例如，如果将两个父代表示为向量（这些向量的坐标称为基因），则其子代向量的相应坐标值将取自第一个或第二个父代4。交叉函数决定子代如何继承父代的基因。我们将使用均匀交叉函数，即子代的每个基因（向量的每个坐标）来自任一父代的概率相等，且该概率与之前的基因无关。

– 变异概率和函数：在一代中，变异仅应用于由变异概率定义的少数个体。该概率的推荐范围是[0.001, 0.01],，即仅有大约0.1–1%的个体发生变异。变异函数定义了个体如何被改变——它会轻微地改变个体的基因。

– 精英策略：通常每一代中的最优个体都会被保留下来，即在每一代结束时，一定比例的最优父代会进入下一代（被复制到子代中）。这被称为精英策略 （来自“精英”一词）。建议的精英策略范围为[0.05–0.2], ，即适应度最高的5%至20%的父代进入下一代。

3 应用

通常，一个新的密码学原语的目标是至少在一个功能上优于所有已知的设计。该功能可能有所不同，可能包括更高的吞吐量、更小的占用空间、更高的安全性等。无论选择何种功能，设计者的目标本质上都可以视为一个优化问题。

密码设计的优化问题可能可以使用元启发式算法来解决，也可能不可以。如果优化问题过于宽泛或目标函数没有明确定义，则元启发式算法无法解决问题。例如，试图以某种方式调整高级加密标准的轮函数以最大化其对不可能差分攻击的抵抗力，并不能构成一个良好的目标函数。另一方面，通过更改系数来调整列混淆矩阵，则提供了明确的目标函数：该函数的输入是某个列混淆矩阵，输出是针对不可能差分攻击的安全级别5。某些优化问题使用其他方法（如启发式算法甚至暴力破解）可能比使用元启发式算法解决得更好（更快或更精确）。例如，尝试调整高级加密标准中的行移位常数以最大化其对不可能差分攻击的抵抗力，由于所有可能变体的数量较少，因此只需暴力破解即可解决。

从上述讨论可知，我们可以在以下情况下使用元启发式算法来设计或改进对称密钥原语：

1. 优化目标可以量化（目标函数明确且可在任意输入上计算），2. 搜索空间相对较大，无法通过暴力破解覆盖，3. 解不一定需要是全局/局部最优（注意，启发式方法可能在可行时间内返回最优解，也可能不返回）。

接下来，我们给出两个适合使用元启发式算法解决的优秀优化目标示例。它们分别涉及提升SKINNY和来自[23]的基于AES轮的构造的安全裕度6。这两种原语是测试元启发式算法有效性的理想候选对象，因为它们是近期的设计，对组件优化有很强的关注，并且具有明确的优化目标。需要注意的是，我们也曾考虑将元启发式算法应用于其他几种近期设计，但由于各种原因，我们省略了这些应用的细节。例如，Simpira v2[20]和哈拉卡 [28]函数的潜在优化可以通过暴力破解来解决，因此该优化不满足上述第二个要求，故元启发式算法并非首选。另一方面，可以在认证加密方案Deoxys [25]中使用元启发式算法优化组件，但该问题与后续分析的SKINNY问题过于相似，因此我们予以省略。

假设可以计算在调制参数化的列混淆矩阵下对不可能差分攻击的安全级别。然而，我们提醒读者，这并不是元启发式算法的唯一用途——它们还可以用于优化设计的吞吐量、尺寸等方面。

3.1 SKINNY

SKINNY[3]是在CRYPTO’16上提出的一类分组密码算法。其目标是在硬件和软件实现方面与美国国家安全局的密码算法SIMON相当，同时提供更高的安全性。这些密码是可调式的，即除了密钥和明文外，它们还有一个称为调制参数的第三输入。调制基于一个框架[24]，该框架将密钥和调制参数统一处理，作为一个单一输入称为调制密钥。

SKINNY密码的状态大小为 n= 64或 n= 128比特，被视为半字节的 4× 4矩阵。另一方面，调制密钥大小 t是状态大小 n的倍数，并有三个版本： t= n、 t= 2n、 t= 3n。

SKINNY是迭代置换‐代换密码。在图1中，我们给出了当 t= 3n时密码 算法的一轮结构。一轮状态变换包含五个熟悉的步骤：SubCells是S盒层， AddConstants异或常数，AddRoundTweakey将每个tweakey字的前两行与状态的前两行进行异或，ShiftRows对状态行中的半字节进行移位，MixColumns将状态列乘以某个矩阵。在调制密钥调度中，三个tweakey字 T K1、T K2和 T K3经历两种变换：按状态的半字节置换 PT（对所有调制密钥相同）和按半字节的线性变换 li。

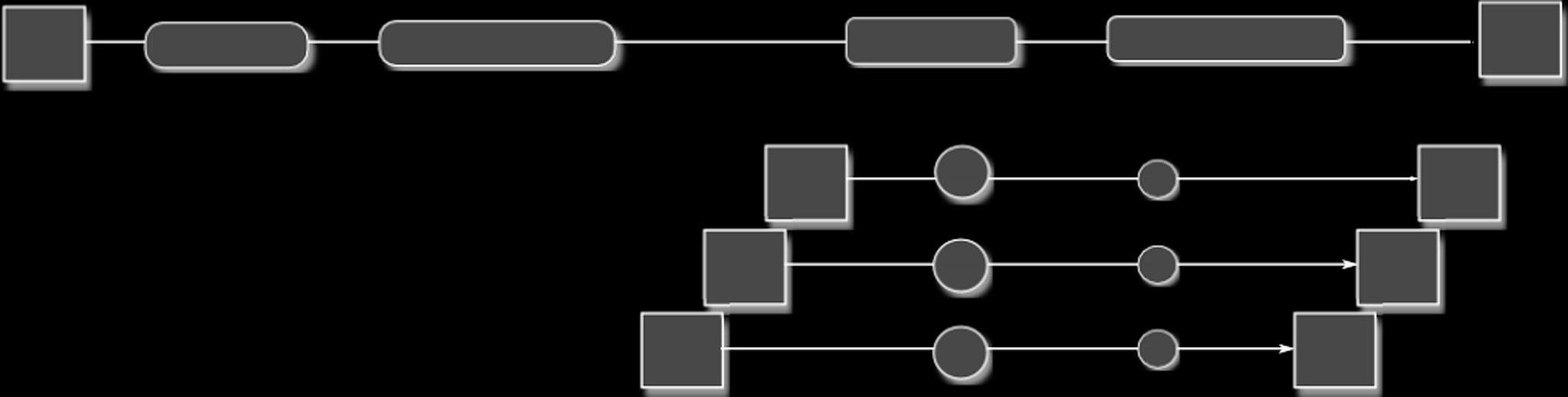
为了在硬件和软件上具有竞争力，SKINNY密码算法已得到高度优化。密码中使用的大多数变换根据某些设计准则具有高于平均水平的性能，并且是通过某种启发式方法或计算机搜索找到的。根据提交文档的扩展版本 [4],调制密钥调度中使用的半字节置换 PT“被选择以最大化活跃S盒数量的界⋯⋯在相关调制密钥模型中”。用于寻找 PT的方法未指定。

通过使用元启发式算法，我们将进一步优化 PT。需要注意的是，该优化问题已经得到了很好的表述：寻找PT以最大化最佳相关调制密钥特征中的活跃S盒数量。为了针对特定的 PT选择求得该数值，正如设计者所建议的，我们使用基于整数线性规划（ILP）的自动化工具。因此，ILP可以可以被视为目标函数 f，它以置换 PT 作为输入，并返回活跃S盒的数量。因此，我们的问题就变成了

max
PT
f(PT),

其中PT是一个16个元素的置换，附加约束条件为：前八个元素只能映射到后八个位置，反之亦然。实际上，除了此约束外，SKINNY的设计者还施加了另外两个约束：（1） PT必须构成单一轮换；（2）它将前8个元素映射到后8个位置。在我们的搜索中，将放宽这两个约束。这使得搜索空间从略小于8!种可能的 PT选择扩大到(8!)2。因此，我们将操作在一个无法通过暴力破解覆盖的空间中，该空间包含可能导致具有更高安全裕度密码算法的候选置换。然而，由于我们放宽了约束（2），这些置换在某些环境中的实现开销可能会更高。因此，我们对 PT的搜索应被视为在可能更高的安全性与较低速度之间的一种权衡。

在应用元启发式算法之前，让我们先澄清几点。首先，SKINNY有多个版本，我们将重点关注SKINNY-64-192，即具有三个tweakey（n= 64, t= 3n= 192）的64位版本，也就是对攻击者而言自由度最高的轻量级版本。其他版本可类似处理：从64位过渡到128位将需要更强的计算能力7,，而将tweakey字的数量从三个减少到两个或一个则需要更少的计算能力8。其次，最优特征不一定必须在整个密码算法上找到；实际上，一旦在轮数减少的特征中活跃S盒的数量达到某个阈值，该密码算法就被认为是安全的。在SKINNY-64-192中，该数值9为33，根据[4],原始选择的PT参数，经过18轮后达到此值。我们的目标是在更早的16轮内实现33个活跃S盒10。因此，我们的目标函数 f（PT）定义为16轮中最优特征中的活跃S盒数量。

让我们澄清上述几点。首先注意，SKINNY的原始置换 P o T定义为

P o T=(0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 9 15 8 13 10 14 12 11 0 1 2 3 4 5 6 7) (1) 7 SKINNY的128位版本使用SKINNY采用8位S盒，其最大差分传播概率与64位版本中使用的4位S盒的 2 −2相同。因此，为了实现128位安全性（而非64位安全性），最优特征中的活跃S盒数量必须大得多，这反过来导致搜索复杂度更高。 8有关这些版本的结果，请参见附录 A。

9该数值由状态大小和S盒的最佳差分转移概率决定。SKINNY的状态为64比特，4位S盒中差分转移的最高概率为 2 −2，因此如果活跃S盒的数量为1+ 64 2 = 33，则该密码算法能够抵抗相关密钥变体差分攻击。 10无法先验预测轮数。我们重点关注16轮，但如果未能成功，我们总可以比较在16轮中达到的活跃S盒数量，或者在17轮中是否达到了33个活跃S盒。

根据设计者所述，并通过我们自己的ILP工具验证， f(PT o) = 27。我们正在寻找另一个置换 PT

PT=( 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 a0 a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15) ,

使得 f(PT) 尽可能大。注意，有一个额外的条件，要求 ai ≥ 8 对于 i= 0，1，…，7 成立，且 ai< 8 对于 i= 8，9，…，15 成立，以确保前8 个元素被发送到后8 个位置，反之亦然。

让我们关注模拟退火。为了用这种元启发式算法解决优化问题，我们首先需要确定三个参数： ε(PT) α(T) T0。作为邻域函数 ε(PT)，我们使用随机换位，即在 PT中随机选择两个索引，并交换对应元素的值。但需要注意的是，索引的选择不能完全随机，因为 ε(PT)必须满足附加条件。因此，为了正确实现ε(PT)，我们首先选择 PT中的半部分以确定换位发生的区域，然后再从同一半部分中随机选择两个元素。对于冷却方案α(T)，如前所述，我们采用逆向冷却 α(T) = T [1, 2]范围内的值。我们的终止条件是基于时间的，即在8核处理器上运行元启发式算法约一天后停止搜索，并输出找到的最佳解。

此外，让我们重点关注遗传算法及其所使用的参数。在我们的所有实现中，种群大小为50。为了测试不同选择函数的有效性和影响，我们使用了全部四种选择函数。此外，我们采用0.01的变异率，以及一种与模拟退火中的 ε(PT)非常相似的变异函数（即变异由一次随机换位组成）。最后，我们使用20%比率的精英策略。终止条件与模拟退火类似，但我们允许更长的时间。

两种元启发式算法的优化结果如下。模拟退火和遗传算法均能够找到满足 PT的 f(PT)= 33的置换。模拟退火在不同参数 β和 T0选择下的表现相似，即我们未发现任何显著差异。平均而言，它需要约1000次目标函数 f(x) 调用以找到满足 PT的f(PT)= 33的置换。另一方面，遗传算法在某些选择函数下的表现更优。在三次试验的平均情况下，为找到满足 PT的f(PT)= 33，使用随机选择需要950次调用，使用排名选择需要1380次调用，使用轮盘赌选择需要2250次调用，而使用锦标赛选择则需要5900次调用。因此，我们可以得出结论： 模拟退火以及采用随机或排名选择的遗传算法表现相似。

这个数字（1380）不一定必须能被种群大小（50）整除。原因有两个：（1）一旦找到足够好的构造，我们就停止搜索，而不更新整个种群；（2）我们使用精英策略，这意味着在每一代中仅更新 50 ·(1 − elitism)个个体。

表1。 使用模拟退火（第二行）和遗传算法（第三行）找到的置换 PT 示例，以及在 SKINNY‐64‐192中使用时针对相关密钥tweakey攻击所达到的安全级别。第二列是置换的具体参数，第三列是其安全性，即根据轮数在减少轮次的特性中活跃S盒的数量。高亮的数字表示已达到相关tweakey安全阈值的最低活跃S盒数量。

方法	PT	14 15 16 17 18
原始	9 15 8 13 10 14 12 11 0 1 2 3 4 5 6 7	19 24 27 31 35
遗传算法	模拟退火 11 9 14 8 12 10 15 13 2 0 3 6 7 5 1 4 24 28 33 36 39	14 11 8 9 15 13 10 12 1 2 0 7 5 4 3 6 24 28 33 36 39

在表1中展示了使用模拟退火和遗传算法找到的置换 P SA T, P GA T的示例，满足 f(P SA T)= f(P GA T)= 33。在性能测量方面，表中还给出了最优特征在14到 18轮范围内的活跃S盒数量，而不仅限于16轮。显然，这两个新置换相比 SKINNY的原始置换，产生了更多的活跃S盒。

在本小节的最后，我们讨论元启发式算法在SKINNY中的进一步应用。一个潜在的方向是针对 PT和轮调制密钥相加，优化对相关密钥扩展攻击的抵抗能力，即通过改变置换 PT，并确定tweakey字中的哪8个半字节应与状态进行异或（而非前两行的8个半字节）。

3.2 基于AES轮的构造 [23]

基于AES轮函数的软件优化设计在[23]中提出。本文作者的主要目标是提供在最新的英特尔处理器上高效的对称密钥构造（作为消息认证码和认证加密方案的构建模块）12。作者展示了七种构造，在英特尔处理器Ivy Bridge、 Haswell和Skylake上每字节仅需零点几个周期即可运行。

所提出的构造具有由 s个128位字组成的状态。该状态通过图2中给出的轮函数进行变换，其中 A表示一轮高级加密标准。此外 A，唯一剩下的操作是消息字Mi j 与状态字 Xi j之间的异或。每种构造都具有一个称为速率的参数 ρ，其定义为处理一个128位消息字所需的高级加密标准轮数。也就是说， ρ是调用 A的次数与（一轮中）不同消息字数量的比值。速率越低，12这些处理器具有称为AES‐NI的特殊指令集，可以将高级加密标准轮函数作为单条指令执行。

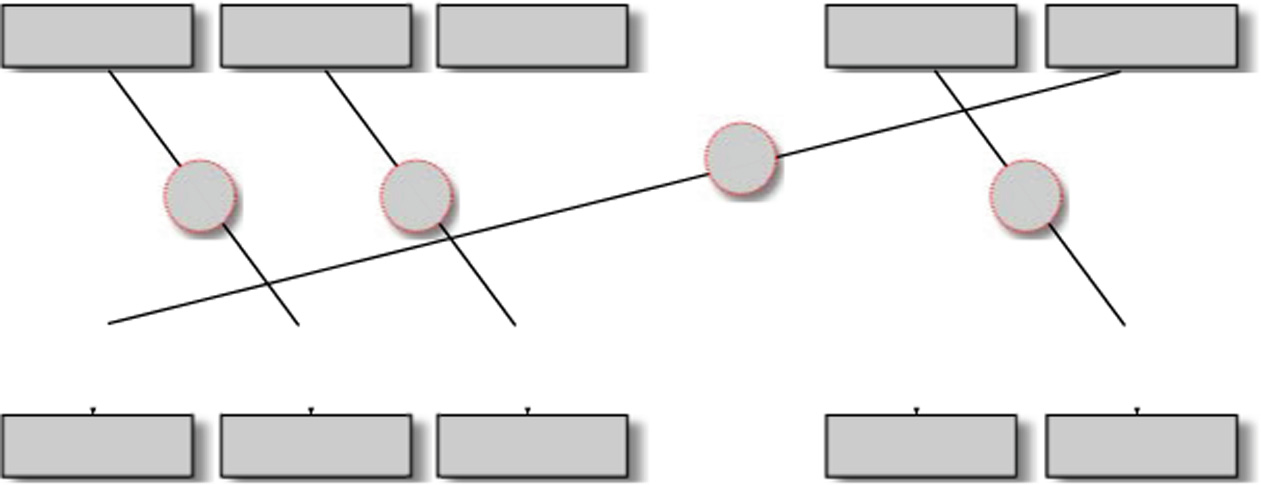
更快的设计，因此作者的目标是尽可能降低速率。

如果一种结构不存在所谓的内部碰撞，则认为其是安全的，内部碰撞是一种特殊类型的差分特征：它们在状态13中的差值以零开始并以零结束。该结构应提供128位安全性，即导致内部碰撞的差分特征的概率不得超过 2−128。为了找到最优特征及其概率，作者将问题归结为计算活跃S盒的数量，并使用前述整数线性规划工具来获得此数量的下界。128位的安全级别对应于最优特征中至少包含22个活跃S盒14。

所提出的七种构造具有不同数量的状态字（7 到 12）和不同的速率（范围在 [2, 3]内）。对于特定的状态大小和速率选择，作者使用某种启发式方法（论文中未作说明）来搜索图2中定义的所有构造的空间，并仅考虑那些能够抵抗内部碰撞的构造，即其最优特征至少包含 22 个激活S盒。具有最低内部碰撞概率（即最多激活S盒数量）的构造被视为最佳构造。

接下来，我们使用元启发式算法根据[23]的设计准则来优化构造。优化问题很明确：对于特定的状态大小 s和速率 ρ，寻找一个如图2 所示的轮函数，使其定义的构造中导致内部碰撞的最佳差分特征具有最多的活跃S盒数量。再次说明，目标函数 f的作用由整数线性规划承担，该规划返回活跃S盒数量的下界。

为了理解目标函数的输入内容，让我们关注图2。注意，轮函数中有三种红色（可选）变换。首先，对 s的每次调用都是可选的。因此，我们可以使用 s比特向量 aes masks来描述对 A调用的特定配置，其中 i的第 aes masks位被置为1当且仅当在轮函数中 A被13差分通过消息字引入，随后又被抵消。14由于高级加密标准中S盒的差分传播概率为 2 − 6，因此128位安全意味着 128 6 +1= 22个活跃S盒。

应用于 Xi。其次，所有 s个字的前馈（红色竖线）也可以用一个 s比特向量 feed masks来描述。最后，消息字的异或 Mij可以用一个包含 s个坐标的向量 messages来表示，每个坐标是范围在[0, w]内的整数值，其中 w是一轮中消息字的总数。值为0表示没有消息字进行异或，而任何正值对应于被异或的消息字的索引。因此，每种可能的构造都可以用三个向量来描述：aes masks、 feed masks和 messages。但需要注意，并非所有组合都是可能的，因为 aes masks和 messages的取值不能任意，它们必须与速率 ρ一致。例如，如果 ρ= 2且 aes masks的汉明重量为6，则向量 messages只能包含值1、2和3，并且这些值每一个至少出现一次，以确保构造的速率为2。进一步假设三元组(aes masks, feed masks, messages)符合预定义的速率 ρ。那么，对于固定状态大小 s和速率 ρ，我们的优化问题可以定义为：

max
aes masks,feed masks,messages
f(aes masks, feed masks, messages)

我们优化了 [23]中提出的七种构造中的六种。我们省略了一种，其速率为 ρ= 2，尺寸 为 s= 12，因为它的目标函数计算成本过高——在一次输入上计算它花费了我们半天时间 f。

为了解决优化问题，我们使用模拟退火和遗传算法，并设置如下参数。在模拟退火中，邻域函数 ε(x)包括在三个向量aes masks, feed masks, messages中的某些（或全部）向量上翻转1–2位（并额外对速率 ρ进行检查）。此外，我们采用逆向冷却 α(T)，其中 β= 0.003，初始温度为T0= 1.5。在遗传算法中，种群大小为30，结合随机选择函数、均匀交叉、变异率为0.01、基于随机翻转位的变异函数以及20%的精英策略。两种元启发式算法的终止准则均基于目标函数调用次数，分别为500次调用（针对较小的搜索空间）或700次调用（针对较大的搜索空间）。

元启发式算法的输出结果如表4所示。对于所有六种构造，两种元启发式算法均能找到更优的候选方案，与原始提案相比，活跃S盒的数量增加了13%– 44%。模拟退火的表现略优于遗传算法——在目标函数调用次数有限的情况下，它找到了具有更高安全裕度的构造。我们怀疑这是由于终止准则所致，因为遗传算法需要更多代才能找到更优解（见表2）。

最后，我们注意到，我们还运行了元启发式算法，以寻找在安全性更高且效率更优方面能够与已发表构造相竞争的新构造[23]不仅在安全性方面，而且在效率方面也是如此。有关更多详细信息，请参阅附录C。

表2. 基于AES轮的构造。SA和GA分别代表模拟退火和遗传算法。

| | 方法 状态大小 速率 aes | mask feed mask messages | 活跃S盒 |
| — | — | — |
| [23]
GA
SA | 6 3
6 3
6 3 | 111111 100100 011022
111111 100100 122020
111111 011100 102110 | 22
26
27 |
| [23]
GA
SA | 7 3
7 3
7 3 | 1111110 1101101 1012020
0111111 0100110 0101201
1110111 1111100 0100211 | 25
35
36 |
| [23]
GA
SA | 7 2.5
7 2.5
7 2.5 | 1101110 0100001 1111222
1111001 0010110 1201102
1011110 0110100 1021102 | 22
25
26 |
| [23]
GA
SA | 8 3
8 3
8 3 | 11101110 11011101 10102020
11110011 00110000 10102022
00111111 01001000 20221220 | 34
42
45 |
| [23]
SA
GA | 8 2.5
8 2.5
8 2.5 | 11011100 01000011 11112222
10011011 10000110 02012021
11111000 01100100 11022102 | 23
30
30 |
| [23]
GA
SA | 9 3
9 3
9 3 | 111111111 100100100 011022033 25
111111111 111101111 012133031 34 111111111 100100111 010321121 34 |

4 结论

元启发式算法是广泛用于求解优化问题的算法。对称密钥原语的设计可以被视为此类问题之一，因此可以使用元启发式算法来寻找更优的设计方案。因此，元启发式算法可作为对称密钥原语自动设计的工具。与暴力破解和随机搜索不同，元启发式算法是非平凡的工具，在缺乏更优的启发式方法或其他更先进的搜索方法时，应对其进行仔细审查。

我们使用了两种元启发式算法——模拟退火和遗传算法，以安全性为目标优化设计。我们选择这些元启发式算法是基于它们的流行程度和已报道的成功案例——两者都被认为在知名问题上表现最佳。另一方面，我们选择安全性作为优化参数，因为这导致了定义明确且可计算的目标函数15。我们用C语言实现了这两种元启发式算法——编码过程相当直接。我们花费了数千CPU小时来测试良好的参数集，并为SKINNY和AES轮结构中的设计优化问题寻找近似解。结果是积极的——元启发式算法能够为这两种对称密钥原语找到更优的组件，有时使被优化组件的性能提升超过40%。因此我们可以得出结论：元启发式算法可以作为对称密钥原语自动设计的有效工具。

未来研究可能侧重于扩展应用领域和元启发式算法的多样性。这包括将其他设计问题表述为优化问题，并随后使用所提出的元启发式算法来求解这些问题。我们强调，这些优化问题不一定必须与安全性的提升相关，也可以以更高的吞吐量、更小的尺寸等为目标。此外，使用模拟退火和遗传算法之外的其他元启发式算法，也可能改进密码原语的设计方法。一些更先进的元启发式算法，例如多目标遗传算法NSGA‐II [13],在解决与多维优化（即基于多个准则的优化）相关的设计问题方面可能表现优异。