带力感知反馈的手术钻

一种用于机器人辅助耳科手术的新型带有力感知和力反馈功能的手术钻孔器械

1. 引言

在许多外科领域（如骨科手术、耳科手术、颌面外科手术和神经外科手术）中都需要进行骨钻孔[1]。通过在颞骨内进行钻孔，可以到达中耳、内耳和颅底的重要解剖结构，从而实施常见的耳科手术操作，包括听神经瘤切除术、乳突切除术和人工耳蜗植入术，这些手术均要求高精确度和精度。因此，在这些手术过程中必须考虑周围解剖结构及钻孔深度。否则，可能会损伤骨骼周围邻近的静脉、动脉、神经、脑组织、脊髓等结构，从而对患者造成永久性伤害[2]。目前，骨钻孔主要使用手持式电动或气动钻孔工具完成。外科医生通过脚踏板或按钮控制钻头速度，并手动施加力于骨骼以去除骨质。

这些手持钻孔工具的一个主要缺点是，外科医生通常无法可靠地判断何时已去除适当的材料量或达到目标深度。由于钻削力的惯性，在发生穿透时，钻头可能会沿钻孔轴线被无意中进一步推进。此外，外科医生的手部生理性震颤也可能导致精度降低。因此，钻孔过程主要依赖于外科医生的经验与直觉。

为了解决这些问题，一些研究人员已探讨了改进外科钻孔技术的方法。一些方法专注于深度控制和穿透检测方案，并已被提出[3–11]。为了获得更高的精确度和精度，已开发出不同尺寸、复杂性和成本的机器人装置与系统。微型工作台被提出，用于利用附着于患者颅骨中植入的骨锚钉的微立体定向架，精确引导钻头沿期望的直线轨迹运动[12–15]。一种安装在刚性预定位框架上的附着于骨的并联运动学机构被开发出来，以精确引导轨迹[16]。还研究了一种作为工具导向器的微立体定向架，可通过机器人进行调节[17]。提出了一种用作微创人工耳蜗植入术中钻头导向器的被动式Stewart‐Gough平台。该机构可与植入患者颅骨中的球形头部骨锚钉耦合[18, 19]。开发了一种名为DRIBON的新型机电一体化骨钻工具，可自动执行骨钻过程，并在发生穿透或层间过渡时高效停止[20]。开发了一种自动钻导系统，可适配现有微创人工耳蜗植入手术系统，并提供一种测量面神经处温度升高的方法[21]。

一种用于侧颅底手术的机器人系统基于台式机械臂和力/扭矩（F/T）传感器开发，该系统集成了光学跟踪系统、影像引导系统、头固定系统和触摸屏界面[22], 。结果表明该系统具有应用前景，但其性能依赖于跟踪系统以及与患者监测和机器人对准相关的误差。为消除这一局限性，研究人员开发了一种紧凑型、骨骼附着式、计算机断层扫描（CT）影像引导的机器人，用于颞骨铣削，该机器人通过预定位框架上的三个钛球固定在患者身上[23]。模型实验结果表明，该系统具有高精度，且实验切除体积与关键结构之间无重叠。在尸体模型中，使用配备红外跟踪系统和骨植入标记的三菱RV‐3S工业机器人实现了人工耳蜗植入的自主经皮植入[24]。结果表明，该系统准确可靠，但其性能依赖于配准的精度水平。开发了一种远程机器人系统，包括Phantom Omni（SensAble Technologies, Inc.）主控机器人和缆索传动机构从动机器人[25]。该原型在人颞骨标本中进行了测试，结果显示耳科医生可在速度/位置和位置/位置控制模式下成功将活塞假体植入镫骨切开术部位。采用一种四自由度（DOF）紧凑型骨附着机器人执行手术中的乳突切除术部分。目标切除体积可由外科医生在术前通过CT扫描手动识别，并转换为机器人的铣削路径[26]。对手持式操作器进行了全面综述，并在[27]中提出了手持式医疗机器人领域的新兴技术趋势以及促进其更广泛临床应用的未来发展方向。

一项使用达芬奇系统进行人工耳蜗植入术的尸体可行性研究已开展[28]。研究人员开发了一种附件，可将动力钻连接至机械臂之一，并通过颞骨锥束高分辨率CT扫描的分割技术，在外科医生的视野中集成了增强现实功能。手术在两具颞骨上成功完成。然而，研究也报告了三项局限性：首先，由于手术中现有设备（如吸力冲洗器）体积过大，因此需要一种更小轮廓的可调式吸力冲洗装置，以便在面隐窝中进行导航；其次，需提高3D内窥镜的放大倍数，以改善经后方鼓室造口的视野可视化效果；第三，为了充分评估该系统的精度、精确度和可行性，还需采用此方法完成更多尸体标本的手术。此外，该系统尚无力反馈功能。

与手持器械或机器人相比，主从机器人或协作机器人可能实现更高的精度和精确度。像达芬奇手术系统这样的主从式手术机器人系统具有3D手术视觉、运动缩放、精细运动、手眼协调和手部震颤抑制等优势，近年来取得了显著发展，并已应用于泌尿外科手术、普通腹腔镜手术、妇科腹腔镜手术和心脏手术等多种手术中[29,30]。

本文基于直觉外科公司（美国加利福尼亚州森尼韦尔）捐赠的达芬奇研究套件（dVRK）开展研究，旨在探讨使用具备力感知和力反馈功能的主从式手术机器人系统完成耳科手术中外科钻孔的可行性。

2. 手术钻孔器械的设计

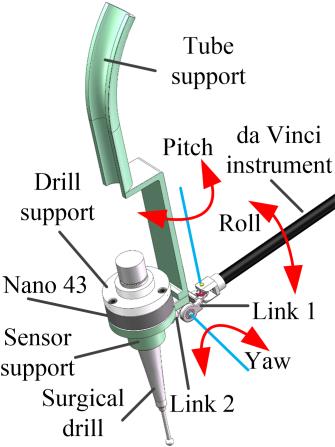
为了适配患者侧操作臂（PSM）的无菌适配器，采用了一种3自由度肌腱驱动手术钻具，基于达芬奇手术器械设计，集成了ATI工业自动化公司（美国北卡罗来纳州阿普莱克斯）生产的Nano43力/扭矩传感器和林瓦特克公司（美国纽约州奥尔巴尼）生产的Hall Osteon钻，如图1所示。该手术钻孔器械除手术钻轴线的自滚动运动外，可提供包括俯仰、偏航和滚动自由度在内的三自由度运动，以及力和扭矩感知能力。

该器械的这些自由度由肌腱‐滑轮系统和直流伺服电机驱动。滚动运动、俯仰运动和偏航运动的范围均为‐90°至90°。

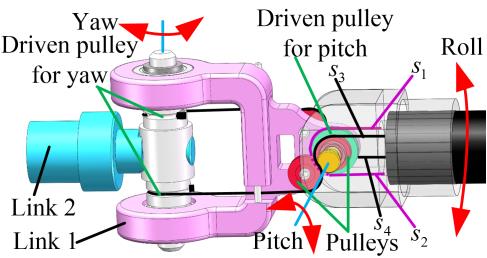
肌腱传动的布局设计如图2所示。滚动自由度可由改进型达芬奇手术器械提供。连杆1与俯仰从动滑轮、连杆2与偏航从动滑轮分别配合连接。肌腱 s₁ 和 s₂ 可驱动俯仰从动滑轮绕俯仰轴旋转，从而实现俯仰自由度。肌腱 s₃ 和 s₄ 可驱动偏航从动滑轮绕偏航轴旋转，从而实现偏航自由度。

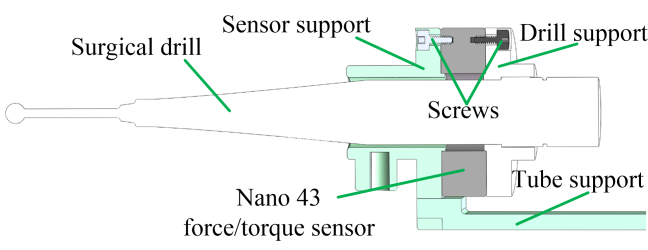
手术钻与力/扭矩传感器的接口设计如图3所示。力/扭矩传感器的传感器支架与安装适配板通过三个螺钉连接。钻头支架与力/扭矩传感器的工具适配板通过三个螺钉连接。钻头与钻头支架通过紧定螺钉连接。管夹支架与传感器支架配合安装。管夹支架用于固定Hall Osteon钻的软管和电线，以及力/扭矩传感器的电缆，可确保力/扭矩传感器的测量值不受其影响。

3. PSM1的正向运动学与耦合矩阵

为了实现主从式直观运动控制、手术钻孔器械的解耦控制以及力/力矩（F/T）信息变换，对dVRK系统的PSM1的Denavit‐Hartenberg（DH）参数、运动学、刀尖偏移变换矩阵和耦合矩阵进行了分析并提供。

3.1 正向运动学

根据改进的DH约定，为PSM1的每个连杆分配了坐标系。图4显示了PSM1的坐标系分配以及我们的手术钻孔器械。

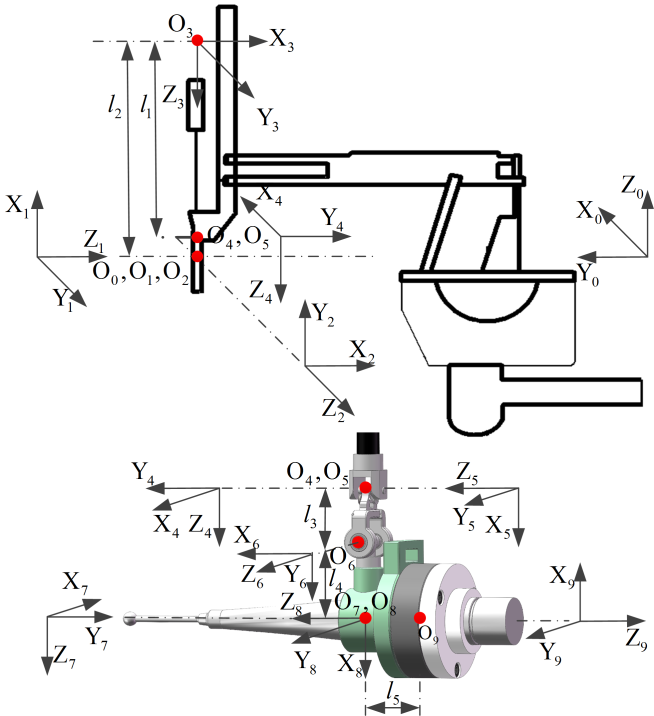
原点 O₀ 以及坐标系0、1和2的原点位于远程运动中心（RCM），坐标系4和5的原点，以及坐标系7和8的原点分别重合。坐标系8被分配给手术钻孔器械的控制点。Nano43力/扭矩传感器的坐标系是坐标系9。PSM1的改进DH参数见表1。

表1 PSM1的改进DH参数

第i帧	αᵢ₋₁	aᵢ₋₁	dᵢ	θᵢ
1	π/2	0	0	θ₁ + π/2
2	-π/2	0	0	θ₂ - π/2
3	π/2	0	d₃ - 2l₂	0
4	0	0	l₁	θ₄ - π/2
5	-π/2	0	0	θ₅ - π/2
6	-π/2	l₃	0	θ₆ - π/2
7	-π/2	0	l₄	π/2
8	π/2	0	0	π/2
9	π	0	l₅	π

其中 θᵢ (i=1, 2, 4, 5, 6) 和 d₃ 是相应的关节变量。

配备手术钻孔器械的PSM1的正向运动学可通过以下方式获得：

$$
^0_8T = ^0_1T \cdot ^1_2T \cdot ^2_3T \cdot ^3_4T \cdot ^4_5T \cdot ^5_6T \cdot ^6_7T \cdot ^7_8T
$$

其中 $^i_jT$ 是一个将第i帧与第j帧关联起来的变换。

刀尖偏移变换矩阵可通过以下方式获得：

$$
^4_6T =
\begin{bmatrix}
1 & 0 & 0 & 0 \
0 & 1 & 0 & 0 \
0 & 0 & 1 & l_6 \
0 & 0 & 0 & 1
\end{bmatrix}
$$

3.2 耦合矩阵

三自由度肌腱驱动手术钻具的传动原理图如图5所示，其中 rᵢ (i=1,2,6) 和 r_diskᵢ (i=1,2,3) 分别为滑轮和圆盘的半径；θᵢ (i=4,5,6) 和 θ_diskᵢ (i=1,2,3) 分别为关节角位移和从动圆盘角位移。

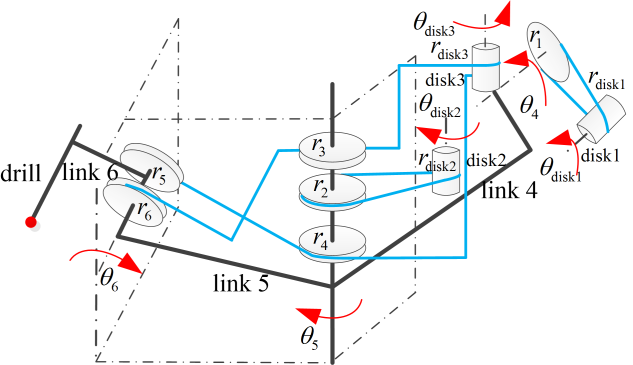
根据肌腱运动位移相等性，关节角位移 θ_joint 和从动圆盘角位移 θ_disk 之间的关系可以描述为：

$$
A \theta_{joint} = R_{disk} \theta_{disk}
$$

其中

$$
A =
\begin{bmatrix}
r_1 & 0 & 0 \
0 & r_2 & 0 \
0 & 0 & r_6
\end{bmatrix}
,
\quad
\theta_{joint} =
\begin{bmatrix}
\theta_4 \
\theta_5 \
\theta_6
\end{bmatrix}
,
\quad
R_{disk} =
\begin{bmatrix}
r_{disk1} & 0 & 0 \
0 & r_{disk2} & 0 \
0 & 0 & r_{disk3}
\end{bmatrix}
,
\quad
\theta_{disk} =
\begin{bmatrix}
\theta_{disk1} \
\theta_{disk2} \
\theta_{disk3}
\end{bmatrix}
$$

利用公式(3)并考虑旋转关节上的功，可得到从关节到盘以及从盘到关节的位置耦合矩阵，以及从盘到关节和从关节到盘的扭矩耦合矩阵：

$$
M_{j2dp} = M_{d2jp}^\mathrm{T} =
\begin{bmatrix}
\frac{r_1}{r_{disk1}} & 0 & 0 \
0 & \frac{r_2}{r_{disk2}} & 0 \
0 & 0 & \frac{r_6}{r_{disk3}}
\end{bmatrix}
,
\quad
M_{j2dt} = M_{d2jt}^\mathrm{T} =
\begin{bmatrix}
\frac{r_{disk1}}{r_1} & 0 & 0 \
0 & \frac{r_{disk2}}{r_2} & 0 \
0 & 0 & \frac{r_{disk3}}{r_6}
\end{bmatrix}
$$

4. 主从运动与力反馈控制

基于dVRK的主从式手术钻机器人系统如图6所示，包括第一代达芬奇外科手术机器人系统、由约翰斯·霍普金斯大学和伍斯特理工学院开发的控制系统[31,32],以及设计的手术钻孔器械。

当前的主从运动和力反馈控制结构如图7所示。由人工操作者操控的右侧主工具操作器(MTMR)通过运动学计算出的位置（旋转/平移）经过映射变换和位置缩放因子后发送给PSM1。安装在PSM1的外科钻孔器械上的Nano43力/扭矩传感器测得的环境力通过力和力矩变换以及力缩放因子反馈至MTMR。力反馈可通过通过使用环境力和MTMR的雅可比矩阵的转置获得的关节力矩。患者侧机械臂1每个关节使用本地PID控制器以确保位置/速度跟踪。

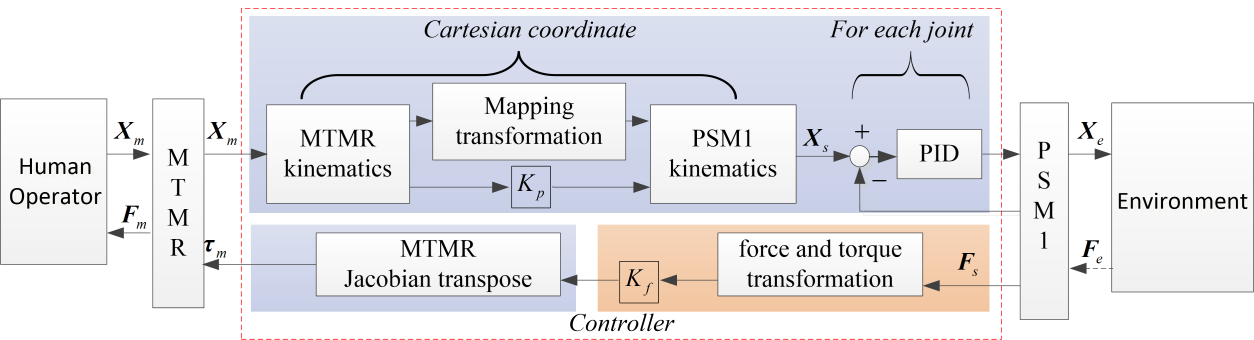
4.1 主从运动控制

运动缩放可使MTMR的大幅度运动对应PSM1的小幅度运动，即使在MTMR出现抖动操作时也能保持PSM1的稳定。为实现直观运动控制，显示器上显示的PSM1控制点运动方向必须与外科医生操作的MTMR运动方向一致。

所需的旋转矩阵可以表示为：

$$
R_{ECM}^{tcp} = R_{base}^{ECM} \cdot R_{world}^{base} \cdot R_{monitor}^{world} \cdot R_{MTMR}^{monitor} \cdot R_{base}^{MTMR} \cdot R_{PSM1}^{base}
$$

其中，$R_{base}^{MTMR}$、$R_{base}^{PSM1}$、$R_{base}^{ECM}$、$R_{monitor}$ 和 $R_{world}$ 分别是MTMR的基坐标系、PSM1的基坐标系、内窥镜相机操纵器（ECM）的基坐标系、显示器坐标系、ECM的控制点坐标系以及世界坐标系。

由公式(5)可以看出，旋转矩阵仅在ECM移动时发生变化，因为$R_{base}^{PSM1}$和$R_{base}^{MTMR}$位于固定坐标系之间。当仅考虑主端和从端基座坐标系时，旋转矩阵可计算为：

$$
R_{base}^{PSM1} \cdot R_{MTMR}^{base} =
\begin{bmatrix}
-1 & 0 & 0 \
0 & -1 & 0 \
0 & 0 & 1
\end{bmatrix}
$$

MTMR的位置和姿态被转换到PSM1的基坐标系中，可以描述为：

$$
\begin{bmatrix}
^{\text{base}} {\text{PSM1}}T {\text{tcp}} \
1
\end{bmatrix}
=
\begin{bmatrix}
R_{\text{PSM1}}^{\text{base}} & 0 \
0 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
R_{\text{MTMR}}^{\text{base}} & 0 \
0 & 1
\end{bmatrix}^\mathrm{T}
\cdot
\begin{bmatrix}
^{\text{base}} {\text{MTMR}}T {\text{tcp}} \
1
\end{bmatrix}
=
\begin{bmatrix}
R_{\text{PSM1}}^{\text{base}} \cdot R_{\text{MTMR}}^{\text{base}} & 0 \
0 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
\Delta x \
\Delta y \
\Delta z \
1
\end{bmatrix}
\cdot K_p
$$

PSM1在其基坐标系中的期望工具控制点可以描述为：

$$
^{\text{base}} {\text{PSM1}}T {\text{tcp(desired)}} = g(T_{\text{PSM1}}^{i-1}, T_{\text{MTMR}}^i, \text{couple}(i))
$$

其中$g(\cdot)$是函数，以及耦合标志(i)。耦合标志(i)是一个布尔标志，用于指示MTMR和PSM1是否耦合。如果MTMR和PSM1耦合，则couple(i)=True；否则，couple(i)=False。$T_{\text{PSM1}}^{i-1}$和$T_{\text{MTMR}}^i$分别是第i–1个和第i个时间步。

当PSM1与MTMR耦合时，PSM1将根据位置缩放因子跟随MTMR的运动。PSM1的期望工具控制点被发送到PSM1的逆运动学模块，并转换为相应的关节角度。

4.2 力/扭矩变换

安装在手术钻孔器械上的Nano43力/扭矩传感器不仅测量环境施加在手术钻上的接触力和扭矩，还测量由重力的、惯性效应以及线性偏差引起的非接触力。因此，力/扭矩传感器测得的力和扭矩可计算为：

$$
\begin{bmatrix}
F_S \
\tau_S
\end{bmatrix}
=
\begin{bmatrix}
F_E \
\tau_E
\end{bmatrix}
+
\begin{bmatrix}
F_G \
\tau_G
\end{bmatrix}
+
\begin{bmatrix}
F_I \
\tau_I
\end{bmatrix}
+
\begin{bmatrix}
F_O \
\tau_O
\end{bmatrix}
$$

其中，$F_S$和$\tau_S$是力/扭矩传感器测得的力和扭矩；$F_E$和$\tau_E$是环境施加在手术钻上的力和扭矩；$F_G$和$\tau_G$是重力引起的力和扭矩；$F_I$和$\tau_I$是手术钻动力学产生的惯性力和扭矩；$F_O$和$\tau_O$是线性力和扭矩偏移。

需要将接触力和扭矩与力/扭矩传感器的测量值区分开，并消除非接触力和扭矩的影响。由于装有手术钻孔器械的PSM1以非常低的速度操作，此处忽略手术钻的动力学效应。当手术钻在PSM1的工作空间内自由移动时，公式(9)可表示为：

$$
\begin{bmatrix}
F_S \
\tau_S
\end{bmatrix}
=
\begin{bmatrix}
F_G \
\tau_G
\end{bmatrix}
+
\begin{bmatrix}
F_O \
\tau_O
\end{bmatrix}
$$

影响力/扭矩传感器测量的力可以计算为

$$
F_G = m \cdot g_s = m \cdot R_s^0(q) \cdot g_0
$$

其中，g是重力矢量；m是手术钻的质量；g₀是在PSM1的坐标系0中描述的重力加速度矢量；g_s是在力/扭矩传感器坐标系中描述的重力矢量，$R_s^0$是力/扭矩传感器在PSM1的坐标系0中的旋转矩阵。

类似地，作用在力/扭矩传感器上的扭矩可以通过以下方式计算

$$
\tau_G = r_{sd} \times F_G = r_{sd} \times m \cdot R_s^0(q) \cdot g
$$

其中$\tau_G$是重力扭矩向量，$r_{sd}$是从力/扭矩传感器原点到手术钻质心的向量。

结合公式(10)、公式(11)和公式(12)可得：

$$
\begin{bmatrix}
F_{Sx} - F_{Ox} \
F_{Sy} - F_{Oy} \
F_{Sz} - F_{Oz} \
\tau_{Sx} - \tau_{Ox} \
\tau_{Sy} - \tau_{Oy} \
\tau_{Sz} - \tau_{Oz}
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & 0 & -r_z g_y & r_y g_z \
0 & 1 & 0 & -r_z g_x & r_x g_z \
0 & 0 & 1 & r_y g_x & -r_x g_y \
0 & 0 & 0 & 1 & 0 \
0 & 0 & 0 & 0 & 1 \
0 & 0 & 0 & 0 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
F_{Ex} \
F_{Ey} \
F_{Ez} \
m
\end{bmatrix}
$$

公式(13)包括10个未知参数：力和扭矩的偏移值、质心位置以及质量手术钻。根据公式(13)，可得到以下公式(14)和公式(15)：

$$
F_s = Y_F \cdot X_F
$$

其中

$$
Y_F =
\begin{bmatrix}
1 & 0 & 0 & -r_z g_y \
0 & 1 & 0 & -r_z g_x \
0 & 0 & 1 & r_y g_x
\end{bmatrix}
,
\quad
X_F =
\begin{bmatrix}
F_{Ox} \
F_{Oy} \
F_{Oz} \
m
\end{bmatrix}
$$

$$
\tau_s = Y_\tau \cdot X_\tau
$$

其中

$$
Y_\tau =
\begin{bmatrix}
1 & 0 & 0 & 0 & -r_z m g_y & r_y m g_z \
0 & 1 & 0 & -r_z m g_x & 0 & r_x m g_z \
0 & 0 & 1 & r_y m g_x & -r_x m g_y & 0
\end{bmatrix}
,
\quad
X_\tau =
\begin{bmatrix}
\tau_{Ox} \
\tau_{Oy} \
\tau_{Oz} \
r_x \
r_y \
r_z
\end{bmatrix}
$$

根据公式(9)，环境施加在手术钻孔器械上的力和扭矩可以

$$
\begin{bmatrix}
F_E \
\tau_E
\end{bmatrix}
=
\begin{bmatrix}
F_S \
\tau_S
\end{bmatrix}
-
\begin{bmatrix}
F_G \
\tau_G
\end{bmatrix}
-
\begin{bmatrix}
F_O \
\tau_O
\end{bmatrix}
$$

作用在坐标系8中手术钻上的力和扭矩可以描述为:

$$
\begin{bmatrix}
\hat{F} E^8 \
\hat{\tau}_E^8
\end{bmatrix}
=
\begin{bmatrix}
R_9^8 & 0 \
-p {98} \times R_9^8 & R_9^8
\end{bmatrix}
\cdot
\begin{bmatrix}
F_E^9 \
\tau_E^9
\end{bmatrix}
$$

其中

$$
R_9^8 =
\begin{bmatrix}
-1 & 0 & 0 \
0 & 1 & 0 \
0 & 0 & -1
\end{bmatrix}
,
\quad
\hat{p} {98} =
\begin{bmatrix}
0 & 0 & l_5 \
0 & 0 & -l_5 \
0 & 0 & 0
\end{bmatrix}
,
\quad
p {98} =
\begin{bmatrix}
0 \
0 \
-l_5
\end{bmatrix}
$$

4.3 钻削力反馈的实现

PSM1的工具控制点的力矩被反馈到MTMR，MTMR在MTMR的工具控制点产生相同大小的力，以实现力反馈。

使用从PSM1的控制点到MTMR的控制点的力矩变换

体坐标系下的广义力可以表示为：

$$
w_{\text{tcpPSM1}} =
\begin{bmatrix}
R_{\text{MTMR}}^{\text{tcp}} & 0 \
0 & R_{\text{MTMR}}^{\text{tcp}}
\end{bmatrix}
\cdot
w_{\text{tcpMTMR}}
$$

给定关节力矩，可通过MTMR的工具控制点获得期望的体坐标系下的广义力

$$
w_{\text{tcpMTMR}} = (J_b)^\dagger \cdot \tau
$$

其中$(J_b)^\dagger$是MTMR的体雅可比转置矩阵的广义逆矩阵。

5. 实验与结果

完成了几项实验，以验证使用新开发的工具与达芬奇机器人系统的可行性。

5.1 轨迹跟踪实验

为了验证PSM1运动学的有效性，在命令模式下进行了轨迹跟踪实验。通过Certus HD光学跟踪系统（北方数字公司，加拿大安大略省滑铁卢）测量了PSM1在笛卡尔空间中的实际轨迹。使用六个有源标记构建一个刚体，该刚体固定在机器人基座上。另一个有源标记安装在工具尖端。通过使用刚性框架并定义新的坐标系，可以测量工具尖端相对于机器人基座的运动。期望的指令轨迹被设计并描述为：

$$
\begin{cases}
X = 25 \cos(n) \
Y = 25 \sin(n) \
Z = 2
\end{cases}
, \quad n \in [0,4\pi]
$$

为了验证主从运动控制的正确性，在主从模式下进行了轨迹跟踪实验，并采用主从1:1比例因子。操作员手持MTMR生成一条随机的空间轨迹作为期望轨迹，同时通过光学跟踪系统测量PSM1在笛卡尔空间中的实际轨迹。

图8给出了命令模式和主从模式下的轨迹跟踪响应。

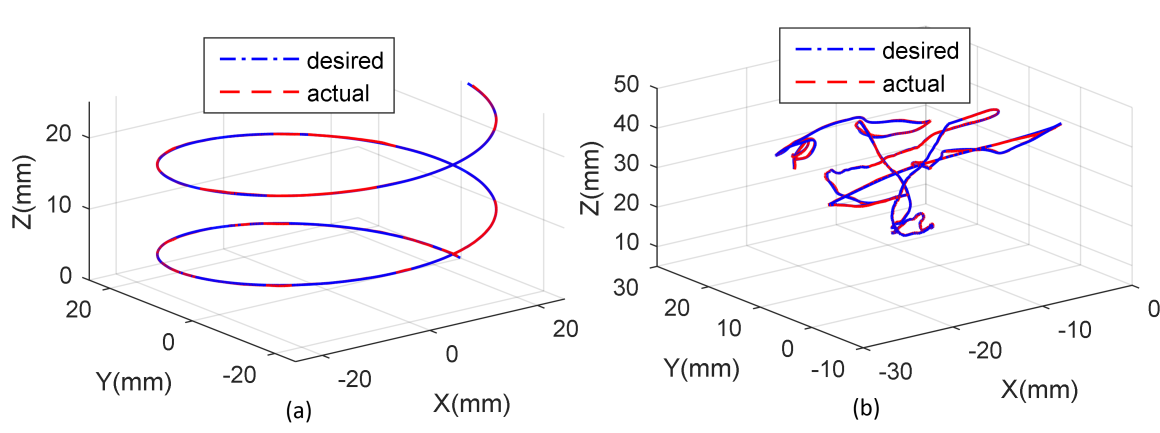
可以看出，在命令模式下，实际轨迹与期望轨迹完全重合，表明配备手术钻孔器械和肌腱传动示意图的PSM1运动学正确，且肌腱张力良好。在主从模式下，实际轨迹几乎与期望轨迹重合，表明主从运动控制正确。

图9还展示了笛卡尔空间三个方向上的主从轨迹跟踪响应与跟踪误差。最大绝对值误差和均方根（RMS）误差见表2。

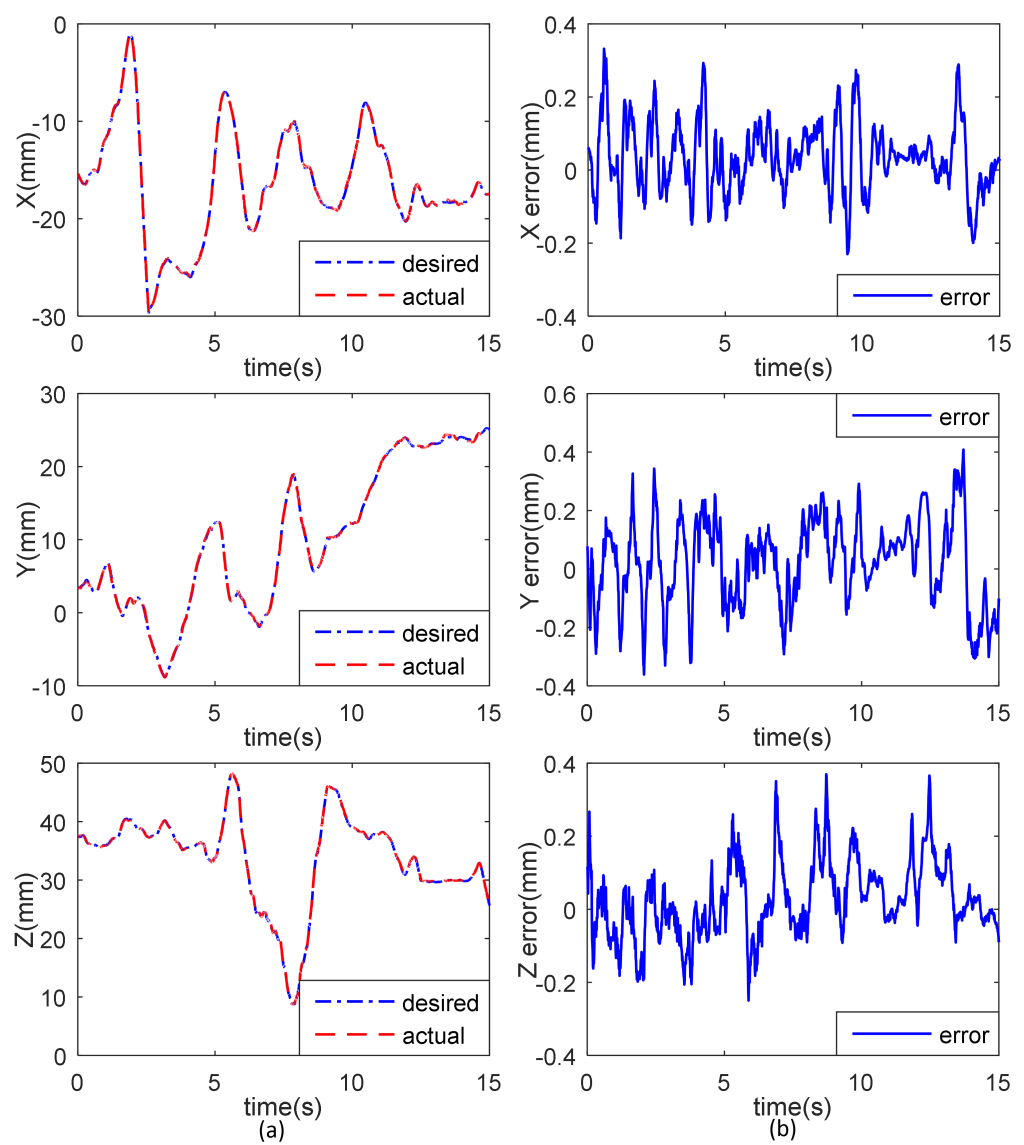轨迹跟踪，(b) 跟踪误差)

表2 PSM1的轨迹跟踪误差

	X（毫米）	Y(毫米)	Z(毫米)	间距(毫米)
RMS	0.1008	0.1482	0.1055	0.2080
MAX	0.3320	0.4084	0.3696	0.4441

从图9和表2可以得出结论，配备手术钻孔器械的PSM1能够实现良好的轨迹跟踪性能和直观运动控制。

5.2 标定实验

根据公式(13)，为了获得钻头的质量和质心以及力和扭矩偏差值，需要在钻头处于自由空间时测量其在世界坐标系中的力和扭矩值以及钻头的姿态。

结合公式(14)和公式(15)，通过在世界坐标系中对手术钻孔器械不同姿态下的力/扭矩传感器测量值进行奇异值分解(SVD)，可获得钻头的质量和质心，以及力和扭矩偏差值。因此，$X_F$和$X_\tau$具有如下形式的解：

$$
X_F = V_F S_F^{-1} U_F^\mathrm{T} F_s \
X_\tau = V_\tau S_\tau^{-1} U_\tau^\mathrm{T} \tau_s
$$

其中，$U_F$、$S_F$、$V_F$和$U_\tau$、$S_\tau$、$V_\tau$是由求解$Y_F$和$Y_\tau$的SVD生成的矩阵。$S_F^{-1}$和$S_\tau^{-1}$分别是矩阵$S_F$和$S_\tau$的伪逆矩阵。

标定时，记录了2600个采样值，这些值在工作空间内均匀分布。采集数据的前半部分用于标定钻头的质量和质心以及力和扭矩偏移。采集数据的后半部分用于评估力和扭矩的标定结果。钻头的质量和质心以及力和扭矩偏移的标定结果见表3。

表3 标定结果

m (kg) 0.0876	x_r(m) 0.0010	r_y (m) 0.0023	r_z(m) -0.0102	F_ox(N) -1.14	F_oy( N) 0.5073	F_oz( N) -0.7198	τ_ox ( Nm) 0.0029	τ_oy( Nm) 0.0187	τ_oz( Nm) 0.0034

重力和力/扭矩零偏补偿后的力和扭矩标定误差如图10所示。表4给出了力和力矩的中位数与最大误差。

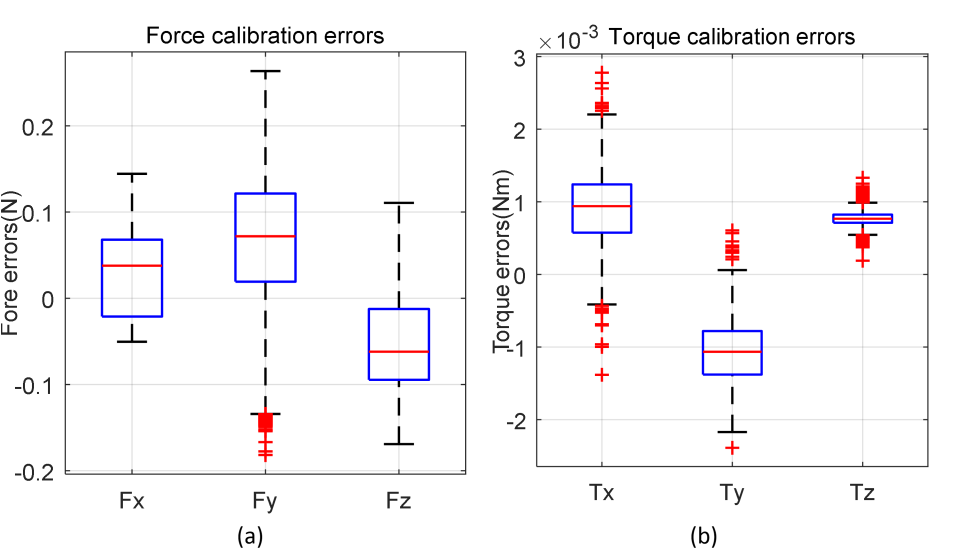力误差，(b) 扭矩误差)

表4 力和力矩的中位数与最大误差

	Fx(N) -0.0378	Fy( N) 0.0719	Fz( N) -0.0619	τx ( Nm) 0.2635	τy( Nm) -0.1691	τz( Nm) 0.0009
中位数
最大值 0.1143

由图10和表4可知，重力和力/扭矩零偏补偿后的力和扭矩标定误差较小，能够满足钻削力反馈要求。

5.3 带有力反馈的钻孔实验

已开发一种实验装置以进行带力反馈的钻孔实验，如图6所示。使用了PHACON颞骨模型。通过力/扭矩传感器测量骨钻手术钻头尖端与骨骼之间的力和扭矩。测得的力和扭矩被转换并补偿到患者侧机械臂PSM1的控制点坐标系中，作为体坐标系下的广义力反馈至MTMR，并在MTMR端转换为关节力矩指令。在开展钻孔实验之前，已在笛卡尔空间的各个方向上验证了主从力变换。在主从模式下，使用钻孔器械对颅骨模型进行扩孔，运动比例因子为5:1，力比例因子为1:1。扩孔过程如图11所示。

MTMR的力和扭矩跟踪响应如图12所示。实际力和力矩是通过实际关节力矩和力雅可比矩阵获得的。表5给出了MTMR的力和力矩跟踪的均方根误差。

表5 MTMR的力和力矩跟踪误差的均方根

	X 力( N) Y 力	( N) Z 力( N)	X 矩( Nm)	Y 矩( Nm) Z 矩	( Nm)
RMS	0.0104	0.0065	0.0125	0.00081	0.00033	0.00029

图11、图12和表5表明，借助力反馈的扩孔任务能够成功完成，且MTMR能够提供准确的力和力矩跟踪性能，进一步证明了力变换的正确性。

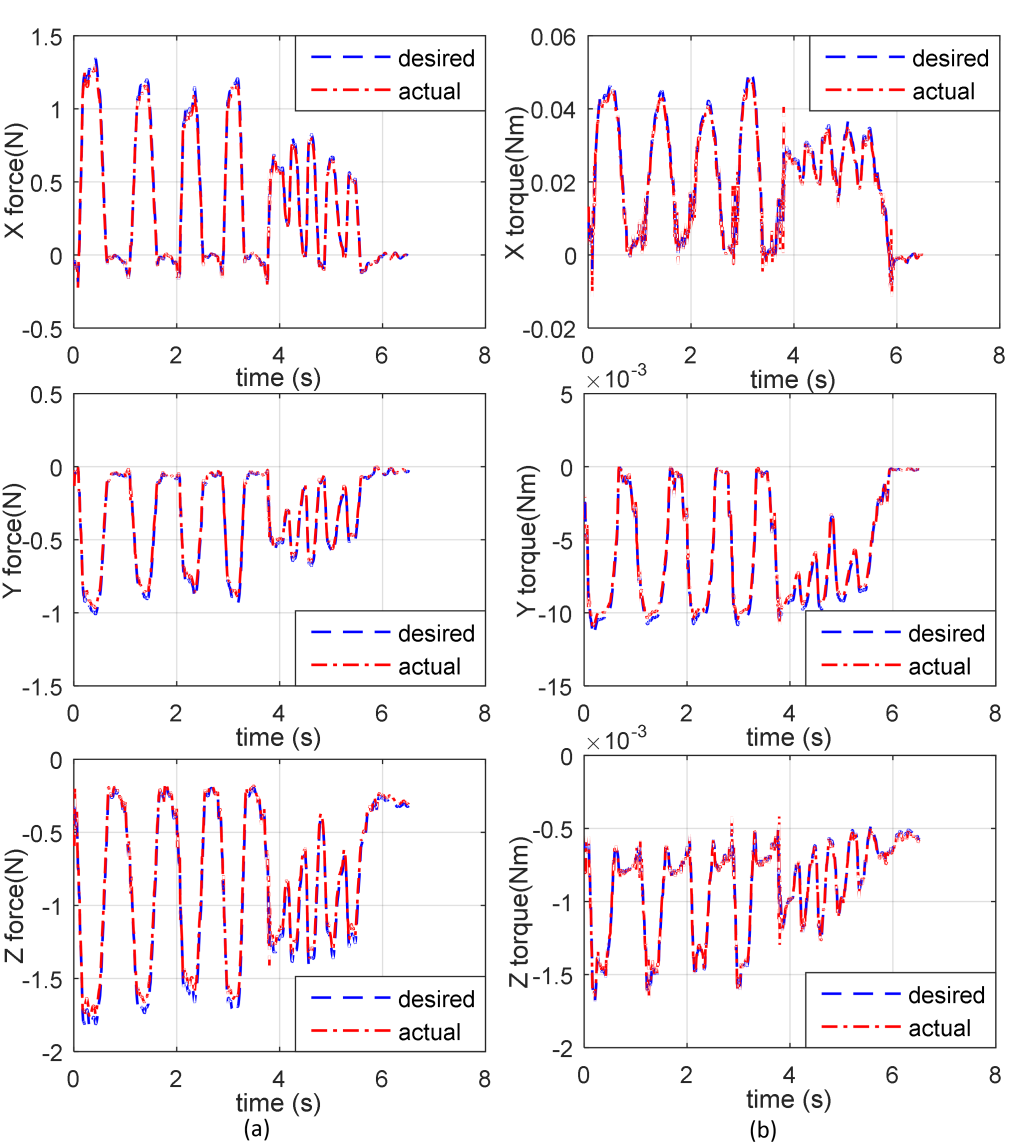扭矩跟踪)

6. 结论

为了研究使用主从式手术机器人系统完成耳鼻喉科手术中钻孔操作的可行性，开发了一种具有力感知功能的改进型达芬奇手术器械。采用改进的DH约定对PSM1的正向运动学进行了分析。通过齐次变换矩阵获得了刀尖偏移变换矩阵。推导了肌腱驱动手术钻具中关节与圆盘之间的位置和扭矩耦合矩阵。基于dVRK实现了带力反馈的控制结构。推导了主从旋转矩阵。为消除由重力的和惯性效应等因素引起的非接触力和扭矩，推导了力和扭矩变换矩阵。通过将传感器坐标系中的力和扭矩变换至控制点坐标系，获取了控制点的力和扭矩信息，并实现了力反馈。

轨迹跟踪实验、标定实验以及带力反馈的钻孔实验已设计并实现。轨迹跟踪实验的结果表明，运动学的PSM1和主从运动控制正确，主从轨迹跟踪具有良好的跟踪性能。通过力/扭矩传感器在世界坐标系中测得的手术钻孔器械的姿态，获得了钻头的质量和质心以及力和扭矩偏差值。对标定结果进行评估后表明，在重力和力/扭矩零偏补偿后，力和扭矩标定误差较小，能够满足钻削力反馈要求。带力反馈的钻孔实验结果表明，带力反馈的钻孔任务可成功实现，并且在MTMR端表现出优异的力和扭矩跟踪性能。

总之，尽管我们的工作展示了该方法的可行性，但仍需进行更多研究，包括在不同操作员和不同骨骼条件下评估钻头性能。此外，还需进一步研究力反馈下的稳定性和透明性。通过使用更轻便的电动钻头，机械系统也有望得到改进。随着这些改进，未来有望实现用于骨骼钻孔的主从式手术机器人系统。