【GAMES101 作业4】贝塞尔曲线+反走样

最新推荐文章于 2024-12-21 21:13:02 发布
原创 最新推荐文章于 2024-12-21 21:13:02 发布 · 1.3k 阅读 · 3 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#c++ #图形渲染

本文详细解读了GAMES101课程中的贝塞尔曲线作业，包括naive_bezier函数的原理与实现，介绍了recursive_bezier和bezier两个函数，并探讨了反走样技术的应用，展示了不同函数和反走样效果的实际效果图。

一、样例函数naive_bezier解读

 

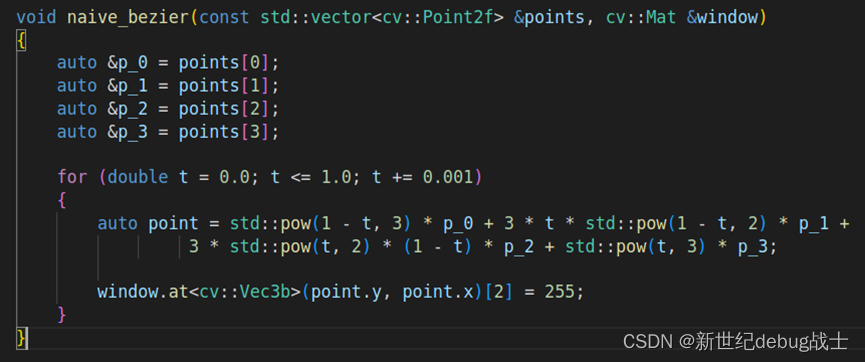
函数名为“简单贝塞尔曲线”。

传入的参数有2，其中：

const std::vector<cv::Point2f> &points：传入points数组，类型是由4个cv::Point2f（用(x,y)表示的点位置，二维数组，float）组成的std::vector类型。

另一个参数是opencv的窗口window。

接下来是对[0,1]内t的遍历，每次增加量Δt = 0.001，公式为lecture11 PPT中4个点的插值公式：

 样例函数的效果如下：

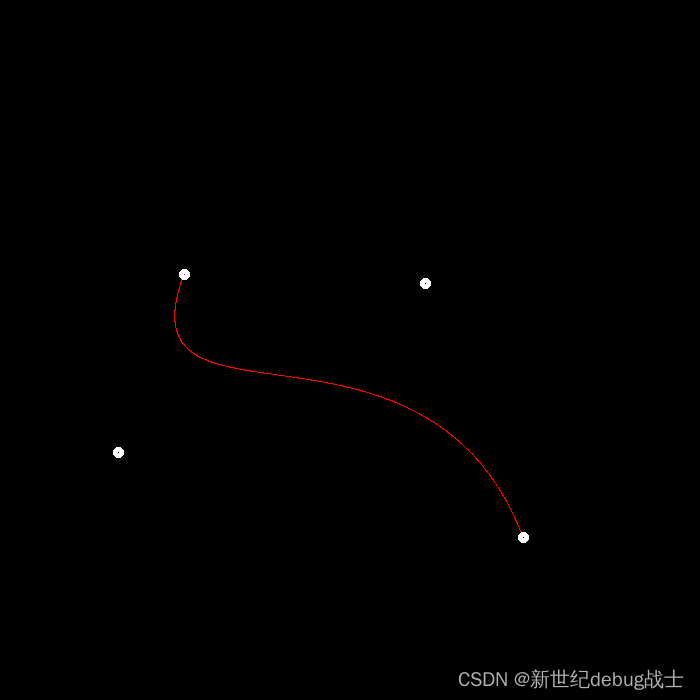
&nbs

最低0.47元/天 解锁文章
Games101：作业4解析（含提高部分）
Q_pril的博客
03-29 7590
目录 作业要求： 1、总览 2、算法 具体代码实现： 提高部分： 参考链接： 作业要求： 1、总览 Bézier 曲线是一种用于计算机图形学的参数曲线。在本次作业中，你需要实现 de Casteljau 算法来绘制由 4 个控制点表示的 Bézier 曲线 (当你正确实现该算法时，你可以支持绘制由更多点来控制的 Bézier 曲线)。你需要修改的函数在提供的 main.cpp 文件中。 • bezier：该函数实现绘制 Bézier 曲线的功能。它使用一个控制点序列和一个Ope
GAMES101-现代计算机图形学学习笔记（作业04）
qq_36242312的博客
03-18 1235
GAMES101-现代计算机图形学学习笔记（作业04） Assignment 04GAMES101-现代计算机图形学学习笔记（作业04）作业作业描述思路 原课程视频链接以及官网 b站视频链接: link. 课程官网链接: link. 作业 作业描述 BeˊzierBézierBeˊzier 曲线是一种用于计算机图形学的参数曲线。在本次作业中，你需要实 现 deCasteljaude CasteljaudeCasteljau 算法来绘制由 4 个控制点表示的 Bézier 曲线 (当你正确实现该 算法时，你可
mfc bezier曲线 反走样
03-09
bezier曲线，反走样处理，曲线很漂亮。曲线可以设置颜色。算法有点一般。运行速度有点慢（反走样的原因）。只做了一次二次和三次曲线，参考一下就行，不是很完美。请用vs2010打开
【GAMES101】作业4（提高）含Bazier曲线的反走样处理
04-14
【GAMES101】作业4（提高）含Bazier曲线的反走样处理
GAMES101-ASSIGNMENT4（作业4）
dx1313113的博客
08-01 1222
对于每个需要计算的t，将调用另一个函数recursive_bezier，然后该函数将返回在Bézier曲线上t处的点。程序将等待你在窗口中选择4个控制点，然后它将根据你选择的控制点来自动绘制Bézier曲线。在本次作业中，你需要实现deCasteljau算法来绘制由4个控制点表示的Bézier曲线(当你正确实现该算法时，你可以支持绘制由更多点来控制的Bézier曲线)。使用[0,1]中的多个不同的t来执行上述算法，你就能得到相应的Bézier曲线。...
Games101-几何（曲线与曲面
Mhypnos的博客
04-08 1157
Games101学习笔记
games101作业4 记录
最新发布
llxllx6969的博客
12-21 1035
美丽的 Bézier 曲线
games101 作业4
weixin_43789369的博客
10-02 840
games101，作业4，贝塞尔曲线
games101，作业4
Elsa的迷弟
12-18 414
最简单的作业，没有之一。 De Casteljau 算法（德卡斯特里奥算法） 一个很简单的递归算法。 数学子领域数值分析中的德卡斯特里奥算法（De Casteljau’s algorithm），以发明者保尔·德·卡斯特里奥命名，是计算伯恩斯坦形式的多项式或贝济埃曲线的递归方法。虽然对于大部分的体系结构，该算法和直接方法相比较慢，但它在数值上更为稳定。 代码 bezier函数控制每一个t参数。 recursive_bezier函数对每一个t递归计算t点的坐标。 cv::Point2f recursive_
GAMES101:作业4
qq_41765657的博客
12-07 5235
GAMES101:作业4 光栅化结束了，下面进入了Geometry的部分。任务是画贝塞尔曲线： 首先什么都不用改，直接运行一下框架查看有无问题： 可以看到运行结果一切正常，接下来开始完成作业。 按照要求：“注释掉 main函数中 while 循环内调用 naive_bezier 函数的行，并取消对 bezier 函数的注释。要求你的实现将 Bézier 曲线绘制为绿色。” naive_bezier里面是代数方法，作业希望我们用De Casteljau算法来实现，也就是通过递归的方式。实际上是非常简单的递归
[Games101 作业4]贝塞尔曲线及反走样
m0_69107096的博客
11-30 372
实现贝塞尔曲线及通过反走样使曲线更加丝滑
GAMES101-现代计算机图形学学习笔记（5）作业4
糯米
08-01 1972
前言 上篇作业3 本篇继续更新作业4相关内容 作业4相关链接 games的作业4链接 我的源码 作业4简述 实现贝塞尔曲线 （提高）对贝塞尔曲线实现反走样 作业4相关知识笔记 贝塞尔曲线相关 作业4思路 此处我考虑的是迭代。 cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t) { // TODO: Implement de Casteljau's al
OPENGL在屏幕上绘制2个点，右边一个蓝色的点，采用反走样技术，左边一个红色的点，不采用反走样技术。比较两个点的区别。
qq_52646857的博客
04-26 322
#define GLUT_DISABLE_ATEXIT_HACK #include<windows.h> #include <gl/glut.h> float angle = 0; //初始化OpenGL int choose = 1; void init(void) { glClearColor(1.0f, 1.0f, 0.0f, 0.0f);//设置背景颜色 glShadeModel(GL_SMOOTH);//设置明暗处理,有两种选择模式：GL_FLAT（不渐变）和GL_.
games 101 作业4
小灰灰的博客
05-26 954
games101 的第四次作业
GAMES101 作业4(贝塞尔曲线推导)
m0_53161412的博客
03-05 561
贝塞尔曲线的推导以及在代码中用递归的方式实现贝塞尔曲线
GAMES101 作业4 贝塞尔曲线 (Bézier Curve)
一名蒟蒻oier的博客
09-29 490
具体代码: #include <chrono> #include <iostream> #include <opencv2/opencv.hpp> std::vector<cv::Point2f> control_points; void mouse_handler(int event, int x, int y, int flags, void *userdata) { if (event == cv::EVENT_LBUTTONDOWN &a
GAMES101-计算机图形学-作业4
qq_40297109的博客
05-05 462
要求： Bézier 曲线是一种用于计算机图形学的参数曲线。在本次作业中，你需要实 现de Casteljau 算法来绘制由4 个控制点表示的Bézier 曲线(当你正确实现该 算法时，你可以支持绘制由更多点来控制的Bézier 曲线)。 你需要修改的函数在提供的main.cpp 文件中。 • bezier：该函数实现绘制Bézier 曲线的功能。它使用一个控制点序列和一个 OpenCV：：Mat 对象作为输入，没有返回值。它会使t 在0 到1 的范围内进 行迭代，并在每次迭代中使t 增加一个微小值。对于每
GAMES101 闫令琪图形学 作业4
再学一个就睡的博客
03-28 568
作业3 问题描述 for (double t = 0.0; t <= 1.0; t += 0.001) { auto point = recursive_bezier(control_points,t); window.at<cv::Vec3b>(point.y, point.x)[1] = 255; } 递归算法 if (control_points.size() == 2) return t * control
贝塞尔曲线+翻页效果
11-23
贝塞尔曲线是一种数学曲线，它可以用来描述平滑的曲线路径。在计算机图形学中，贝塞尔曲线被广泛应用于图形设计和动画制作中。而翻页效果则是一种常见的页面切换效果，可以通过贝塞尔曲线来实现平滑的过渡效果。 ...
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值