基于S-T图的自动驾驶速度规划

动态城市驾驶场景中的自动驾驶速度规划

摘要

在动态交通环境中，轨迹规划对自动驾驶汽车至关重要。通常采用分层方法将其分解为路径规划和速度规划。本文提出了一种在由轨迹规划器定义的路径上进行速度曲线规划的方法，相关信息通过车对车（V2V）通信获取。首先，提出了一种考虑安全性、时间效率、平滑性和舒适性约束的速度规划优化算法。该策略能够在复杂交通环境下，基于S-T图生成安全、舒适且可行的速度曲线，用于自动驾驶。其次，将传统的非凸优化问题转化为二次规划问题，利用CFS（凸可行集）算法显著降低了计算需求。通过在多种城市驾驶场景下的仿真研究验证了所提方案的有效性。这种整体方法为速度与轨迹规划提供了更有效的解决方案。

关键词 —速度规划，S-T图，CFS，二次规划

一. 引言

作为智能交通系统的重要组成部分，速度规划在自动驾驶的轨迹规划中起着至关重要的作用，可确保乘坐舒适性和车辆安全。目前已报道了两种类型的速度规划方法：耦合速度规划和解耦速度规划。耦合速度规划通常应用于运动规划框架中，通过优化技术或搜索策略利用时空空间。McNaughton等人提出了一种在结构化环境中使用时空空间的运动规划器，他们通过考虑空间和时间维度来探索搜索算法。Ziegler等人采用结合构型空间和时间生成的几何图，以应对动态道路驾驶场景中的移动障碍物。Phillips等人构建了一个四维搜索空间（x, y, θ, 时间），其状态由A*算法和安全间隔定义。然而，这些方法在复杂动态环境中因高计算需求而难以实现实时执行。

解耦速度规划方法由于其在降低计算复杂度方面的优势，常用于分层框架中[3]。该策略通过先规划路径，再沿给定路径进行速度规划来分离规划过程。本文的研究重点是后者。在[4],中，基于速度限制和动态物体，利用时空域（S-T域）选择最优速度曲线。该问题通过混合算法求解。然而，该方法可能会影响轨迹的优化。在[5],中，提出了一种沿给定路径具有恒定加速度和速度限制的梯形速度曲线。使用3rd阶多项式进行平滑处理。该方法降低了计算复杂度，但速度曲线并非最优。文献[6]中讨论了一种基于凸优化和时间效率的速度规划方法；然而，该方法未考虑平滑性，这可能导致轨迹性能和安全问题。陈等人提出了一种基于时间优化的低速驾驶场景下的速度规划算法[7]。通过序列二次规划（SQP）对路径上每个节点的时间戳进行优化，并通过安全间隔（SI）定义了安全约束。但在目标函数中未考虑舒适性约束，可能导致收敛后的速度曲线出现突变。为了提高自动驾驶汽车的舒适性，文献[8]展示了一种基于五次贝塞尔曲线、在整个行驶过程中约束全局加速度的新型速度曲线。尽管该方法能够平滑加速度和加速度曲线，但使用五次贝塞尔曲线可能会影响避障结果。因此，为了在动态城市交通环境中获得安全、舒适且可行的速度曲线，本研究提出了一种基于S-T图的速度规划策略。

本文其余部分组织如下。第2节解释了弧长参数化路径与时间参数化速度曲线在S-T图中的关系。第3节基于CFS算法使用二次规划，建立了完成优化问题所需的所有约束的数学表述。第4节提出了仿真结果。第5节给出了结论与未来工作。

II. 问题表述

行为轨迹必须包含自动驾驶汽车的时空信息。本文假设路径生成模块提供了仅包含空间节点的固定路径。为了给每个节点添加时间信息，本节基于S-T图生成速度曲线。该速度曲线是沿路径的时间与距离域之间的一一映射过程，允许在采样点或时间上进行优化。值得注意的是，对于复杂的路径，在采样点上进行优化难以分析和参数化给定路径，该过程可能增加优化复杂度[9]。因此，本研究中的速度规划侧重于时间优化。如前所述，最优速度曲线可通过优化固定路径提供的所有航路点的时间戳获得。速度曲线生成的架构如图1所示。

A. 在S-T图中的速度曲线生成

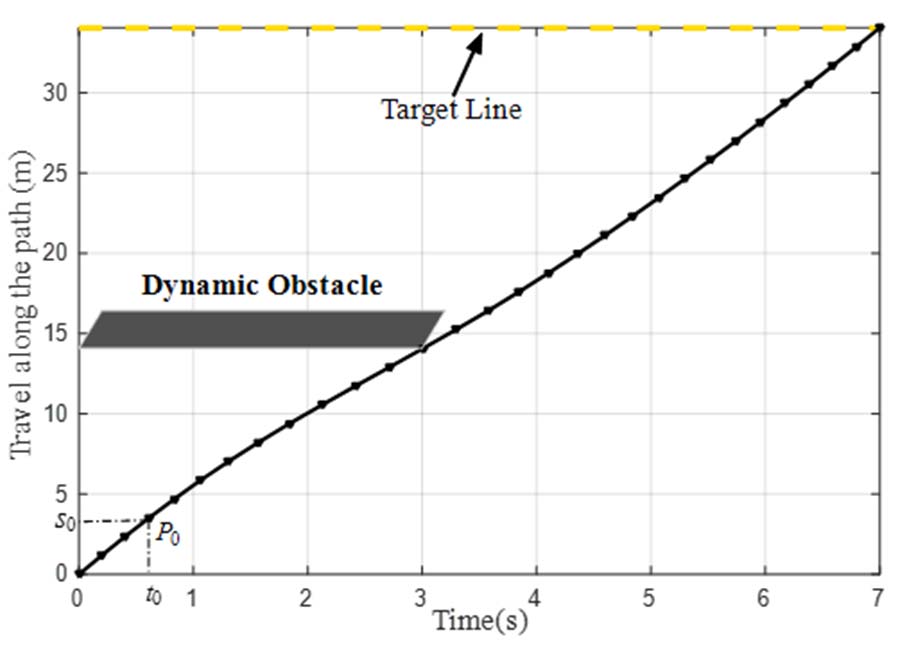
速度规划问题旨在获得一条沿给定路径行驶的安全、高效、平滑且舒适的速度曲线。为解决此问题，本节采用直接优化方法，即根据速度限制和S‐T域中的动态物体生成期望的速度曲线。时空轴分别表示预测时间和沿固定路径的位置。如图2所示，车辆后轴中心的路径表示为 P⊂ R2, ，其为一维尺度，点p0表示在t0,时刻从当前位置起的弧长，记为空间s0, ，其中纵轴为路径的一维参数化，横轴为时间轴。在S‐T域中，动态物体由深色区域标出，而为避免碰撞，速度曲线需在白色区域内生成。速度曲线V等价于S‐T图中的单调曲线。

B. 时间优化

如上所述，速度曲线在S-T图中近似为一条单调曲线（见图2），该曲线定义了每个站点的速度，表示为V = {(Ti, si)}，其中s为沿路径的长度。此外，由于在S-T图中的动态障碍物用于描述移动车辆或行人，若在S-T域中任意两个连续节点之间的距离以及每个节点的时间间隔足够小，则该曲线是无碰撞且平滑的。通过时间轴离散化，可找到路径上每个节点的最优时间戳。参考图3，设pi = p(si)，记pi与pi+1之间的时间间隔为ti = Ti+1 ‐ Ti 。因此，该优化随着时间的推移，确定一系列采样点{si}，并为每个采样点找到所需的时间间隔ti ，其中ti为决策变量。基于此前提，可以在pi （pi= p（si））处确定速度、加速度和加加速度。

$$
v_{i+1} = v_i + a_i t_i + \frac{1}{2} j_i t_i^2 + \frac{1}{3} jerk_i t_i^3
$$

pi处的纵向和横向分别表示为τ(θi)和η(θi)。

时间优化的目标是为每个节点找到最优时间戳，以获得期望的速度曲线。为了确保安全，每个绝对时间戳 Ti 需由上层规划器分配一个时间窗约束。这在图3中有所展示。同时，为了确保速度曲线平滑，从而在避障之外获得更好的性能，车辆还需考虑其他动态约束，例如驾驶质量（如时间效率、速度限制和舒适性）以及可行性（如纵向和横向加速度限制）。因此，可以提出完整的速度规划优化问题（问题1），其表达式如下

$$
\min \sum_{i=0}^{N} w_1 f_{ref} + w_2 f_a + w_3 f_{jerk} + w_4 f_c
$$

s.t

$$
T_i \in U_T = [T_{min}, T_{max}]
$$

$$
a_{\tau min} \leq a_{\tau i} \leq a_{\tau max}
$$

$$
a_{\eta min} \leq a_{\eta i} \leq a_{\eta max}
$$

$$
f_a = a_{\tau i}^2 + a_{\eta i}^2
$$

$$
f_{jerk} = j_{\tau i}^2 + j_{\eta i}^2
$$

$$
f_{ref} = (v_{\tau i} - v_{ref})^2
$$

$$
f_c = \frac{(v_{\tau i} - v_{\tau i-1})^2}{t_i}
$$

其中，公式(2a)是考虑驾驶舒适性和时间效率的目标函数；wi(i = 1, 2, 3, 4)为权重系数；fa和fjerk表示驾驶舒适性；而为了实现纵向和横向舒适性，需分别最小化加速度aτ、加加速度jτ, aη和 jη 。对于时间效率，在不同驾驶场景下需要设定参考纵向速度vτ以指导车辆安全行驶，这由fref表示。需要注意的是，Ti为时间窗约束，Tu> 0表示车辆在时间窗口WT内通过站点si ，从而保证在 域中与其他移动障碍物（车辆或行人）无碰撞。S-T ܽ௜௠௔௫表示加速度限制。最后一项fc 为一致性成本，用于减少速度曲线在任意两个连续时间戳之间 图中的快速变化，该平滑过渡可提升驾驶舒适性[10]。

III. 基于CFS的凸优化问题

为了高效地简化问题1，该问题在CFS算法[11]的框架下被转化为一组二次规划。

A. 重新整理问题

由于车辆的速度、加速度和加加速度在S-T图上呈非线性关系，该优化问题仍然是非线性和非凸的。因此，定义 t=[t1,···, th], ݒ௜௖= ௩೔ೝశ భ௧೔ି௩೔ೝ , ui=[ܽ௜ఛ, ܽ௜ఎ, ݆௜ఛ, ݆௜ఎ, ݒ௜௖,ݒ௥ −ݒ௜ఛ], 和 u= u1,,uh [ ···].

公式(2)的表达式可以表示为

$$
\text{Minimize } u^T R u
$$

s.t.

$$
At \leq b
$$

$$
a_{\tau i}^- \leq u_i \leq a_{\tau i}^+
$$

$$
a_{\eta i}^- \leq u_i \leq a_{\eta i}^+
$$

$$
f_j(t) + g_j(t) u = 0, \forall i,j
$$

其中，公式(3a)是二次规划中的目标函数，R = diag (w1, w2, w3, w4, w5, w6, w1,⋯, w6)，(3b)表示时间窗约束，(3c)表示加速度限制，其与驾驶舒适性相关，单位为 m/s² 和 m/s²。进一步：

$$
A = \begin{bmatrix}
1 & 0 & \cdots & 0 \
0 & 1 & \cdots & 0 \
\vdots & \vdots & \ddots & \vdots \
0 & 0 & \cdots & 1 \
-1 & -1 & \cdots & -1
\end{bmatrix},
b = \begin{bmatrix}
T_{max} \
T_{max} \
\vdots \
T_{max} \
-T_{min}
\end{bmatrix}
$$

此外，公式(1)可以重写为以下表达式，进而成为公式(4)中的函数：

$$
g_i(t) = \begin{bmatrix}
\frac{dp_i^\tau}{t_i} + \frac{dp_i^\tau}{t_i^2}(t_i - t_{i-1}) + \cdots \
\frac{dp_i^\eta}{t_i} + \frac{dp_i^\eta}{t_i^2}(t_i - t_{i-1}) + \cdots \
\vdots \
f_j(t)
\end{bmatrix}
$$

其中dpi= pi+1 ‐ pi，且݀݌௜ఛ和݀݌௜ఎ分别表示为纵向和横向的dpi 。݃௜௝表示݃௜௝中的j th项。此外，通过为所有 i和j. 定义݃௜௝ ≥0 ，可将(3d)和(3e)设计为采用CFS算法的优化问题。

B. 使用CFS算法的二次近似

CFS算法通常用于处理凸成本函数和非线性等式约束问题。本节采用CFS算法来简化公式(3)的计算。第一步是将非线性等式约束松弛为一组非退化的非线性不等式约束。由于(3)在目标函数(3a)和可行性约束(3b)中关于u是对称的，因此可通过线性化(3d)将ݔ ≥ |ݑ| 定义为松弛变量。第二步是使用二次规划序列对松弛问题进行近似。因此，本节提出的近似二次规划可重新整理如下：

$$
\text{Minimize } x^T R x
$$

s.t.

$$
At \leq b
$$

$$
a_{\tau i}^- \leq x_i \leq a_{\tau i}^+
$$

$$
a_{\eta i}^- \leq x_i \leq a_{\eta i}^+
$$

$$
f_j(t^{(k)}) + \nabla f_j(t^{(k)})^T (t - t^{(k)}) + \nabla g_j(t^{(k)})^T x \geq 0
$$

$$
f_j(t^{(k)}) - \nabla f_j(t^{(k)})^T (t - t^{(k)}) - \nabla g_j(t^{(k)})^T x \leq 0
$$

$$
x = [g_j(t^{(k)})]^{-1} f_j(t^{(k)})
$$

注意，公式(3)在特定条件下等价于公式(4)，即如果to是公式(3)的局部最优解，则(to, xo)是在(ݔ௜௝)ᵒ= ቚൣ݃௜௝൫ݐ(௢)൯൧ିଵ݂௜௝൫ݐ(௢)൯ቚ条件下的公式(4)的局部最优解。这一点在[13]中已被证明。此外，该二次规划问题可采用迭代方式求解。假设在第kth次迭代时解t(k)和x(k)可以收敛，则在第(k+1)th次迭代时，(4d)和(4e)关于t(k)和x(k) 是凸的。因此，迭代阈值ߝ可定义为t(k)与t(k+1)之间的差值。这意味着，如果迭代阈值ߝ足够小，即 −ߝ< ݐ(௞ାଵ) −ݐ(௞)< ߝ，则可通过CFS算法迭代收敛求得公式(4)的解。此时根据定义有t( k+1 )= t(o)和x( k+1 )= x(o) 。在开始迭代前，需分别初始化t( 0 )和x( 0 ) ，其设计形式可为 ݐ௜⁰= ௗ௣೔ഓ೔ ௩₀ഓ ，即公式(4)中的(ݔ௜௝)⁰= ቚൣ݃௜௝൫ݐ(⁰)൯൧ ିଵ݂௜௝൫ݐ(⁰)൯ቚ 。

如上所述，当考虑多个约束时，公式(2)可利用CFS近似为一个二次规划序列问题，如公式(4)所示，从而简化计算并降低计算复杂度。

IV. 仿真

为了评估所提出框架的性能，使用英特尔酷睿i7在 MATLAB中通过多个仿真场景实现了所述方法。在本节中，公式（4）中的权重系数，即w1, w2, w3, w4, w5, w6,分别设置为10、0.6、4、0.6、10和1。由于求解二次规划问题的过程与序列二次规划类似，因此通过与 SQP的结果对比来展示CFS算法的效率。当迭代步长小于阈值时，CFS算法和SQP算法均会终止。该迭代阈值在所有三种情况下均定义为 10-4 。此外，每次迭代后的速度曲线或S-T图以灰度显示。需要注意的是，本文提出的方法是在MATLAB中执行的，而非C++或Julia语言等高效率语言，因此计算时间仅用于三种情况之间的比较，但仍可证明所提策略的有效性。

A. 在弯道上应对行人乱穿马路

该场景如图4所示，其中自动驾驶车辆在一条弯道上行驶，在特定时间窗口 [t1= 2s, t2= 3.5s],内，通过车对车通信得知某移动障碍物（车辆或行人）占据了路径上的某一区段，位置为 s= 17 m。如果自动驾驶车辆在不采用所提策略的情况下沿路径行驶，则可能发生事故（见图5中的原始速度曲线）。为安全避开该移动障碍物（车辆或行人），可采用两种策略来避免此问题，如图5所示。第一种策略是在障碍物到达点A之前通过潜在碰撞区域，即Ts=17m<= t1, ，如图5中的蓝色曲线所示。第二种策略是在移动障碍物通过点B之后再通过潜在碰撞区域，即Ts=17m>= t2, ，如图5中的黑色曲线所示。三种不同策略下到达目标线s = 35 m的准确时间分别为3秒、5.8秒和6秒。需要注意的是，具体采用哪种策略由高层规划器判断。考虑到第一种策略可能因受到动态约束而无法高效执行，因此本例中采用第二种策略[12]。

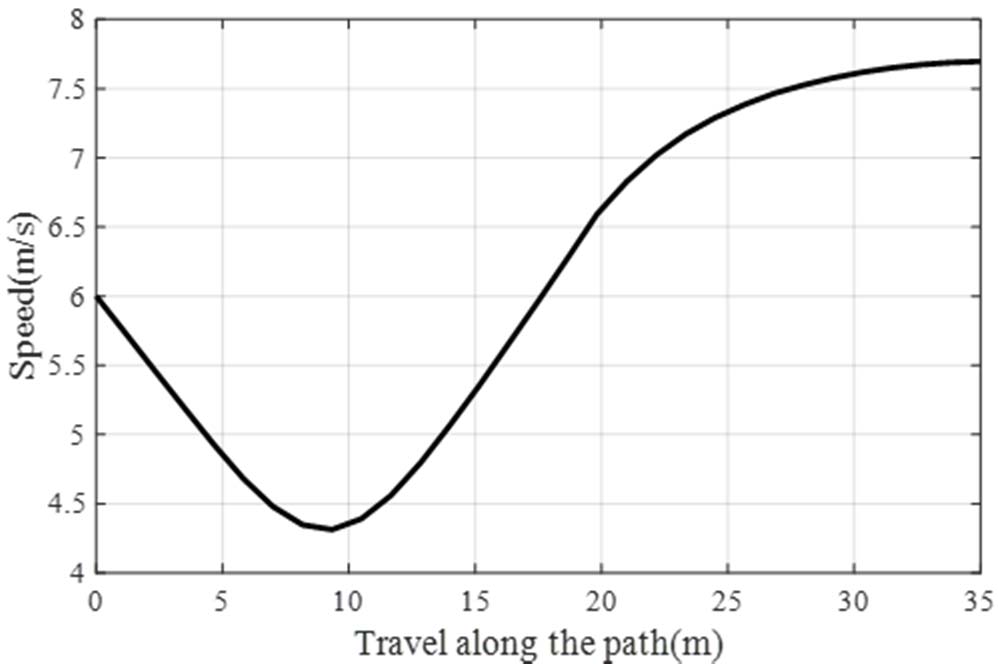
对于安全约束，自车必须在时刻 t1,之前减速，然后由于参考速度的作用，在 t2之后加速。在此情况下，参考速度为 vτ= 8 m/s。初速度为 ݒ଴୰= 5m/s。时间窗口 [Tmin = 0 s, Tmax = 6 s]由高层规划器给出。因此，沿给定路径的最优速度曲线如图6(a)所示，使用CFS求解得到的速度曲线在6次迭代后收敛，如图6(b)所示，总计算时间为 0.24秒。经过80次迭代，SQP算法收敛到相同的速度曲线，总计算时间为8.23秒。

(a) 最优速度曲线
(b) 不同迭代次数下的结果

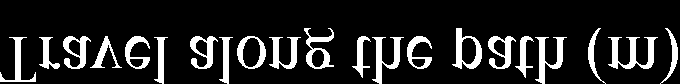
B. 交叉口处的速度曲线

图7展示了一个交叉路口的场景。自动驾驶车辆试图右转进入右车道。与此同时，一名行人正在过马路，灰色车辆即将进入该冲突区域。如果不考虑安全约束，自动驾驶车辆可能会与行人或对向驶来的灰色车辆发生潜在碰撞。为了安全通过该潜在碰撞区域，车辆必须先减速以避让行人，然后在灰色车辆进入潜在碰撞区域之前加速驶离。在此情况下，参考速度为vτ= 6 m/s，车辆初始速度为 ݒ଴୰= 5 m/s。由于灰色车辆和行人占据了路径上s= 15 m的位置，车辆必须在经过点A之后进入潜在碰撞区域，并在到达点B之前通过该区域。此处的时间窗口被限制在 T = 5到6秒之间，即5秒 ≤ ts=15 ≤ 6秒，由V2V通信模块提供。对应的S-T图如图8(a)所示；对向车辆和行人的轨迹在图8(a)中以灰色区域表示。最优速度曲线如图8(b)所示。车辆先减速再加速以避让障碍物。

(a) 交叉路口场景的S-T图
(b) 最优速度曲线

CFS算法在S-T图中的收敛结果如图9所示。第一次迭代的速度曲线是未考虑安全约束的速度曲线，最优速度曲线在3次迭代后收敛，计算时间为0.214秒。作为对比，SQP算法在61次迭代后收敛至相同的速度曲线，总计算时间为7.42秒。

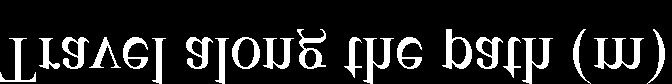
C. 超车速度曲线

图10展示了使用对向车道的超车场景。在此情况下，参考速度为vr= 9 m/s。车辆初始速度为ݒ଴୰= 8 m/s，慢速前车速度为v= 6 m/s，对向车道中对向来车速度为参考速度vτ= 9 m/s。慢速前车的时间窗口t1<= 2.36 s在s = 18 m处被占据，而对向车道车辆的时间窗口t2>= 5.61 s在s = 50 m处受到限制。对应的S-T图如图11所示，其中慢速前车和对向车道中的对向来车以灰色区域表示。图11显示，在无安全约束的情况下，自车可能与其他车辆发生碰撞（图11中的红色曲线）。为确保安全，自车首先因原车道内的慢速前车而减速，随后切换到对向车道并加速完成对慢车的超越，并在对向车道中的对向来车进入潜在碰撞区域之前返回原车道。最优速度曲线如图12(a)所示。

在此场景中，自车减速至点A，即ts= 18m ≥ 2.36 s，然后加速至点B，即ts= 50m ≤ 5.61 s，从而保持两车之间的安全距离。CFS算法在 图中的收敛结果和速度曲线分别如图12(b)和图13所示。收敛发生在6次迭代和0.52秒时。相比之下，SQP算法和CFS算法生成的速度曲线如图14所示。值得一提的是，SQP算法经过86次迭代后收敛到相同的速度曲线，计算时间为9.74秒。

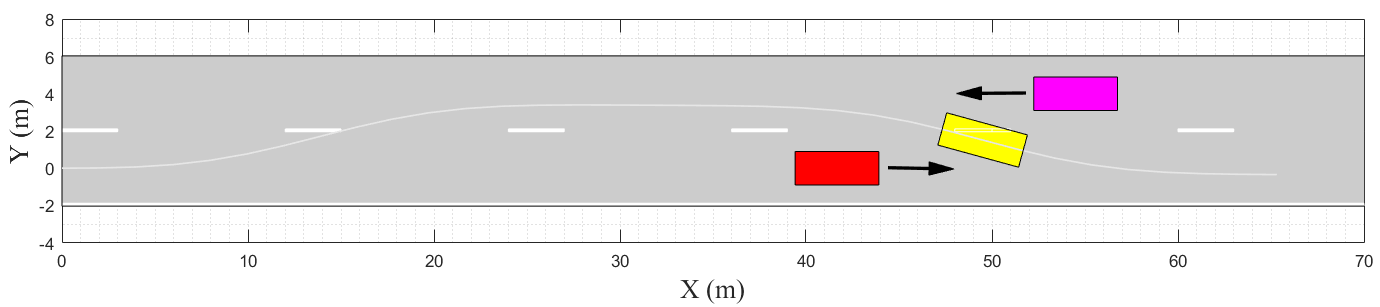
此外，使用MATLAB自动驾驶工具箱和最优速度曲线重建了超车场景。黄色矩形表示自动驾驶车辆，红色矩形表示慢速前车，紫色矩形表示相邻车道的车辆。该车辆在不同时刻的表现如图15所示。

(a) 最优速度曲线
(b) 不同迭代次数下的结果

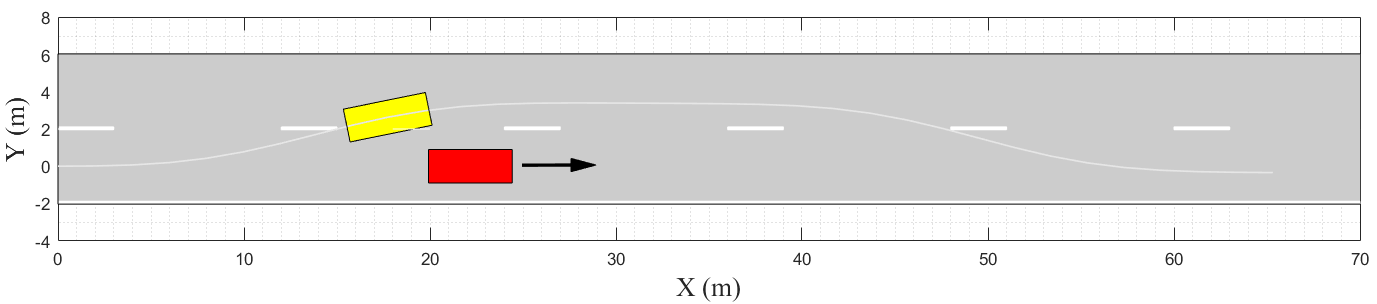
(a) T = 0.52 秒
(b) T = 2.36 秒
(c) T = 5.61 秒
(d) T = 6.86 秒

V. 结论与未来工作

本研究提出了一种基于S-T图的速度规划框架，以获得安全、可行且时间效率高的速度曲线。值得注意的是，本文中对沿路径的一系列航路点的时间戳进行了优化，以执行速度规划过程。为了提高计算效率，利用CFS（凸可行集）算法将传统的优化问题近似为二次规划问题，该方法还满足车辆安全、舒适性和时间效率等多种约束。进行了多个仿真以验证所提出框架的有效性。

未来将考虑紧急停车的终端状态约束，以避免交通环境不确定性导致的潜在碰撞。速度规划计算过程的优化将持续进行，以在实时性和计算成本之间实现更好的平衡。