树莓派与sbRIO9632通信研究

驱动器sbRIO9632与树莓派3之间通信的研究

摘要

本文旨在分析树莓派3与配备sbRIO9632驱动器的移动机器人Starter Kit 2.0之间的通信。设备间的数据传输通过TCP/IP协议实现。第一章讨论了与图像中对象识别算法运行时间相关的课题。随后介绍了测量系统以及TCP/IP协议的描述。接着确定了测试树莓派3与移动机器人之间连接的方法。选用TCP/IP协议作为数据交换方式，并建立了服务器和通信客户端。采用两次时间测量来诊断TCP/IP连接：第一次计时从摄像头获取图像开始，经过数字图像处理，到向服务器发送数据并收到响应为止；第二次计时测量通信时间（发送数据包至收到响应）。时间测量在两种情况下进行：通过网线通信和使用路由器（无线通信）。本文最后一章为结果分析与结论。

1. 引言

在机器人技术中，算法识别物体所需的时间及其有效性对程序员而言最为重要。本文介绍了对处理时间的测量：包括算法以及通过所研究的网络协议发送数据。第一个系统由MS Kinect传感器和树莓派3组成，负责执行与图像处理相关的算法。第二个系统是包含sbRIO9632驱动器的Starter Kit 2.0移动机器人，用于执行操作控制。

硬件分析表明，所介绍的两个设备必须相互通信以交换数据。发送和接收数据包可以通过以下方式进行：通过串行端口（UART → MAX232 → RS232 →计算机）通信、TCP/IP协议、MODBUS/TCP。第一种方法不会被分析，因为其数据交换速度远慢于互联网协议。接下来的两种方法在功能上非常相似。机器人控制软件中提供了用于TCP/IP协议的库，因此本文仅研究此通信方法。在确定了数据交换方式后，应考察哪些变量可能影响实验结果。程序的持续时间主要取决于必须执行的算法数量。因此，应该提出问题：RGB图像处理所需的时间是否会比对灰度图像执行相同操作所需的时间长得多？下一个参数是通过TCP/IP协议发送数据的时间。在这种情况下，也可以提出问题：是仅发送通过图像阈值处理、中心矩确定或Viola‐Jones算法→获得的物体在XYZ坐标中的位置，还是发送整个RGB图像或灰度图像，从而对接收单元提出更高的计算能力要求？发送一个字符串（位置）或矩阵（RGB图像）需要多长时间？

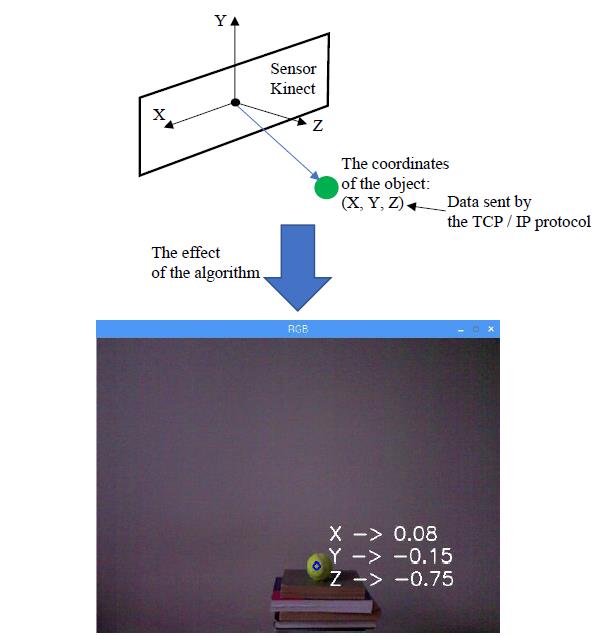
图1展示了Viola‐Jones算法[1]在物体识别与跟踪中的效果。通过该方法，可以获得目标物体的坐标。另一种确定目标物体位置的方法是获取图像后计算其中心矩。在所编写的程序中，采用了后一种方法来生成字符串变量，并通过TCP/IP协议发送至目标设备。

对程序运行时间和通信时间的研究将有助于在移动机器人进行目标跟踪或构建环境地图时，对控制算法进行可能的修正。

TCP/IP 可用于：
- 从管理传感器系统的PLC进行数据采集，以及在虚拟控制器和仿真之间传输数据[2][3]
- 读取工业机器人动态参数的测量结果[4]
- 从控制机器的PLC控制器进行数据采集[5]

2. 测量系统 ‐ TCP/IP协议

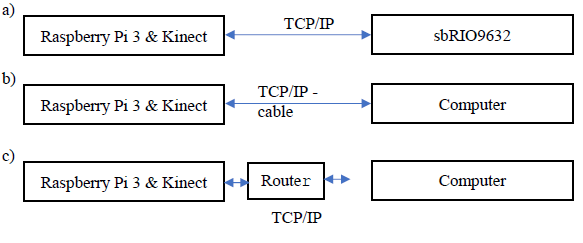
在本文中，考虑了一个由移动机器人Starter Kit 2.0（sbRIO9632驱动器）和树莓派3以及Kinect传感器组成的系统。研究将涉及通过网线连接上述两个控制器，以实现通过TCP/IP协议进行数据传输。在设备附近运行的树莓派3与机器人控制器相连（图2a）。为了采集sbRIO9632的测量数据，计算机被替代。考虑了两种连接类型：使用网线（图2b）和无线路由器（图2c）。

两个控制器中的程序均使用Python的socket库编写，将服务器（sbRIO9632/计算机）的IP地址设置为192.158.1.101，通信端口设置为5005。图3显示了程序[6, 7, 8]的示意图。

程序代码使用了以下库：socket[7], OpenCV[9], NumPy[10], libfreenect[11], time[12]。应用程序的主要元素是执行一百次的WHILE循环。循环中第一行代码将当前循环的开始时间写入变量。然后读取Kinect传感器的信号，并以RGB图像格式和灰度图像保存。随后执行与数字图像处理相关的算法：转换HSV颜色调色板、根据预定义颜色范围对图像进行阈值化处理以及计算中心矩。使用这些方法可以跟踪物体并确定其坐标。在发送变量之前的最后阶段，是将坐标值合并为一个字符串变量。接下来输入启动通信命令，并指定必要的数据交换参数。在传输开始前，将当前时间赋值给参数变量。下一步是将变量编码为字节并发送到服务器。

服务器对发送值的响应会触发当前时间的测量，并减去之前的时间测量值。接收到的时间被保存到矩阵中。在执行完一百次循环后，程序将表格保存为文本格式文件。

计算机所分配的服务器在客户端开始活动之前已连接。管理单元正在等待来自客户的消息。当连接建立后，从设备会发送一个数据包。随后进行解码并生成响应。

该算法的结果是生成一个文件，其中包含单个程序周期以及两个设备之间通信的100次时间测量。所获得的结果将允许对其进行分析，并确定改变任何参数的影响的显著性。

3. 测试结果分析

表1中列出的参数被用于测试。实验结果包括程序周期时间和数据发送。采用两级计划对结果进行分析。两个参数在两个变化水平上被采用。针对每种变量配置都进行了实验。然后，基于[13–17]中描述的数学工具，确定了对象的数学模型。

变量名称	变量符号	波动水平(-)	波动水平(+)
图像(O) x1	灰度 → 640x480	RGB → 640x480x3
已发送元素（E） x2	数字 → 15	图像 → 640x480

变量编码和解码使用单位变化（ui）和变量中值（mi）[13–17]表示：

$$
u_1 = \frac{O_{max} - O_{min}}{2} = \frac{921600 - 307200}{2} = 307200
$$

$$
m_1 = \frac{O_{max} + O_{min}}{2} = \frac{921600 + 307200}{2} = 614400
$$

$$
x_1 = \frac{x_1 - m_1}{u_1} = \frac{O - 614400}{307200}
$$

$$
u_2 = \frac{E_{max} - E_{min}}{2} = \frac{307200 - 15}{2} = 153592.5
$$

$$
m_2 = \frac{E_{max} + E_{min}}{2} = \frac{307200 + 15}{2} = 153607.5
$$

$$
x_2 = \frac{x_2 - m_2}{u_2} = \frac{E - 153607.5}{153592.5}
$$

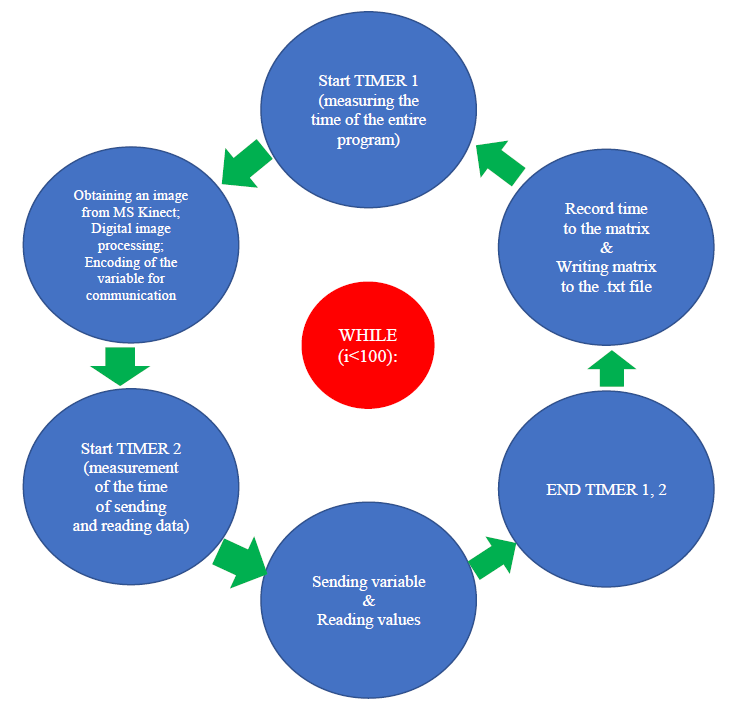
表2显示了两级卫星计划的实验方案，其中：
- $\bar{y} {tpc}$ – 程序运行平均时间（网线）
- $\bar{y} {tcc}$ – 通信平均时间（网线）
- $\bar{y} {tpr}$ – 程序运行平均时间（路由器）
- $\bar{y} {trc}$ – 通信平均时间（路由器）

实验编号	$x_0$	$x_1$	$x_2$	$x_{12}$	$\bar{y}_{tpc}$	$\bar{y}_{tcc}$	$\bar{y}_{tpr}$	$\bar{y}_{trc}$
1	+	+	+	+	43.2318	17.8087	49.0551	19.2336
2	+	+	-	-	41.7152	16.0544	44.1335	17.9611
3	+	-	+	-	36.7627	21.4453	39.2077	24.7019
4	+	-	-	+	31.2379	20.1288	32.1836	20.8447

基于回归方程[13–17]创建数学模型：

a) 一种用于测量平均程序运行时间的系统数学模型——互联网电缆：

$$
t_{pc} = 38.24 + 4.24x_1 + 1.76x_2 - x_1x_2 \quad (7)
$$

解码形式：
$$
t_{pc} = 38.24 + 4.24\left(\frac{O - 614400}{307200}\right) + 1.76\left(\frac{E - 153607.5}{153592.5}\right) - \left(\frac{O - 614400}{307200}\right)\left(\frac{E - 153607.5}{153592.5}\right)
$$

基于t‐学生统计量和显著性水平α=0，对回归方程系数进行显著性检验：
- $b_0$ – 重要系数
- $b_1$ – 重要系数
- $b_2$ – 重要系数
- $b_{12}$ – 重要系数

b) 测量平均通信时间的系统数学模型 ‐ 互联网电缆：

$$
t_{kc} = 18.86 - 1.92x_1 + 0.77x_2 + 0.11x_1x_2 \quad (9)
$$

解码形式：
$$
t_{kc} = 18.86 - 1.92\left(\frac{O - 614400}{307200}\right) + 0.77\left(\frac{E - 153607.5}{153592.5}\right) + 0.11\left(\frac{O - 614400}{307200}\right)\left(\frac{E - 153607.5}{153592.5}\right)
$$

显著性检验结果：
- $b_0$ – 重要系数
- $b_1$ – 重要系数
- $b_2$ – 重要系数
- $b_{12}$ – 系数不重要

c) 用于测量平均程序运行时间的系统数学模型 ‐ 外部（路由器）：

$$
t_{pr} = 20.69 - 2.09x_1 + 1.28x_2 - 0.65x_1x_2 \quad (11)
$$

解码形式：
$$
t_{pr} = 20.69 - 2.09\left(\frac{O - 614400}{307200}\right) + 1.28\left(\frac{E - 153607.5}{153592.5}\right) - 0.65\left(\frac{O - 614400}{307200}\right)\left(\frac{E - 153607.5}{153592.5}\right)
$$

显著性检验（α=0.1）：
- $b_0$ – 重要系数
- $b_1$ – 重要系数
- $b_2$ – 重要系数
- $b_{12}$ – 重要系数

d) 测量平均通信时间的系统 ‐ 路由器的数学模型：

$$
t_{kr} = 41.15 + 5.45x_1 + 2.99x_2 - 0.53x_1x_2 \quad (13)
$$

解码形式：
$$
t_{kr} = 20.69 - 2.09\left(\frac{O - 614400}{307200}\right) + 1.28\left(\frac{E - 153607.5}{153592.5}\right) - 0.65\left(\frac{O - 614400}{307200}\right)\left(\frac{E - 153607.5}{153592.5}\right)
$$

显著性检验（α=0.1）：
- $b_0$ – 重要系数
- $b_1$ – 重要系数
- $b_2$ – 重要系数
- $b_{12}$ – 重要系数

4. 结论

测试共采集了八千个样本。测量了程序持续时间和通信过程。基于两级计划，针对两种连接类型分别为两个时间确定了4个数学模型。结果表明，使用路由器时始终记录到更长的通信时间和程序运行时间。结果之间的差异并不显著，不应影响移动机器人对对象的跟踪。然而，测量是在路由器距离计算机两米以内时进行的。发送数据的时间还将取决于路由器的类型，可能还取决于网线的长度。所进行的研究确定了数字图像处理算法以及通过TCP/IP协议发送的数据包的持续时间。

后续研究阶段将使用树莓派3和Kinect传感器创建点云，然后将3D图像发送到计算机，在计算机上验证接收到的数据。